2009-10-30[n年前へ]
■「京都市鴨川源流」を廻る「理系風デート」 
青春小説のようなシーンを交えながら、数学世界を解説していく「数学ガール
「じゃあー少しだけ、僕とデートしてくれませんか？」
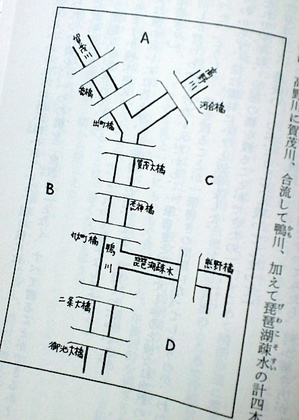鴨川の始まりである出町柳辺りから、御池大橋までを舞台に、オイラーが解いた「ケーニヒストベルグ橋の問題」を題材にして、ローマの休日風な素敵で切ない数時間（と数ヶ月）を描いた一話です。見事なくらいに、微妙な心の機微と数学の世界が一体化した素敵で少し切ない短編です。
午後四時になってもまだ陽の高い、京都の休日へ繰り出した。
実際には、「ケーニヒストベルグ橋の問題」を解くという口実の（体力的に疲れそうな）デートに、付合ってくれる女性は少なそうな気がします。・・・とはいえ、この「京都市鴨川源流」を廻る「理系風デート」の一話、「ローマ風の休日」はとても楽しめる話です。
「ローマ風の休日」は「ホルモー六景
ケーニヒスベルグの橋とは、プロシアの首都ケーニヒスベルグ（現在はロシア領カリーニングラード）を流れるプレーゲル河に架かる7つの橋のことである。この7つの橋を全て一度だけ渡り、元の場所に戻れるか、という議論によって有名となった。
ケーニヒスベルグの橋の問題は1736年に、数学者オイラーにより、地図を線と点で表現し、その図形を一筆書きできるかの問題と整理されて考えられた。その結果、一筆書きできない、すなわちケーニヒスベルグの7つの橋を求められた条件の下に渡る道順は無いとして、解決された。ケーニヒスベルグの橋は、グラフ理論とトポロジーの起源であると言われている。
ケーニヒスベルグの橋
さて、鴨川源流を舞台にした「ケーニヒスベルグの橋の問題」はどのような答えになるでしょうか。ノートの上で手と頭で解いてみても良いですし、京都の街を自転車で走り、この数学の問題を足と体で解いてみると面白いと思います。そんな「理系風デート」があると・・・さらに、楽しいでしょうね。
彼女ははそれから、いろいろな数学の話を聞かせてくれた。
2009-10-31[n年前へ]
■「マンハッタン距離」と「続 理系風デート」
万城目学のエッセイ集「ザ・万歩計
京都の生活には、自転車がよく似合う。いわゆる京都市内、つまり、山あり谷ありではない市内を移動するには、確かに自転車が一番適している。周辺部以外には、曲がりくねった道はなくて、道はすべて真っ直ぐ東<->西か南<->北方向に走っている。だから、どこに向かうにもただ、目的の方向に進み・曲がればいいだけだ。
出発地から目的地まで行くのにかかる時間を見積もる、つまり、出発地から目的地まで行く経路の距離を計算するのだって、とても簡単だ。上に書いたように、平安京の時代からある京都市内中央部は、碁盤の目状に道が配置されている。だから、経路の距離は「マンハッタン距離」で計算することができる。東京の街中なら、不定形の道に沿って線積分する必要があるだろうし、野原の真ん中なら…少しは単純だけれど「ユークリッド距離」を計算するために平方根（ルート）を計算してやらなければいけない。そんな計算は面倒だ。しかし、京都市内は違う。
「京都市内の距離空間はマンハッタン距離で計算できるのがいいね」といった、自転車に乗りながらの理系風会話が日常的にしやすい。もちろん、「マンハッタン」距離なんていう一見オシャレに響く言葉を使っているので、理系風デートで使えなくもないフレーズである。
「目的地までの東西距離と南北距離を足すだけでいいから、計算が簡単でいいよね」
「どの平方根…じゃなかった、ルートでも距離は同じだしね」
しかし、その後に、こういうウンチクを口にし始めてしまったりすると、しかもそれが「理系風デート」ならその時点で「終了」していまうことが多い。
あれ？マンハッタン距離を考えたヘルマン・ミンコフスキーって、機動戦士ガンダムのミノフスキー粒子と関係あるのかな？これで会話が続いたら、単なるガンダムおたくである。まさに、「若さゆえの過ち」「ぼうやだからさ」状態である。
…とにかく、京都の町には自転車が良く似合う。先の万城目学のエッセイ「都大路で立ちこいで」でも、最後の一文はこう終わる。
自転車で京都を走ることが掛け値なしに楽しい、ってことだけは、本当なのだ。京都の町に行くのなら、自転車を借りて市内を散策するのが一番いいと思う。紅葉間近のこの季節、天気の良い日なら、乗りやすいマウンテンバイクでも借りて、体育会風に（できれば2,3日かけて）京都を一周してみるのもいいと思う。それがたとえ、1日だけでも、やはり自転車で京都を走ってみたならば、バスや列車で街を離散的に巡るよりも、ずっと素晴らしく連続的な京都の街を知り・同時に楽しめると思う。
「理系」と「文系」と言った話より、「頭」と「体」とか、「情緒/心/感情」と「論理」といったことの方に、今は魅力と確かさを感じる。自転車で巡る京都の町の魅力はは、少なくとも「体」と「情緒/感情/心」といった辺りの中心部を貫くと思う。
2010-12-11[n年前へ]
■春分と秋分の日には京都に行こう!?
ニューヨーク マンハッタンの街並みは、道路が碁盤の目状に走っています。だから、「道のり」を考えるとき「各座標の差（の絶対値）の総和を2点間の距離とする」というマンハッタン距離を使うことができます。そしてまた、道が格子状に走るマンハッタンでは、5月28日と7月12日の夕暮れには「どの交差点でも道路の先に沈む夕日が見える」のです。もしも、空の上からマンハッタンの街を眺めることができたなら、どの道路にも夕日が奇麗に差し込んで、さぞかし美しい景色が見えるに違いありません。
マンハッタン距離を使うことができる街といえば、京都もそういう街のひとつです。東西南北方向に向けて、碁盤の目状に道が作られています。だから、太陽が真西に沈む春分と秋分の日近辺では、何本もの東西に走る道の向こうから夕日の光が差し込んでくる、ということになります。
「京都市内の距離空間はマンハッタン距離で計算できるのがいいね」「目的地までの東西距離と南北距離を足すだけでいいから、計算が簡単でいいよね」「どの平方根…じゃなかった、ルートでも距離は同じだしね」
「マンハッタン距離」と「続 理系風デート」
もっとも、京都は山に囲まれた箱庭のような街なので、実際に夕陽が沈むのは、それよりも南側になりますし、山並みに隠されて夕日が見えない場所もあるかもしれません。けれど、春分の日と秋分の日近くに、京都の街を上空から眺めたとしたら、美しく光が東西に走る景色が見えるかもしれません。
春分と秋分の日には京都に行って、清水寺や比叡山や大文字山に登り、夕日に照らされた街並みを眺めてみたくなります。京都の人たちは、千二百年の昔から、そんな道の向こうに沈む夕日を眺め続けてきたのでしょうか。
パリやロスにちょっと詳しいより
京都にうんと詳しいほうが
かっこいいかもしれないな。
そうだ 京都、行こう。 1993年 「秋〜清水寺」
2011-02-06[n年前へ]
■街で見かけた「ケーニヒスベルクの橋渡り問題」
「街を流れる川に架かる7つの橋を、一筆書き状にすべて渡り、（どこでも良いから）スタート地点に戻ってくることができるか？」というのは、オイラーが解いた「ケーニヒスベルクの橋渡りの問題」です。ケーニヒスベルクというのは、今はカリーニングラードと呼ばれるバルト海沿いにあるロシアの街です。
この「ケーニヒスベルクの橋渡りの問題」は、私たちの住む街にも、実はたくさんあったりするものです。たとえば、今日頂いた「街で見かけたケーニヒスベルクの橋渡り問題」が下の写真です。看板に描かれた川と、その川にかかる橋群は、まさに「ケーニヒスベルクの問題」です。「鉄道専用らしき橋を渡ることができるとしたら」とか「鉄道専用橋は渡ることができないとしたら」という風に、条件を変えながら眺めてみても面白そうな、そんな「ケーニヒスベルクの看板」に見えます。
あなたの街にも、きっと「ケーニヒスベルクの橋渡り問題」がどこかに隠れているはずです。今日頂いた「ケーニヒスベルクの問題」看板のように、あなたが見つけた、そんな風景（写真）「理系の散歩道」をお裾分けして頂けたら、心からうれしく思います。
2011-02-20[n年前へ]
■次のバス停は「高周波前」!?
「理系の散歩道」…それは、理系人間が街を歩く時に眺める景色です。たとえば、それは都会の川沿いに描かれた「ケーニヒスベルクの橋渡り問題」です。理系という名のメガネをかけた「理系人間」は、川沿いの道を歩く時にも十八世紀頃のバルト海沿いにある街で話題になったというトポロジカルな数学の問題を見い出したりするのです。
今日はこんな「理系の散歩道」を見つけました。バスに乗り、知らない街の景色をもの珍しく眺めていると、「次のバス停は○×△前〜○×△前〜」と、信じられない言葉を聞いたのです。そして、その言葉に驚き思わずバスを飛び降りると、そこにはこんな景色がありました。
バスを降りると、そのバス停看板には「高周波前」と描かれていました。「高周波」ってどのくらいの周波数なんだ!?とか、高周波には「前」とか「後ろ」とかあるのか!?とか、そもそも、「なんで高周波前やねん!?」という「くだらないツッコミ」をひとり呟きつながら、バス停「高周波前」を記念写真に撮りました。それがこの写真です。一体、なぜ「高周波前」なんでしょう。何か変なデンパでも受信しているのでしょうか…？
理系の散歩道…それは、あなたの目の前にある景色です。あなたが見つけた、そんな風景（写真）「理系の散歩道」をお裾分けして頂けたら、心からうれしく思います。
」など。