2000-08-16[n年前へ]
■エアコンの風は心地よく吹くか? 
真夏の夜の夢 流体力学入門編
私は長野県の野辺山という高原で幼い時期を過ごしたせいか、暑さにとても弱い体である。なので、真夏の夜はエアコンが欠かせない体と根性になってしまった。エアコン無しではろくな夢が見られ無いどころか、眠れなかったりするのである。気持ちの良い「真夏の夜の夢」を見るためには、エアコンがとっても重要なのである。
つい先日、そんなエアコンの話題が「今日の必ずトクする一言」に載っていた。それが、
- エアコン用流体素子(PATPEND.)のナゾ
- ( http://www.bekkoame.ne.jp/~jh6bha/higawari.html#000819 )
- 復活する冷蔵庫脱臭剤のナゾ(1/f揺らぎと活性炭編)
- ( http://www.bekkoame.ne.jp/~jh6bha/higawari.html#000901)
(おそらくhiraxさんあたりがやってくれるのではなかろうか)と話題のパスまでされている。いきなり、ボーとしているところを授業で当てられた気分である。
とはいえ、「エアコンの流体力学」というのもちょっと興味のある話題でもあるし、パスされたからにはやってみなければなるまい。そういうわけで、真夏の眠れない夜のパズル代わりに挑戦してみることにした。
さて、部屋の中の「エアコンから送られる風の様子」を計算するということは、流体力学の計算をするということになる。流体力学の運動方程式(ナビエ・ストークス式)に代表されるような方程式群を解かなければならないのである。そこで、以前
の時にいじりかけたMichael Griebel氏らによる非圧縮性流体のNast2Dのコードをもう一度引っ張り出して使ってみることにした。このNast2Dは非圧縮性二次元流れを計算する教育用のソースコードである。詳しくは- TUM INFO V- Homepage - ( http://www5.informatik.tu-muenchen.de/home_us.html )
- Numerical Simulation in Fluid Dynamics A Practical IntroductionISBN 0-89871-398-6
計算するモデルは次の図に示すような部屋である。四畳半一間であるかもしれないし、100畳以上の大きな広間かもしれないが、とにかく正方形の部屋だ。向かって左の青い丸部分にはエアコンがあり、そこから冷たい空気が送られてくるのである。そして、この部屋には何故かタンスがおいてある。「やっぱり、この部屋は四畳半一間じゃないの」というツッコミは言ってはいけない約束である。とりあえず、このタンスが向かって下側にある紫の部分である。このタンスが、エアコンから送られてくる冷た〜い空気流の障害物となるのである。
 |
暑い真夏の夜に、こんな部屋をエアコンで涼しくする時のことを考えてみよう。気持ちよく眠るために、何はともあれエアコンのスイッチを入れるわけだ。そうしないと、暑くて眠れないから当然である。
そして、そのエアコンには送風モードが何故か三つあるのだ。次のような三種類の送風、
- 真っ直ぐ送風するモード
- 単純な首振り送風をするモード
- 山本式エアコン用流体素子を用いた送風をするモード
空気流の速度分布の計算結果を次に示してみよう。
|
| を用いた送風の場合  |
また、これらの場合の計算結果を動画で示したものをMPEG4形式のAVIファイルとReal形式のファイルにしたものを以下に置いておく。エアコンから空気が送られる様子を知るには、何はともあれこの動画を見て頂きたい。なお、手元のRealProducerの制限のために、このReal形式のファイルは古いバージョンのRealPlayerだとアップデートが必要になってしまった。また、MPEG4のCodecが導入されていない場合には、DivXなどをインストールする必要がある。
とりあえず
- 真っ直ぐ送風している場合 MPEG4 AVI ( 289KB ) Real形式( 73KB )
- 単純な首振り送風の場合 MPEG4 AVI ( 577KB ) Real形式( 89KB )
- 山本式エアコン用流体素子を用いた送風の場合 MPEG4 AVI( 693KB ) Real形式 ( 92KB )
また、それぞれのMPEG4形式の動画のファイルサイズを見れば、それぞれの場合の送風による空気流の速度分布の複雑さは一目瞭然である、と思う。真っ直ぐ送風している場合はとにかく単純な速度分布であって動画ファイルサイズも結果的に小さくなっているのに対して、山本式エアコン用流体素子を用いた送風の場合はかなり複雑な速度分布になっていて動画ファイルも結果的に大きくなっているのである。
動画を見ることができない人のために、それぞれの場合の連続した3つの瞬間における部屋内の空気流の速度分布の静止画も示しておく。
1 | 1 | を用いた送風の場合 1  |
 |  |  |
 |  |  |
これを見ると、「真っ直ぐ送風している場合」にはエアコンの正面は強烈に風が当たっている(つまり冷えまくっている)ことがわかるが、タンスの陰になっている部屋の隅などはほとんど空気が動いていないことがわかる。また、「単純な首振り送風の場合」は送風方向を動かしているとはいえ、その送風方向の変化はかなりゆっくりであって部屋の中の空気流の速度分布はそれほど急激には変化していないことも判ると思う(そういう風に計算しただけではあるが...)。いずれにせよ、もしもこの部屋の中にあなたがいたとしたら、体の決まった部分にのみ冷た〜い風があたることになるわけだ。それは体にはちょっとよろしくなさそうである。
一方、「山本式エアコン用流体素子を用いた送風の場合」は時々刻々と送風方向が変化しており、まるで部屋を舐め回すかのように、冷た〜い空気が送られていることがわかると思う。この部屋の中にもしあなたがいたとしても、体のごく一部分だけに冷たい風が当たるようなことはなく、それほど体に悪くないことが予想されるわけである。
さて、このページもかなり重いページになってきた。本来はこのタンスの裏側の空気が澱みやすい場所の「空気の入れ替わり」を、送風の具合を変えた上で調べてみたいわけであるが、それは次回のお楽しみ、ということにしておきたい。とりあえず、「真夏の夜の夢 流体力学入門編」はここら辺で終わりにしたい。
さて、夏休というわけでこんな景色のところで気持ちの良い風に吹かれてみたりするわけである。この写真の先の方の海の向こうに見えているのは左が伊豆半島で、右が三保の松原の辺である。

暑い夏の夜はエアコンが欠かせない体ではあるけれど、気持ちの上で言えばエアコンよりはおんぼろの扇風機の方が好きだし、扇風機よりも山の上の風の方がずっと好きだ。いつか、山の上を吹き抜ける風の音を録音して、その1/f揺らぎでも調べてみようかなと思うのである... それとも、そんなことをしてもツマラナイだけかな?
2000-10-15[n年前へ]
■地平線際の星が見える場所 
「地平線近くの月が大きく見えるのが、比較対象物があるせいならば、何故地平線際の星座は大きく見えないのか」というメールに返事を書く。星座だって本当は大きく見えたりしているのだけれど、気にしたことがなかったり、地平線際の星が見えなかったりするだけではないでしょうか、と書いた。月に比べて普通の星はずっと暗いので、街の中のビルなんかの明かりの近くにあるときっとはっきりと見ることはできないだろう。私がかつて住んでいた長野県の野辺山でも今では山際にスキー場がいくつかあるし、ライトアップされた45m電波望遠鏡もある。きっと、もうあそこでも山際で光る星は見えづらいのだろう。
2001-06-04[n年前へ]
■あなたの声が、すぐそばにある 
高原の向日葵と月見草 編
昨日、東京駅の地下街にある「王様のアイデア」でこんなものを買った。見ての通り、ピストル型の集音マイク"SonicExplorer"だ。その数日前にその集音マイクを初めて見かけたのだが、遊んでみるとどうにも気に入ってしまって、次に見た時には必ず買おうと決めていたのである。
 |
数日前に、その"Sonic Explorer"を見かけた時は出張帰りだったのだが、地下街の雑踏の中で「頭にヘッドホンを被り、ゴルゴ13のように集音ガンで狙っている」様子はさぞかしアブナイ奴に見えたに違いない。現に、私が雑踏の中に"SonicExplorer"で狙いをつけていたときには、一緒に出張していた仲間が二・三歩後ずさりして、私の側から離れていったくらいである。自分でも怪しい姿だとは思ったのだが、そんなことを忘れてしまうくらいに面白かったのである。こんなおもちゃみたいな外見に似合わないほど、これを使うと遠くの音がピンポイントでよく聞こえるのだ。地下街の雑踏の中で遥か向こうで携帯電話で話をしている人に"SonicExplorer"を向けると、私の耳元でささやいているかのように聞こえてくるのである。もちろん、遥か向こうといってもたかだか20mくらいではあるのだが、雑踏の先の20mというのはずいぶんと先に感じる。しかし、"SonicExplorer"の先のパラボラ面は見事にその遠く先の音を集めてくれる。
ところで、遠く離れた人の声はどうして聞き取れないのだろうか?それはもちろん、遠く離れた人の声は小さくしか聞こえなくなって、その人以外が発する雑音に埋もれてしまうからだろう。それでは、人がしゃべる声は距離が離れるとどの程度小さくなるだろうか?
音波が四方八方に等方に拡がっていくとすれば、音の大きさは音の発信源からの距離の二乗に反比例すると考えるのが自然である。つまり、喋っている人からの距離が10倍になれば、その人の声は1/100の大きさでしか聞こえないことになる。20m先で携帯電話で喋る人の声は、1m隣でささやく人の声のわずか1/400の大きさなのである。それでは、雑踏の中で溢れる他の音に埋もれてしまうのは当り前である。
そんな声を聞き取りたい時にはどうしたら良いだろう?そんな時、私達は耳に手を当てて、耳を澄ませる。掌で音を耳に集めて何とか声を聞き取ろうとするのである。それと同じく、この"SonicExplorer"は、先端のパラボラ面で焦点にあるマイクに音を集めて増幅するのである。それでは、"SonicExplorer"は私達の耳に比べてどの程度音を多く集めているだろうか?
そもそも、私の耳の大きさはどの程度だろう?耳はそんなに効率的に音を集めそうな形状をしているわけではなさそうだから、有効な集音面積としては直径1cmの円といったところだろう。それに対してこの"SonicExplorer"のパラボラは直径20cm程だ。ということは、直径にして20倍、面積にして二乗で400倍の面積で音を集めることができるわけである。音を集める程度は音を集める面積に比例するだろうから、"SonicExplorer"を使えば人間の耳の400倍もの鋭さで音を聞き取ることができるわけだ。400倍ということは、つまりは先ほどの「20m先で携帯電話で喋る人の声」と「1m隣でささやく人の声」との違いと同じというわけで、結局のところ"SonicExplorer"を使えば「20m先で携帯電話で喋る人の声」が「1m隣でささやく人の声」であるかのように聞き取ることができる、ということになる。
ここで面白いのは、音が小さくなってく様子は距離の二乗に比例し、音を集める量は集音面のパラボラの直径の同じく二乗に比例するから、n倍遠くの音を元と同じように聞き取りたかったら、集音面の大きさ(長さ)をn倍にしてやれば良い、という単純な関係にあることである。20m先の声を1m横の声と同じように聞き取りたかったら、耳の大きさ(長さ)を20倍にしてやれば良いのである。
そんなことを考えていると、ふと二十年位前のことを思い出した。その頃、私は夏になるといつも長野県の野辺山あるいは川上村というところに滞在していた。その数年前まで、私はその野辺山で暮らしていたのである。そして、野辺山にある45mミリ波望遠鏡の建設が佳境に入った頃だったのだろうか、その頃私の父は半分野辺山で暮らしていた。下の写真は八ヶ岳の麓にあるその45mミリ波望遠鏡である。
 http://www.icon.pref.nagano.jp/usr/minamimaki/sawayaka.htm |
そんな二十年位前のある日、父がこんなことを言った。
「45mのアンテナを赤岳(八ヶ岳の最高峰)に向けて、副鏡(焦点)の場所にいると赤岳の上にいる登山客達の話す声がまるで自分のすぐ横にいるかのようにガヤガヤと聞こえてくるんだよ」一体、それは本当だろうか?上の写真を見ても、赤岳(八ヶ岳の最高峰)の山頂は野辺山の45m望遠鏡の位置から遥か彼方に見える。少なくとも、その頃の私からすれば遥か先のずっと遠くに見えていた。今でもそれは同じことだろう。やっぱり遠く彼方に見えると思うし、その山頂でワイワイガヤガヤと話す登山客達の声が聞こえるとは思えない。
そこで、試しに地図で野辺山の45m望遠鏡と赤岳の山頂の距離を確かめてみると、直線距離にして10km程である。下の地図で赤い■の位置辺りが野辺山の45m望遠鏡が建っているところだ。10kmということは、メートルにして一万メートルである。メートルに直したところで、やっぱり遠いことには変わりない。
 |
それでは、先ほどの"Sonic Explorer"と同じように考えてみることにしよう。45m望遠鏡のパラボラ面は人間の耳(ここでも直径1cmとしよう)の45m/1cm= 4500cm / 1cm = 4500倍である。ということは、5000m先、すなわち5km先の音が1mのすぐそばにいる人の声と同じように聞こえるということになる。すると何ということだろう、10km先の八ヶ岳の山頂でワイワイガヤガヤと話す登山客達の声は、すぐ2m横でワイワイガヤガヤと話しているかのように聞こえることになる。もちろん、それは理想的な場合の話ではあるが、先の父の話は結局のところ何の不思議もないごく当り前の話だったわけである。
上の写真のような、八ヶ岳の麓にそびえる白い45m望遠鏡ももちろんかっこいいけれど、私が野辺山に住んでいた頃にはまだその45m望遠鏡は建っていなかった。私がいた頃には、下の写真の中に見える朱色の野辺山太陽電波観測所の野辺山干渉計のパラボラアンテナだけが野辺山の高原に点在していた。野辺山干渉計はもう今では現役ではないけれど、今でもやっぱりイースター島のモアイのように大空に向いているはずだ。私は白く輝く45m望遠鏡も大好きだけど、その横に点在している朱色に塗られた鉄骨で支えられている野辺山太陽電波観測所の野辺山干渉計の方が大好きだ。
 http://solar.nro.nao.ac.jp/nori/html/introduction-j.html |
現役を引退した今ではどうなのだか知らないけれど、野辺山太陽電波観測所の野辺山干渉計のパラボラアンテナは太陽電波を捕らえるためのアンテナだったので、いつも太陽の方を向いていた。まるで、巨大な向日葵のように忠実に正確に太陽のある方向にパラボラ面を向けていたのである。だから、太陽が強く照らす晴れた日も、薄暗い雨の日も朱色の鉄塔の上のパラボラアンテナを見れば、太陽の方角はいつも一目瞭然だったのである。
そういえば、私が子供の頃、一時間かけて歩く家から分校までの4キロメートルばかりの道端には、たくさんの月見草が咲いていた。高原の中で高くそびえる赤く巨大な「向日葵」達と、歩く私のすぐ横に咲いている黄色い「月見草」が私はとても大好きだった。
眩しい太陽を追いかける「向日葵」達も、静かに照らす月を見る「月見草」もどこか遠くの声を耳を澄ませて聞いているのだろうかとか、その声をすぐそば近くに感じているのだろうかとか、少し思ってみたりした。
2001-11-23[n年前へ]
2001-12-24[n年前へ]
■サンタが街にやってくる 
複数サンタクロースの巡回問題
簡易に書き直した2011年版もあります。
幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで(高原の診療所なのだから大して違いはないのだけれど)、とても不思議だった。
さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。
知らない人のために書いておくと、「巡回サンタクロース問題(TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが
- サンタクロース研究
- ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )
そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。
まず、始めに問題提起をしてみよう。
「果たしてサンタは一人なのか?」
どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。
そこで、まずはサンタの歴史から調べてみると、Santaさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。
とはいえ、Santaさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか?
また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
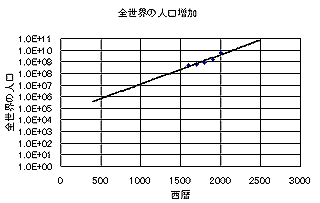 |
St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。
サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。
子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 |
どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。
先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。
そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。
それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
一例として、サンタが1,2,10人の場合を示してみる。
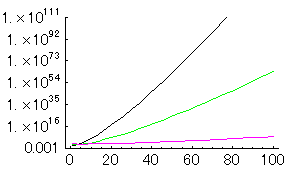 |
このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。
実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。
このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。
ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。
それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。
ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。
もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。
こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。
サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。

