2009-10-30[n年前へ]
■「京都市鴨川源流」を廻る「理系風デート」 
青春小説のようなシーンを交えながら、数学世界を解説していく「数学ガール
「じゃあー少しだけ、僕とデートしてくれませんか？」
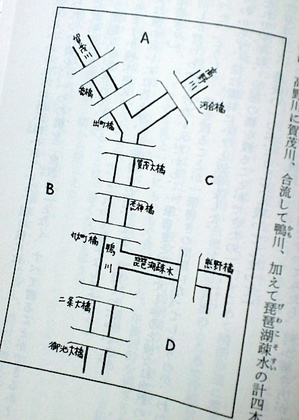鴨川の始まりである出町柳辺りから、御池大橋までを舞台に、オイラーが解いた「ケーニヒストベルグ橋の問題」を題材にして、ローマの休日風な素敵で切ない数時間（と数ヶ月）を描いた一話です。見事なくらいに、微妙な心の機微と数学の世界が一体化した素敵で少し切ない短編です。
午後四時になってもまだ陽の高い、京都の休日へ繰り出した。
実際には、「ケーニヒストベルグ橋の問題」を解くという口実の（体力的に疲れそうな）デートに、付合ってくれる女性は少なそうな気がします。・・・とはいえ、この「京都市鴨川源流」を廻る「理系風デート」の一話、「ローマ風の休日」はとても楽しめる話です。
「ローマ風の休日」は「ホルモー六景
ケーニヒスベルグの橋とは、プロシアの首都ケーニヒスベルグ（現在はロシア領カリーニングラード）を流れるプレーゲル河に架かる7つの橋のことである。この7つの橋を全て一度だけ渡り、元の場所に戻れるか、という議論によって有名となった。
ケーニヒスベルグの橋の問題は1736年に、数学者オイラーにより、地図を線と点で表現し、その図形を一筆書きできるかの問題と整理されて考えられた。その結果、一筆書きできない、すなわちケーニヒスベルグの7つの橋を求められた条件の下に渡る道順は無いとして、解決された。ケーニヒスベルグの橋は、グラフ理論とトポロジーの起源であると言われている。
ケーニヒスベルグの橋
さて、鴨川源流を舞台にした「ケーニヒスベルグの橋の問題」はどのような答えになるでしょうか。ノートの上で手と頭で解いてみても良いですし、京都の街を自転車で走り、この数学の問題を足と体で解いてみると面白いと思います。そんな「理系風デート」があると・・・さらに、楽しいでしょうね。
彼女ははそれから、いろいろな数学の話を聞かせてくれた。
2010-11-25[n年前へ]
■心斎橋で「数学パズル」デートをしてみよう!?
東京や大阪といった大都市を歩くとき、その足下に川が流れていることも多いものです。かつて地上を流れていた川の上が、今では道となり、その上を私たちが歩いていたりします。たとえば、大阪の心斎橋近くも、昔はいくつもの川が流れていたのに、今では、それらの川が流れていた場所には道路が建設されて、そして、その上を車が走っていたりします。
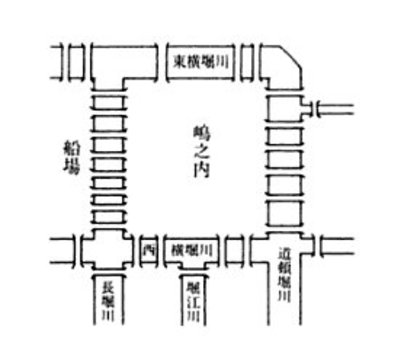いつか、そんな心斎橋近くに行く時、いつか「浪華二十八橋智慧渡」の町並みを実際に歩いてみたいと思っています。「浪華二十八橋智慧渡」というのは、江戸時代 水野忠邦が老中だった頃に出された和算書「算元算法」の中に書かれている数学の問題で、つまりは、日本版「ケーニヒスベルグの橋」問題です。心斎橋近くにかかる二十八の橋すべてを一筆書き状に渡ることができるか？という問題です。
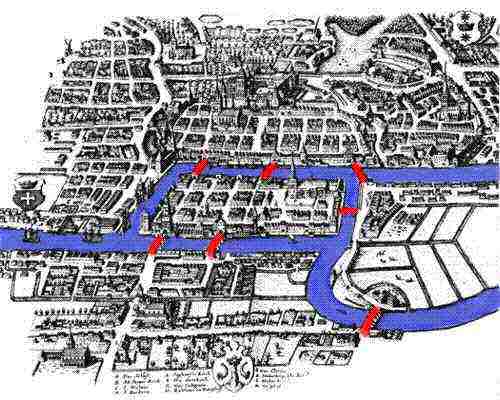「ケーニヒスベルグの橋」は数学者オイラーが解いてしまっているので、その変形でもある浪華二十八橋智慧渡は一目でその答え「一筆書きで通ることができるか」はすぐわかります。けれど、江戸時代の最先端の数学に描かれた町並みの上を自分の足で歩くことができると思うと、何だかゾクゾクしてきます。
大阪近くに住んでいて、時間だけはたくさんあるという人がいたら、心斎橋近くで「数学パズル」デートをしてみると面白いかもしれません。浪華の二十八の橋（があった場所）を、昔の景色を想像しながら歩き眺めてみるのです。そして、「一筆書きできない」ということを実感しつつ、一度歩いた場所を逆方向から歩いてみたりする・・・そんな、時間だけは贅沢に使う「数学パズル」デートはいかがでしょう？それは、とても得難い貴重な一日になるような気もします。
万城目学「ホルモー六景
大阪版「ケーニヒスベルグの橋」に限らず、あなたのいる街にそれぞれの「ケーニヒスベルグの橋」があることと思います。たとえば、京都なら右の絵のような「鴨川 DE ケーニヒスベルグの橋」といった具合です。そんな、ご当地「ケーニヒスベルグの橋」を見つけて、「数学パズル」デートをしてみるのはいかがでしょうか？
2011-02-06[n年前へ]
■街で見かけた「ケーニヒスベルクの橋渡り問題」
「街を流れる川に架かる7つの橋を、一筆書き状にすべて渡り、（どこでも良いから）スタート地点に戻ってくることができるか？」というのは、オイラーが解いた「ケーニヒスベルクの橋渡りの問題」です。ケーニヒスベルクというのは、今はカリーニングラードと呼ばれるバルト海沿いにあるロシアの街です。
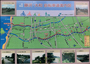
この「ケーニヒスベルクの橋渡りの問題」は、私たちの住む街にも、実はたくさんあったりするものです。たとえば、今日頂いた「街で見かけたケーニヒスベルクの橋渡り問題」が下の写真です。看板に描かれた川と、その川にかかる橋群は、まさに「ケーニヒスベルクの問題」です。「鉄道専用らしき橋を渡ることができるとしたら」とか「鉄道専用橋は渡ることができないとしたら」という風に、条件を変えながら眺めてみても面白そうな、そんな「ケーニヒスベルクの看板」に見えます。
あなたの街にも、きっと「ケーニヒスベルクの橋渡り問題」がどこかに隠れているはずです。今日頂いた「ケーニヒスベルクの問題」看板のように、あなたが見つけた、そんな風景（写真）「理系の散歩道」をお裾分けして頂けたら、心からうれしく思います。
2012-06-21[n年前へ]
■「ケーニヒスベルクの橋渡り問題」 藤沢・江の島"境川サイクリングロード" 編
天才オイラーが解き明かした「バルト海沿いにあるロシアの街ケーニヒスベルクで、街を流れる川に架かる7つの橋を、一筆書き状にすべて渡り、（どこでも良いから）スタート地点に戻ってくることができるか？」という”ケーニヒスベルクの橋渡りの問題”」は、私たちが日々過ごす街にも溢れています。
たとえば、神奈川県は川崎・鶴見の辺りにある『街で見かけた「ケーニヒスベルクの橋渡り問題」』や、あるいは京都の町で「鴨川源流で眺める理系風デート」…といったように、どんな町にも一筆書き問題は潜んでいるのです。
今日は、東京都町田市近くから神奈川の江の島に流れる「境川」に掲げられていた「ケーニヒスベルクの橋渡り問題」を眺め・挑戦してきました。これまでに挑戦した「橋渡り問題」の中では、最も橋が多く・距離も長い…巨大な「一筆書き・橋渡り問題」です。
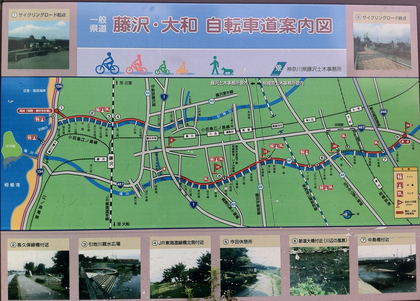
ところで、境川の「ケーニヒスベルクの橋渡り問題」は、江の島を領域に入れてしまうと、「一筆書きできないことは自明」です。何しろ、地図上は橋がひとつしか無いので、江の島は「その場所をスタート地点としたら、戻って来ることができない、けれど、通過することもできない場所」であることが明らかだからです（本当は、江の島には橋が２本かかっているのですけどね）。
…かつてケーニヒスベルクと呼ばれたバルト海沿いのカリーニングラードという街に、「江の島」のような島があったとしたら、オイラーのような天才でなくとも、容易に「ケーニヒスベルクの橋渡り問題」を解き明かすことができたのかもしれない、一筆書き問題が成立するための条件をいともたやすく気づいたのかもしれない、と想像したりします。
これが、今日眺めた「理系の散歩道」です。
2012-10-23[n年前へ]
■巡回セールスマン問題の答が描く「一筆書きアート」
一年ほど前、「数百個の数字をエンピツで結んでいくアニメーション」を作ってみました（”点と点を結んで行くと浮かびあがる”スティーブ・ジョブス）。
この"Connecting the dots"な一筆書きラクガキ…「散らばっているたくさんの点たちを結んでいく絵」は、ペン先が何回も・何度も同じような場所を往復しています。つまり、右往左往が繰り返される、あまり効率的でない「描き方」です。
もしも、たくさんの点が散らばっている時、それらの点を「一番効率的に」「最も最短で描く」にはどうしたら良いでしょう？…ということを考え始めると、それは「巡回セールスマン問題」という問題に変わります。
巡回セールスマン問題（じゅんかいセールスマンもんだい、Traveling Salesman Problem、TSP）は、都市の集合と各2都市間の移動コスト（たとえば距離）が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路の総移動コストが最小のものを求める（セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める）組合せ最適化問題である。
巡回セールスマン問題
"TSP ART"（＝巡回セールスマン問題的アート）と画像検索すると、数多くの街を廻るセールスマンのように、たくさんの点群を結ぶという作業を、最も効率的に行った「たくさんの一筆書き」アートを見ることができます。画像の「濃い部分」に「”たくさんの点”」がばらまかれているようにした上で、それらの点を最も効率的に結んでいくのがTSP Artです（参考：TSP Art）。
この巡回セールスマン問題的アート（TSP Art）を描くのは結構大変です。何しろ、たとえば16階調で256×256の絵を描こうとすると、16×256×256…つまり1万048千576の点を「辺り一帯」にばらまいて、その1万048千576もの点を最も効率的に移動するにはどうしたら良いか？という超大規模な巡回セールスマン問題を解かなければならないからです。
しかし、巡回セールスマン問題的「一筆書きアート」は大変でありつつ、とても素朴で魅力的です。こんなラクガキ、何だか少し描いてみたくなりませんか？
」など。