2000-04-07[n年前へ]
■Canon Simplex + 
オリジナルとコピーの追復曲
野田秀樹、NODA MAPの新作「カノン」が上演されている。観に行きたいのだが、距離のせいかなかなか見に行けそうにない。
観ていないので内容は知らないのだが、タイトルのカノンは「規範」を意味するギリシャ語のkanonだろう。英語で言えばcanonである。辞書でカノン(canon)を調べてみると、
- 規範、原則、標準、規準、根本原理 類似語 = "criterion"
- 基本的重要文献
- 真作品
- 教会法
- 聖書正典、正経
- 音楽形式のカノン、追復曲
- 48ポイントの活字
ちなみに、音楽形式としてのカノン=追複曲は、「主題としての一声部が応答としての他声部に模倣される形式」とある。「かえるの歌が聞こえてくるよ…」はその単純な例である。一つのメロディから導き出された旋律が重なり合っていくわけだ。あるいは、山下達郎の「クリスマスイヴ」の中間部のパッヘルベルのカノンといった方がわかりやすいだろうか。
音楽形式の「カノン」では、最初の旋律が主題であり原典である。そして、その模倣旋律が組合わさって、魅力的な音楽が作られていく。
ところで、「カノン」という言葉の意味の大きな割合を占める「聖書」という言葉を考えた時、音楽形式である「カノン」と似たようなものがある。
それは印刷技術である。と、書くと、唐突に感じるかもしれない。しかし、聖書の複製をきっかけとして広まった技術が、印刷技術である。それほど、関係がないわけではない。印刷技術は、グーテンベルク(ちなみに、今年はグーテンベルク= Gutenberg, Johann Gensfleischの生誕600年目である)の「42行聖書」から始った原典を複製する技術である。
印刷技術は、一つの原典から複数の複製物が作り出されていく。それは、一つの旋律から導き出された複数の旋律が追いかけていく、音楽のカノンそのものである。印刷技術はもうひとつの「カノン」なのである。
 |
本来、「カノン」という言葉は「規準、原典、教典」を指すわけであるが、同時に、この「カノン」という言葉には「複製」という匂いがつきまとう。先の追復曲=カノン、そして印刷された聖書もそうだ。
グーテンベルクの「42行聖書」は200部程度印刷された。それらはいずれも色々な装飾がされ、同じ物は一つとしてない。どれも個性豊かなものである。音楽の「追復曲=カノン」でも、輪唱のようなごく単純なカノンを除けば、旋律は魅力的に変化されていく。旋律はどれも個性豊かなものである。個性がなければ、それはとてもつまらない輪唱に終わってしまう。
きっと、NODA MAPの「カノン」では野田秀樹の「言葉を繰り返し、次々と意味を転じさせて、そして、何者かを描写していく力」が発揮されるのだろう。考えてみれば、野田秀樹の「言葉を操るやり方」もカノンそのものである。模倣から始まったモノであっても、何かが新たに加えられていくならば、それは模倣でなくなって、きっといつかは原典になるのだと思う。逆に、あまりに原点としての「カノン」を守ろうとしたものは、それは単なる「コピー」に終わる。
さて、ところで「コピー」という言葉と「canon」という言葉を考えるとき、ある企業(が頭の中に浮かぶ。「Xerox」というオリジナル旋律に派生する企業である。
原典とされた「Xerox(富士ゼロックス)」はかつて、丸善石油のCM「オー・モーレツ!」を原典として、「モーレツからビューティフルへ」というCMを作り上げた。それは素晴らしい本歌取りである。60年代を代表する「オー・モーレツ!」という「キャッチ・コピー」を、「コピー」して、さらに変化させることで70年代へ繋がる「モーレツからビューティフルへ」という「キャッチ・コピー」を作り上げたのである。それはもう、一つの哲学であるといって良いと思う。
一方の企業は80年代に苺の「コピー」にミルクをかけてみせ、「本物と"コピー"の違いは見分けられない」というCMを作り上げた。原典と「コピー」に違いがあるのか?という問いかけである。それもまた一つの哲学だろう。
原典にこだわりすぎ、単なる「コピー」に終わるか、それとも、何者かを加え「本歌取り」としての「カノン」にすることができるか、それは「Vision」の有無にかかっている、のかもしれない。本当の「カノン」になるかは、「Vision」次第だ。そんなに深い意図はないし、適当に書いてみただけだけれど。
うーん、今回はやっぱり、「スクラップ」行きだな。(BGM & Title ゴルトベルグ変奏曲による14のカノンJ.S.Bach)
2001-09-24[n年前へ]
2001-12-24[n年前へ]
■サンタが街にやってくる 
複数サンタクロースの巡回問題
簡易に書き直した2011年版もあります。
幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで(高原の診療所なのだから大して違いはないのだけれど)、とても不思議だった。
さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。
知らない人のために書いておくと、「巡回サンタクロース問題(TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが
- サンタクロース研究
- ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )
そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。
まず、始めに問題提起をしてみよう。
「果たしてサンタは一人なのか?」
どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。
そこで、まずはサンタの歴史から調べてみると、Santaさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。
とはいえ、Santaさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか?
また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
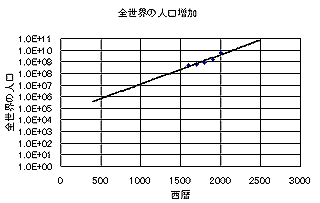 |
St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。
サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。
子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 |
どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。
先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。
そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。
それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
一例として、サンタが1,2,10人の場合を示してみる。
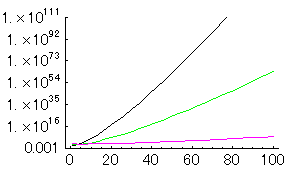 |
このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。
実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。
このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。
ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。
それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。
ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。
もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。
こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。
サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。
2005-01-14[n年前へ]
■両手を広げた小さなキリスト像 
阪神大震災の時に有名になったカトリック鷹取教会の両手を広げた小さなキリスト像のいくつかの話
「何が奇跡だ。あんなのは、ただのデク人形だ」「奇跡(なんていう言葉)よりも、(キリスト像の足下には)ずっと中身の濃いものが詰まってるんだ」(両手を広げた小さなキリスト像の)台座にはタイムカプセルが埋まっている。中身は(ボ−ト・ピ−プルだった)信者の子供が書いた作文や、(信者たちの)ボ−ト・ピ−プル当時の写真だ。
2008-01-05[n年前へ]
■「宗教革命」と「フェルメール」 
 フェルメールはピーテル・ブリューゲルの100年後、新教が主流となったネーデルランド、それ以前のような宗教画を書くことはできない(もしも書いたとしたら「偶像崇拝である」と新教教会から弾劾される)時と場所に生きた。つまり、教会からの宗教画の注文が消え画家たちが路頭に迷い、豊かな市民たちへ肖像画・風景画を描くことを生活の糧にする、そんな時代を生きてた。だから、かどうかは知らないが、フェルメールの描く油絵には、まるでケータイ写真で撮影したような、普通の日常生活が写っている。
フェルメールはピーテル・ブリューゲルの100年後、新教が主流となったネーデルランド、それ以前のような宗教画を書くことはできない(もしも書いたとしたら「偶像崇拝である」と新教教会から弾劾される)時と場所に生きた。つまり、教会からの宗教画の注文が消え画家たちが路頭に迷い、豊かな市民たちへ肖像画・風景画を描くことを生活の糧にする、そんな時代を生きてた。だから、かどうかは知らないが、フェルメールの描く油絵には、まるでケータイ写真で撮影したような、普通の日常生活が写っている。
この瞬間にケータイを手に持って何かを眺めている人は一体どういう景色を、どんな風に見ているのだろうか。
