hirax.net::Keywords::「方程式」のブログ

■あみだくじ方程式を1次元拡散方程式を使ってエクセルで解いてみる　

　あみだくじを作ったとき、「アタリ」がどのような分布になるかは、大雑把には、拡散方程式で解くことができます。もし、あみだくじに横線があれば、右へ行ったり・左に行ったり、酔った人がさまよい歩く酔歩（ランダムウォーク）のように「アタリ」を選ぶことができる場所が、推移するわけです。

　たとえば、拡散方程式を横軸を縦線感覚で離散化し、縦軸は…これまた適当に離散化し、縦方向単位長さ移動するときに、どれだけ左右への移動が生じるか（＝横線が縦線に対して、どの程度の頻度で存在するか）を考えてやり、そしてその離散化された拡散方程式を解いてやれば「あみだくじ」のアタリ分布を計算することができます。

　左端と右端の「境界条件」では、そこで「折り返されたような」動きをするわけですから、ノイマン条件を適用してやればよいことになります。また、時間ステップは、いつものように「循環参照による手動再計算」を用いて実現してやれば良い、ということになります。

　というわけで、エクセルでプロトタイピングして、作ってみたのが下の計算シートです（作成したエクセルシートはここに置いておきます）。たとえば、下のグラフは、アタリが左から３番目縦下部にあった場合に、一体、どの縦線を選ぶの良いかを示す確率分布になっています。今のこの状態なら、左から１番目、２番目、３番目が大体同じアタリ確率になっていて、もう少し細かく眺めてみると、左から２番目を選ぶのが一番アタリをひく可能性が高い、ということがわかります。

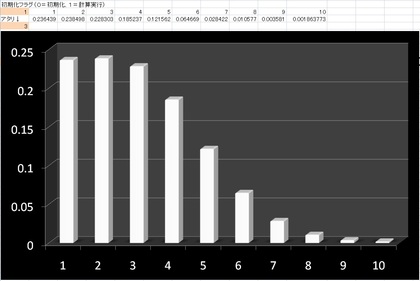
　上の例の場合には、一番アタリをひく可能性が高い線が、アタリのある真上より少し端側に寄りました。この「アタリをひく確率が高い線が端に寄る」傾向は、横線が多いほど激しくなります。…とはいえ、あみだくじを作る時のことを考えると、実際にはあまり横線の数が多くないように、つまり、手抜きあみだくじが多いように思います。

　そんな時は、手抜きあみだくじをするときは、アタリの真上近くを選び、そうでない場合にはアタリに近い端っこを選ぶ、というのが、あみだくじ方程式から導き出されるおトク知識と言えるのかもしれませんね。

■顔文字で記した「拡散方程式」　

　「式」を眺めると、その中に「顔」が隠れ見えることがよくあります。たとえば、正規表現の中にはたくさんの顔たちが整列しているものです。

　これが今日の正規表現の心象風景です。「本を真面目に読んでみたけれど、よくわからず頭の中にハテナマークが浮かび上がり、いつの間にかこめかみで血管がピクピクしていて、ついにちゃぶ台をひっくり返していた…」という感じです。

　式の中に「顔」が隠れているというのは、正規表現の「式」に限りません。方程「式」の中にもたくさんの顔が隠れています。

　たとえば、「何かが（時間的に）刻々と広がってく量は、その何かの空間的な傾きで決まる」という拡散方程式を、物理量をφ(r,t)と記し・さらにナブラ演算子を使って記述した拡散方程式などを見ると、私には「左利きの人が筆記用具を手にして、耳をかきながら、うつむき気味に何かを考えている」「その横には横を見ながら、口を尖らせている」ようすに見えてしまうのです。そんな「顔文字で記した拡散方程式」が下の板書です。

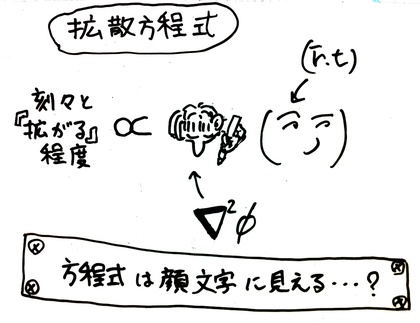
　「よくわからないもの」が顔に見えてしまう、ということはよくあるものです。壁の染みや、記念写真の後ろの木々、…はたまた月面のクレータまで、人は人の顔を「よくわからないもの」の中に見いだします。

　正規表現や各種方程式が「よくわからないもの」というのが、実に悲しい技術オンチぶりですが、そんな人はきっと私だけではないだろう、と信じたいところです。あなたは、どんな顔文字を数式やプログラムコードの中に見ることがありますか？

■Mathematica版「おっぱい（曲面）方程式」で「あなた好みのおっぱい」を作る!?　

　「Wolfram CDF PlayerをMathematicaとして使う方法」をRubyでもっと簡単にしてみたので、次は数式処理のみならず汎用処理が可能なプログラム言語であるMathematicaで、何かの処理をさせてみたくなります。まず手始めに、何かをしてみようとなると「オッパイ的なHelloWorld」を作ってみたくなります。

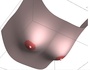
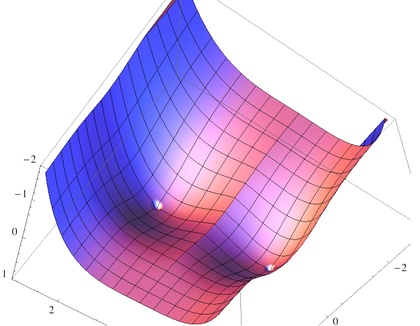
　タイムリーなことに「おっぱい（曲面）方程式を作り出した」という世紀の大発見がありました。そこで、まずはハロー・オッパイということで、Mathematica版「おっぱい（曲面）方程式」を書き、「Wolfram CDF PlayerをMathematicaとして使う方法」をRubyでもっと簡単にしてみたのやり方を使い、Universal Mathematica Manipulator 3でおっぱい（曲面）方程式を描いてみました。描いた結果が右上画像です。

　さて、最初のプログラム（HelloWorld）を書いたなら、次はちょっとカスタマイズして「プログラミングの楽しさを知る」というのが、学びの王道です。そこで、少しだけMathematicaの機能を使ってカスタマイズしてみた結果が下のようすです。「おっぱい肌色方程式」を曲面を塗りつぶす色に対して適用させることで、もっと写実的!?にビジュアリゼーション（可視化）してみました。

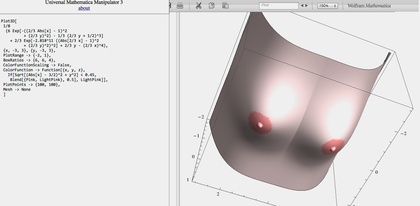
　「オレもやりたい」と思ったならば、やることはとても簡単です。「Wolfram CDF PlayerをMathematicaとして使う方法」をRubyでもっと簡単にしてみたのやり方（もしくは「Wolfram CDF PlayerをMathematicaとして使う方法」のやり方）でWolfram CDF PlayerをMathematicaとして使うことができるようにして、後は下記のコードを貼り付け・演算ボタンを押すだけ、です。もちろん、「Mathematicaを持っている」という人であれば「下記のコードをコピペするだけ」で終わりです。それだけの作業で、グリグリとおっぱいを後ろから前から眺めることができます。

Plot3D[
1/8 
  (6 Exp[-((2/3 Abs[x] - 1)^2
    + (2/3 y)^2) - 1/3 (2/3 y + 1/2)^3]
    + 2/3 Exp[-2.818^11 ((Abs[2/3 x] - 1)^2
    + (2/3 y)^2)^2] + 2/3 y - (2/3 x)^4),
 {x, -3, 3}, {y, -3, 3},
 PlotRange -> {-2, 1},
 BoxRatios -> {6, 6, 4},
 PlotPoints -> {100, 100},
ColorFunctionScaling -> False,
 ColorFunction -> Function[{x, y, z},
   If[Sqrt[(Abs[x] - 3/2)^2 + y^2] < 0.45,
    Blend[{Pink,LightPink},0.5],LightPink]],
 Mesh -> None
 ]

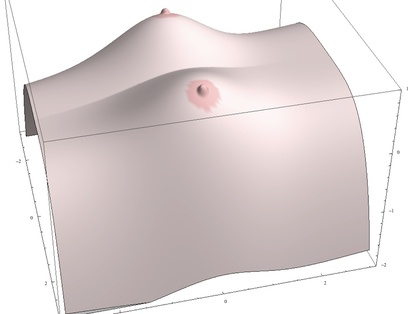　"If[Sqrt[ (Abs[x] - 3/2)^2 + y^2 ] < 0.45, Blend[ {Pink, LightPink}, 0.5], LightPink]],"辺りの記述には、各自それぞれ意見があることでしょう。たとえば"0.45"という部分、あるいはBlend[ {Pink, LightPink}, 0.5]の比率（色）に関する部分…そうしたパラメータ（関数）をほんの少し変えただけで、驚くほど印象が変わるものです。たとえば、"0.45"を"0.35"に、"0.5"を"0.7"に変えてみたのが、右の「おっぱい曲線方程式」です。これだけでも、ずいぶんとニュアンスが変わって見えるものです。0.3でも0.4でもなく、0.45（とか0.35）にするといった小数点以下さらに数桁にこだわるのが「匠（たくみ）のワザ」なのです。…こうしたカスタマイズを繰り返すことで「あなた好みのおっぱい（曲面）方程式」を作り出してみるのも興味深いのではないでしょうか。

　というわけで、ハロー・グッバイならぬ、ハロー・おっぱい…じゃなかった（「Wolfram CDF PlayerをMathematicaとして使う方法」を利用した）Mathematica版ハロー・ワールドを今日は学んでみました。 それにしても、おっぱいの世界は実に奥が深いものですねぇ。

---

　この続編が、下記の「エクセルで「バスト（曲面）方程式」を描いてみよう!?」です。

　Mathematica（もしくはCDF Player活用）は敷居が高いだろうから、エクセル版も作ってみました。というわけで、エクセルで「バスト（曲面）方程式」を描いてみよう!?　（シート付）です。

エクセルで「バスト（曲面）方程式」を描いてみよう!?

---

＊各種環境へのポーティング（移植）例：

1. Mac OSX Grapher版
2. Wolfram Mathematica版
3. Microsoft Excel例
4. Maxima版
5. R 版

■エクセルで「バスト（曲面）方程式」を描いてみよう!?　

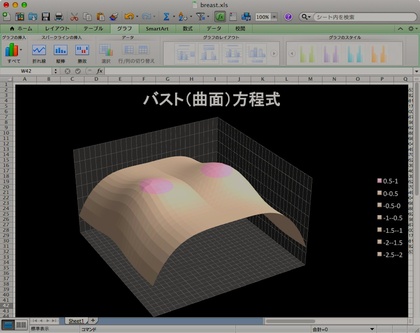　今日は、世紀の大発見「バスト（曲面）方程式」をExcelで描いてみようと思います。昨日は、Mathematicaでカラフルにカスタマイズしたバージョンを描いてみましたが、Mathematicaではやはり敷居が高いのではないでしょうか。Mathematicaをすでに持っている・インストールしている人であればともかく、そうでない人は「CDF PlayerをMathematicaっぽく使うために、まずはCDF Player をダウンロードする」という作業をしなければならないことも多いだろう、と思います。…それは少し面倒です。そこで、「いいおっぱいの日＝１１月０８日を前にした今日、"xls"フォーマットの「バスト（曲面）方程式」シートを作ってみました。

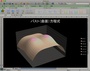
　右上の画像が、Excel 2010で描いた「バスト（曲面）方程式」です。もちろん、このバージョンもカラーフルにカスタマイズされたバージョンです。この実に立体的・魅力的な曲面を描き出すエクセルのシートはこちらに置いておきます（breastEquation.xls）。もしも、カラーマッピングを変えたいと思う場合には、

1. 凡例の分割数を変える
2. 値が大きな部分の凡例を”適度な”数だけ色を設定する

という手順で、任意の!?カスタマイズが可能です。

　Wolfram Mathematica版、Microsoft Excel 版、VBA版、R版、C# with .NET版…ありとあらゆる道具を使って、深遠で魅惑的なバスト（曲面）方程式の姿が、これから描き出されていくのではないでしょうか。そして、方程式の姿を決めるパラメータ群に潜む秘密も明らかにされていくに違いないのです。

　「おっぱい（曲面）方程式」の形状と色を、カスタマイズしてみた人がいたならば、一体どういう風にカスタマイズしたかを、ぜひ知りたい今日この頃だ。これは、意外なほどに深層心理が見え隠れして、「本当は怖い心理テスト」であったりするのかもしれない。

「本当は怖い”バスト（曲面）方程式”のカスタマイズ」

■「高校・大学の頃の自分」に送る「短く具体的なメッセージ」　

　Shiroさんの「知的なツール、努力の方法」から、"I'm not as smart as I thought I was. "（日本語訳：僕は自分が思っていたほどは頭がよくなかった）を読んだ。

　悩む高校生に対して返されたMIT卒業生によるアドバイスを、高校生だった頃の自分が読んだとしたら、間違いなく「どうすればいいのか、全然わかんないよ…」と思うだろう。 「…意味分からないし。もっと、短くて・具体的に何を・どうやればいいか教えてくれよ」と感じるに違いない。 あるいは、「高校の卒業生総代に選ばれなかった」とか「MITに行けなさそうだ」という（天上界の）高校生の悩みに対して、「頭のいいヤツはこれだからよー」と斜に構えたコトを考えるだけかもしれない。

　「MIT卒業生によるアドバイス」は昔の自分には絶対に届かない。 だから、高校生だった頃の、そして大学生になった頃の（他の誰でもない）自分自身に向けて、短く・具体的なメッセージを書いてみることにした。 そのメッセージは、たった２つだけだ。

　１番目のメッセージは、世界（つまり、自分の先にある未来）は「わからない」ものがたくさんある、ということだ。 だから、「ぼくの頭ではわからない…」と感じ、自信を失い・不安になるような状況は、もう数え切れないくらい何度も何度も繰り返し訪れ続ける、ということだ。 それまでに獲得した「（特定の）力・道具」だけでは、乗り切れそうにないように思えるかもしれない時が、それはもう何度も訪れる。 …そんな状況や不安と折り合いをつけ・それに負けずに共存していくために必要な「方法・能力」について書いたのが、次のメッセージだ。

　２番目のメッセージ、それは「好奇心・興味」を持ち、「未来・可能性・したいこと」を想像し・見つけ出す心を持て、ということだ。 それが、どんなにくだらなく思えることでも、何か「自分が楽しくなる・それをやりたくなる・そこまで辿り着きたくなる」ものを夢見て・焦がれる心を大切にしろ、ということだ。 「好奇心・興味」や「未来・可能性・したいことを想像し・見つけ出す気持ち」が大切でとても有効だということを、その証明を次に書く。

　「手に入れる結果」というものは、どうやら「努力した量」と（やはり）「天性の力」が掛け合わされたものと一致するようだ。 それは、つまりこんな方程式だ。

手に入る結果 ＝ 天性の力 × 努力した量

多少の誤差はあるようだが、この方程式は結構正確だ。 「手に入れる結果」に「天性の力」は関係ないと言ってしまえば、多分それはウソだ。 きっと、それは間違っている。 「手に入れる結果」は「努力した量」でも決まるが、「天性の力」にも比例する。 同じ時間努力しても「手に入る結果」は人それぞれ違う。 そこには確かに「天性の力」が関係している。

　「天性の力」を意志で変えることができないのであれば、その分「努力する量」を増やせばいいという言い分は多分真実に近いのだろうと思う。 …しかし、「努力する量」をただ増やせばいいなんていうメッセージを他ならぬ君に送るつもりは全くない。 それでは、ただの精神論で、その精神論を実践する根性も忍耐力も、残念ながら君は天性持ち合わせていないということを、（君と同じ本人である）私が一番よく知っているからだ。

　重要なヒントは、上に書いた方程式だ。 この方程式は、「右辺が左辺を決める」と読めるかもしれないが、それと同時に「左辺が右辺を決める」とも読むことができる。

努力する量 = 手に入る(だろう)結果 ／ 天性の力

この方程式に登場する「定数」は、実は「天性の力」だけだ。 「手に入れる（だろう）結果」と「努力した（する）量」は、それは間違いなく「変数」だ。 「努力した量」で「手に入れる結果」が決まるとも言えるが、それとは逆に、「手に入れる（だろう）結果」次第で「努力する（できる）量」が決まる、とも言える。 つまり、「手に入れる（だろう）結果」を、豊かな想像力・妄想力で描いて・それを欲すれば、「努力する量」はいくらでも増える、ということだ。

　「天性の力」を増やすことができなくても、「手に入れる結果」…その楽しさ・面白さを想像し拡大することは、無限にできるはずだ。 タダなのに無限に使うことができるという存在、それが想像力だ。

　努力した量が手に入る未来を決めるんじゃない、無限の好奇心・興味・未来や可能性を想像して見つけ出す心・自分が楽しくなる何かを見つけ辿り着きたいと欲する心…それが、「無意識のうちに努力する量」を限りなく増やし、そして未来を作り出していくんだ。 だから、世界を見て・未来を想像して・くだらない好奇心やささいな興味を大切に持ち続けて欲しい。 それらは、不確実で・わからないことばかりで・変化し続ける世界の中でも、いつだって、その先へゆっくりと歩き続けようとする「原動力」になるはずだ。

　さて、こんなメッセージを（年の離れた）君に送った理由は、もうバレているに違いない。 つまりは、２１世紀ののび太（の子孫）が２０世紀にドラえもんを送った理由と同じようなものだ。 21世紀を歩く未来の僕を作り出すだろう20世紀にいる君が、「夢を見て・何かを手に入れたいと思う欲望・気持ち」を少しでも増やしてくれるといいなと…君の未来は他（？）力本願に願っているわけだ。

　未来を作る「原動力」は、未来に対する無限の欲望や想像力だ。 未来を夢見て、自由自在に描き出し、そこへ辿り着きたいと願う力を、大事に抱えて続けて欲しい。