hirax.net::Keywords::「Scheme」のブログ

■「もしあなたが部屋の中で一番賢い人だとしたら」　

　「Squeaker大島芳樹のカリフォルニア日記」の「アラン・ケイ UCLAの授業」及び「ポジティブ・フィードバック」を読み、アラン・ケイ(Alan Kay)が引用したJames Watsonの言葉を知る。

If you are the smartest person in the room, you are in the wrong room.「もしあなたが部屋の中で一番賢い人だとしたら、　あなたは間違った部屋にいる」

If you are the smartest person in the room, you are in trouble. Because, nobody can help you.

■自分が目指す価値基準　

　下に引用した部分より、むしろ『自分(達)のやっていることが学校の中だけの価値基準で判断されることに強く反発していたのは覚えている。「しょせん高校の部活動、 3年間楽しんで、卒業したら懐かしい想い出」、そういうのがすごく嫌だった。未熟ではあっても、それが「大人」が本気でやるような「本物の仕事」に連続的に接続しているものであって欲しかった』という部分を眺めた『「ハッカーと画家」を訳していて、唯一ピンと来なかった章が "Why nerds are unpopular" だった』

それこそがNerdの特質なのではないか。特定集団内の相対的人気度ではなく、外にある問題を自分がどれだけ解けるかという絶対的な尺度にこそ価値を見出す、っていう

■「"複雑極まりない"複素平面」上に「仕事」と「趣味」を描く　

　複素平面"complex plane"は、複素数"complex number"の実部をx軸(実軸=real axis)・虚部をy軸(虚軸 = imaginary axis)にプロットしたものである。3+2iという複素数であればxy平面にx=3,y=2にを示す、そんな平面が複素平面だ（iは虚数単位=2乗した時に-1になる数である）。

　『「仕事」と「趣味」を2次元マップで1分以内に描け』言われたら、あなたならどう描くだろう？(同世代の)"Schemeを愛するプログラマ"が描いた「趣味と仕事の関係を描いた2次元チャート」を眺め、ふと私も「仕事」と「趣味」のイメージを2次元マップに描いてみたくなった。

　趣味を訊かれるといつもちょっと困る。私には趣味と仕事の違いがよくわからないからだ。
　　　Shiro Kawai

　人によって「仕事」と「趣味」というものの捉え方は違うだろうけれども、できる限り一般的に「仕事」と「趣味」という領域を2つの軸上に配置させるとしたら、どのように「仕事」と「趣味」を描くだろう？そんなことを「クイズの回答者になった気分で」描いてみたら、それは「複素平面」だった。(その人自身に対する)実利的・物質的でまさにリアルな"Real axis"と、イメージ的な「心の軸」を示す"Imaginary axis"というまさに実軸・虚軸で表現された複素平面である。

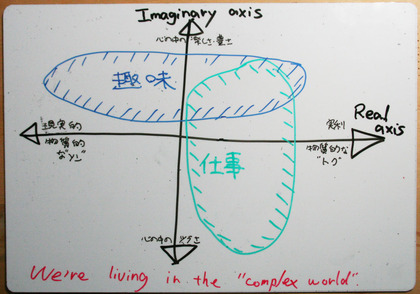
　この複素平面の縦軸(の上方向)は、自分の心を豊かにする軸と捉えることができるだろう。「虚」という文字よりは、"Imaginary"という文字で捉えたい「(その人自身の)心の満足」を示す軸、である。
　そして、横軸（の右方向）は、その人自身を実利的に満足させる軸である。しかし、その自分への「実利」という軸は、実は他人が何らかの形で価値を感じたことを示す軸でもあると思う。なぜなら、その「実利」は「他者が得た価値」が回りまわって流れてきたものに違いないからである。他人が得た満足が姿を変えたものであるから、である。つまり、この複素平面の横軸は「自分への実利」を示す軸であると同時に「他者を豊かにする軸」なのである。

　ひとことでまとめてしまえば、この複素平面は「本人(自分)の満足」と「他人の満足」という２つの軸で形作られる平面なのだ。

'Cause we are living in a material world. You know that we are living in a material world.
　　Madonna "Material Girl"

　その人ごとに「仕事」と「趣味」の位置づけがあると思う。どんな軸を使って、どんな風に「仕事」と「趣味」を捉えるかは、みなそれぞれ違うはずだ、と思う。「自分の中で辛さを感じながら、実利を得る仕事」もあれば（右下の象限）、「自分自身の楽しさとともに実利を得る仕事」もあるはずだ（右上の象限）。そして、さらに言うならば、同じ仕事であったとしても、その仕事がどこに位置するかは、人それぞれ異なっているだろう、と思う。そして、同じ一人の人がする同じ仕事であったとしても、きっと「その捉え方」「その座標」は変化し・移動していくものだろう、と信じている。

俳諧で「虚実」ということがしばしば論ぜられる。数学で、実数と虚数とをXとYとの軸にとって二次元の量の世界を組み立てる。虚数だけでも、実数だけでも、現わされるものはただ「線」の世界である。二つを結ぶ事によって、始めて無限な「面」の世界が広がる。
　　　寺田寅彦　「無題六十四」

　もしも、上に描いた複素平面="Complex plane"、それを言い換えれば言葉通りの「複雑極まりない世界」の上に、今のあなたが抱えているだろう「仕事」と、あなたが楽しんでいるかもしれない「趣味」は、どんなXY座標上にプロットされるだろうか。"複雑極まりない"複素平面上に、あなたはどんな軌跡を描いているだろうか。

■アンディ・ウォーホルと"work"　

　「コピーの時代」という企画展示を以前見に行った。

　四条河原町を歩いていると、古本屋のドアに貼られた「コピーの時代」と書かれたそのチラシにふと目を惹かれた。あまりに気に入ったので、琵琶湖近くにある滋賀県立近代美術館に行ってみた。

　その企画展の中には、もちろんアンディ・ウォーホルもいた。そんな、アンディ・ウォーホルの言葉を眺めていると、心に引っかかる言葉が多い。たとえば、そんなものの一つがこれだ。ポール・グレアムの「知っておきたかったこと」を読み、「好奇心を持っていると、努力が遊びになる」という一節に頷(うなづ)いた人は、きっとこんな言葉に頷(うなづ)くことだろう。

Work is play
when it's something you like.

I'd like to work in Europe.
But I wolud'nt do the same things,
I'd do different things.

　そんな疑問への答えは、「コピーの時代」のアンディ・ウォーホルは、どのように用意していたのだろうか。

...Making money is art
and working is art
and good business is the best art.

■Mathematica、Scheme（MIT Scheme）、Lispによる不完全性定理についての「ゲーデルの証明」　

　Mathematica、Scheme（MIT Scheme）、Lispで ゲーデルの定理：「この命題は証明できない」（真なのに証明できない命題がある）を書いた、「不完全性定理についてのゲーデルの証明」