2008-06-09[n年前へ]
■Photoshopプラグイン開発環境(PDLS)再び 
 Photoshopプラグイン開発環境 Photoshop DLL Linking System (PDLS) のページを(旧Pukiwiki)のファイルを元に書き直しました。PDFの説明ファイルの2004/08/07版はこちらになります。また、サンプルソース・バイナリファイルはこちらです。
Photoshopプラグイン開発環境 Photoshop DLL Linking System (PDLS) のページを(旧Pukiwiki)のファイルを元に書き直しました。PDFの説明ファイルの2004/08/07版はこちらになります。また、サンプルソース・バイナリファイルはこちらです。
 AmetMultiのモットーは「ATOKから何でもできる」でしたが、PDLSのモットーは「Photoshopから(その人のレベルに応じて)何でもできる」でした。(Photoshopの規約は気にせず)Cを使ってネイティブ・プラグインを気軽に書くこともできれば、GUIを使った連続作業などで自動的にマクロ関数(プラグイン)をお手軽に作ることもできる。その人のレベルに応じて、ステップアップすることができるPhotoshopのプラグイン開発環境というわけです。
AmetMultiのモットーは「ATOKから何でもできる」でしたが、PDLSのモットーは「Photoshopから(その人のレベルに応じて)何でもできる」でした。(Photoshopの規約は気にせず)Cを使ってネイティブ・プラグインを気軽に書くこともできれば、GUIを使った連続作業などで自動的にマクロ関数(プラグイン)をお手軽に作ることもできる。その人のレベルに応じて、ステップアップすることができるPhotoshopのプラグイン開発環境というわけです。
 マクロ関数やネイティブ・プラグインを組み合わせれば、さらにカスタムプラグインを作ることもできます。また変数を使ったり演算や数式処理も使えて、NEWやDELETEといったマクロを使い、局所領域に対してだけ演算を行うこともできます。そして、マクロプラグインには自動的にGUIをかぶせることもできるのです(GUIコードを書かなくても、ダイアログで変数設定などを実行時にすることができる)。
マクロ関数やネイティブ・プラグインを組み合わせれば、さらにカスタムプラグインを作ることもできます。また変数を使ったり演算や数式処理も使えて、NEWやDELETEといったマクロを使い、局所領域に対してだけ演算を行うこともできます。そして、マクロプラグインには自動的にGUIをかぶせることもできるのです(GUIコードを書かなくても、ダイアログで変数設定などを実行時にすることができる)。
 また、表計算アプリとの連携や鳥瞰図表示のプラグインもついている……というテキトーな機能てんこ盛り、の環境です。Photoshop Elementなんかで使うこともできますので、画像処理で遊んでみたい人は一度使ってみても良いかもしれません。いつものように、SYSTEMコールもできるプラグインなので、つまりは何でもし放題のプラグイン環境です。使ったことのないPhotoshopユーザ(ないしはPhotoshopプラグイン互換の画像処理ソフトユーザ)は一度遊んでみると良いかもしれません。
また、表計算アプリとの連携や鳥瞰図表示のプラグインもついている……というテキトーな機能てんこ盛り、の環境です。Photoshop Elementなんかで使うこともできますので、画像処理で遊んでみたい人は一度使ってみても良いかもしれません。いつものように、SYSTEMコールもできるプラグインなので、つまりは何でもし放題のプラグイン環境です。使ったことのないPhotoshopユーザ(ないしはPhotoshopプラグイン互換の画像処理ソフトユーザ)は一度遊んでみると良いかもしれません。
2008-06-10[n年前へ]
■「他人の気分推定機」と「カルマンフィルタ」 
よくある制御工学の教科書がわかりにくい大きな理由は2つあると思う。まずひとつ目の理由は、読者としての私の理解力が低く、頭が悪いという根本的な問題である。そして、もうひとつの理由は、すでに綺麗に証明された問題を、その綺麗な数式の記述・順番で説明していく、という本が多いことにあると思う。その綺麗な証明にいたるまでの試行錯誤の説明がないと、「そういった数式をなぜ導出するに至ったか」といったことや、「その数式を使って、本来(さらにその先)何がしたいのか」ということがわかりにくくなってしまうと思う。ひとことで言うと、エレガントな証明とわかりやすい説明は違う。少なくとも、私のようなおばかな人間にとっては、そう思う。
制御理論の教科書で、何だか読み飛ばしたくなる「状態量オブザーバ」「カルマンフィルタ」なども、それを例えるなら、単に「他人の気分推定機」に過ぎない。一見難しそうな言葉を使って書いてある数式も、そこに書かれている内容を例えていくなら「"直接知ることができない"他人の気分をいかに正しく安定して推定するか、というフィードバック機構」に過ぎない
「他人の気分・他人の心の中」というものは、(少なくとも現在の技術では)外からは計り知ることができない。そこで、「この人はこんなことを考えているのかな?」と想像(推定)しながら話をしてみる。ところが、「その人の顔色や話す言葉からは、何だか”その人の気分”が私たちの想像とは違う」という感じがする。……それなら、「この人は”もう少し気分が悪い”と考えておいた方が良さそうだ」とか、その逆に「この人は想像していたより”少し気分が良い”らしい」と想像上の「他人の気分・他人の心の中」をちょっと訂正するのが「オブザーバ」である。
そして、その人が結構ウソをつきがちだったりした場合の「他人の気分・他人の心の中推定機」が、カルマン・フィルタだ。「この人はこんなことを言っているけれど、(こういったジャンルの話では)この人は言うことと・心の中とこの人は違うことが多いから、ちょっと言葉を聞き流し気味に捉えておいた方が良さそうだ」といったことを考えつつ、「他人の気分・他人の心の中の推定量」を(より正しそうな)フィードバック補正をするのがカルマン・フィルタである。
それだけのことなのだけれど、教科書の数式の羅列を追いかけている最中には、そういう景色が見えてこないことが多いように思う。そんな不満足の解決をするためには、「歴史の教科書のように試行錯誤の過程に満ち溢れた、決して”エレンガントな証明本”でないような教科書」をどこかで手に入れて読んでみるしかないのだろうか。……それとも、根本的な一番目の原因「読者としての私の理解力が低く、頭が悪い」ということを直すことしか解決策はないのだろうか。
2008-06-22[n年前へ]
■ホッケー・パックの飛び方のナゾ 
(チューインガムで作った)ラトルバックではないけれど、実際に再現させることは簡単にできるのだけれども、その動きの仕組みを説明しようとすると結構難しいことということが多い。いや、多いどころか、上手く説明できないことばかりが世の中には満ちているように思う。単純に言ってしまえば、「実際に起こる現象を理解・説明する力」というのが不足気味なわけだ。
そんな、「実際に再現させることはできても、その動きの仕組みを説明しようとすると結構難しい」ことの一つが、「ホッケー・パック」の飛び方だと思う。平面の上に置かれた扁平円板を叩くと、それが上に飛んでいく仕組みをきちんと説明しようとすると、これが結構難しい。ゴルフボールのように、ピンや芝生の上に浮いている状態の物体を打つのではなくて、あくまで摩擦抵抗の低い平面の上にある扁平円板を叩くのに、パックが浮かんで飛んでいく減少を定量的に話すのは、なかなかに難しいように思う。
パックがホッケー・スティックのブレードの先で回転することで(決して小さくない)回転モーメントを持ち、その回転モーメントがあることが前提で、スティック・ブレードの下部がホッケー・パック下部を押し、ブレード面を転がり浮かぶようにして、クルクル横に回転しつつ、パックが斜め上に飛んでいく…というような説明はできても、それを数式を書きながら、単純な形で説明してみろと言われたら、言葉に詰まってしまうに違いない。(参考動画)
ヘロヘロと縦回転をしながら情けなくパックが飛んでいってしまうことが多いように、頭の中で計算をしようとしてみても、どうしても「ヘロヘロと縦回転をしながら情けなくパックが飛んでいってしまったりする」のである。現実にも、あるいは、頭の中のシミュレーションでも、鋭くゴール上方隅に決まるようなシュートが打てたら良いのだけれども。
2008-06-28[n年前へ]
■「Mathematica開発者のウルフラム」と「ファインマン」 
 今週頭に「数式処理アプリケーションのMathematicaが最初にリリースされてから、今日で20年たちました」と、開発者Stephen WolframからMathematicaユーザにメールが送られてきた。スティーブン・ウルフラムが28才の時の1988年の6月23日にMathematica 1.0 が出荷されたのである。
今週頭に「数式処理アプリケーションのMathematicaが最初にリリースされてから、今日で20年たちました」と、開発者Stephen WolframからMathematicaユーザにメールが送られてきた。スティーブン・ウルフラムが28才の時の1988年の6月23日にMathematica 1.0 が出荷されたのである。
For twenty years we've pursued our long-term vision for Mathematica.
Mathematicaは結局のところ、パターンマッチングを延々と行うプログラムである。データベースに登録されているパターン・規則にもどづいて、与えられた数式を置換していくことにより、Mathematicaは解(や所望の結果)を得る。
 ところで、「ファインマン物理学」で有名なR.P.ファインマンはカリフォルニア工科大学で1983年から1985年までの間、計算機科学の講義(ファインマン計算機科学)をしている。その頃の学生がスティーブン・ウルフラムである。
ところで、「ファインマン物理学」で有名なR.P.ファインマンはカリフォルニア工科大学で1983年から1985年までの間、計算機科学の講義(ファインマン計算機科学)をしている。その頃の学生がスティーブン・ウルフラムである。
ファインマンは「科学とは何か」の中で、「数学とはパターンにすぎない」「数学とはパターンを探すことだ」と端的に短く書き表している。この言葉を思い起こしながら、(おそらくそんな言葉を聞いていただろう)彼の学生でもあったウルフラムが「パターンマッチングによる数式処理アプリケーション」を商品化し市場に広まらせたのだ、と考えてみると何だか「面白い繋がり」を感じる。そんな繋がりを思い浮かべながら、Mathematicaの20年を集めたスクラップブック を眺めてみると、きっと楽しいと思う。
I'm looking forward to the next 20 years and hope that you'll continue to follow Mathematica on this exciting journey.
-- Stephen Wolfram
2008-07-09[n年前へ]
■光スペクトル操作用のMathematicaライブラリ 
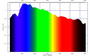
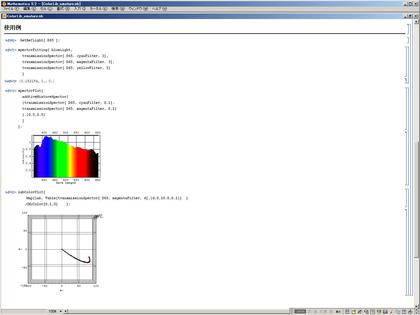 以前、Mathematicaの演習用に作った「スペクトル操作用Mathematicaライブラリ」を少し直したので、ここ(”ColorLib_amature.nb”に置いておきます。以前作ったものと同じく、スペクトル・データをリストのような離散データではなくて、関数として(純関数=無名関数として、あるいは、明示的な関数として)取り扱うという点が特徴だと思います。「(せっかくMathematicaで解くのですから)解析的に解く」「使用者には離散化・数値計算など、面倒くさい汚い部分は見せない・見たくない」という方針で作ったものです。
以前、Mathematicaの演習用に作った「スペクトル操作用Mathematicaライブラリ」を少し直したので、ここ(”ColorLib_amature.nb”に置いておきます。以前作ったものと同じく、スペクトル・データをリストのような離散データではなくて、関数として(純関数=無名関数として、あるいは、明示的な関数として)取り扱うという点が特徴だと思います。「(せっかくMathematicaで解くのですから)解析的に解く」「使用者には離散化・数値計算など、面倒くさい汚い部分は見せない・見たくない」という方針で作ったものです。
以前のものからの変更点としては、"spectorPlot"や"labPlot""labColorPlot"など、関数名のMathematicaの命名規則に合わせた変更、加法混色・減法混色用関数の追加・グラフ表示関数の追加・バグ修正といったところです。
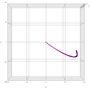
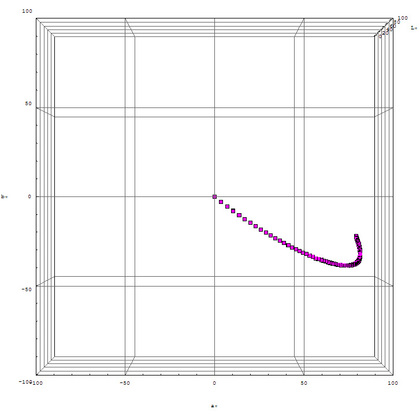 最初のラフスケッチが、絵画の原理を自分なりにおさらいするためのものだったので、濃度変調・面積変調などを扱おうとする場合には、比較的簡単に・気持ち良く作業ができると思います。たとえば、下記のようなコードを書けば、D65光源のもとで、赤紫色の絵具を重ね塗りしていったときの色の具合を CIE Lab 空間で眺めたりすることができます。
最初のラフスケッチが、絵画の原理を自分なりにおさらいするためのものだったので、濃度変調・面積変調などを扱おうとする場合には、比較的簡単に・気持ち良く作業ができると思います。たとえば、下記のようなコードを書けば、D65光源のもとで、赤紫色の絵具を重ね塗りしていったときの色の具合を CIE Lab 空間で眺めたりすることができます。
labPlot[
Map[lab,
Table[transmissionSpector[D65,
magentaFilter, d],{d,0,10.0,0.1}]
]
];
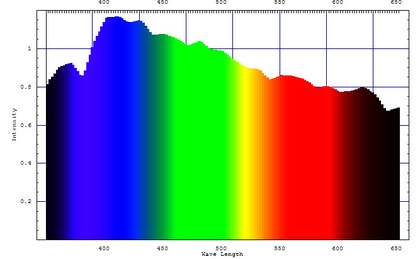 また、白色光照射時に黄色い絵具を塗り拡げる面積を増やしていった場合の反射光スペクトル変化をアニメーションとして作成・グラフ表示するコードはこんな感じです。"addtiveMixtureSpector"は加法混色用の関数で、"transmissionSpector"は減法混色用の関数です。お遊びソフトですが、色々遊ぶこともできるかもしれません。
また、白色光照射時に黄色い絵具を塗り拡げる面積を増やしていった場合の反射光スペクトル変化をアニメーションとして作成・グラフ表示するコードはこんな感じです。"addtiveMixtureSpector"は加法混色用の関数で、"transmissionSpector"は減法混色用の関数です。お遊びソフトですが、色々遊ぶこともできるかもしれません。
Map[spectorPlot,コードを書く際に、Mahematicaで数式と文字列をシームレスに取り扱うことができたなら、もっと簡単に関数が書けるのにとも感じました。しかし、そういった感覚になるときは、たいていの場合「その道具の使い方・その道具を扱うプログラミングスタイルが間違っている」ことが多いものです。というわけで、Mathematicaプログラミングをまた勉強しなおしてみよう、と思ったのです。
Table[
addtiveMixtureSpector[
{whiteLight,
transmissionSpector[whiteLight, yellowFilter, 1]},
{1-r, r} ],{r,0,1,0.1}]];