hirax.net::Keywords::「方程式」のブログ

■「色んな単位」と「”メガ”+”乳”=”メガ乳”という方程式」　

　「メガ乳」という言葉の発明者と会ったことがある。マクドナルドのハンバーガー「メガ・マック」などをきっかけに、メガ×○△といった言葉を良く聞くようになったが、最近では、この「メガ乳」という言葉が使われることも多いらしい。「100万倍」を意味する科学用語・単位「メガ」が、こういった用途に使われるということに、奇妙な新鮮さを感じる。

　科学離れが語られる今日この頃だけれども、こんなことにも「100万倍＝メガ(mega)」という科学用語が使われているのだ。科学と日常生活の距離は、ずっと昔からそうだったように、（もちろん、近いとも限らないが）決して遠くはないのである。

　よくよく眺めて見ると、「メガ」＋「乳」＝「メガ乳」という言葉は、案外良い組み合わせだと思う。たとえば、「メガ乳」の10億倍を意味する「1000兆倍＝ペタ(peta)」では、「ペタ」＋「乳」＝「ペタ乳」になってしまう。これでは、妙にフラットな印象をかもし出してしまうように思う。それなら、むしろメガの10万分の１の「10倍＝デカ(deca)」の方が迫力を感じるような気がする。

　単位系を眺めているうちに、結構気に入ったのが「1兆分の1＝ピコ(pico)」だ。「乳」という言葉の接頭語としては、「ピコ」も結構似合うような気がする。

■「爆乳でなくなったら歩けない」を科学する　

　「爆乳」という言葉の名付け親と「メガ乳」という言葉の名付け親と話をした時に、「新鮮に聞こえるが普遍的にも聞こえる」話を聞き、面白さを感じた。そんなことを感じた話のひとつが、こんなことである。

　（IとかKカップとかいった爆乳の女優さんの多くが言うことには）「バストが小さくなったら、歩き方がわからない」「もう歩けなくなってしまうかもしれない」

　2kgほどの重量物を胸部に二つも可動する状態で歩こうとしたなら、「重量物の揺れ・振動」を抑えつつ、それでも抑えきれない重量物の揺れと共存した歩き方にならざるをえないはずだ。つまりは、大きなバストがあること前提の歩き方になっているに違いない。だから、「バストが小さくなったら、歩き方がわからなくない」ということになるのだろう。

　ところで、可動する重量物、端的に言えば・揺れるバストは、下に描いたようなバネ・ダンパモデルとして単純にモデル化することができるだろう。つまり、その図の下に書いた微分方程式で表されるダイナミック・システムである。あるいは、それを伝達関数モデルにまでしてしまえば、つまりはさらに下に描いた「２次遅れ要素」である

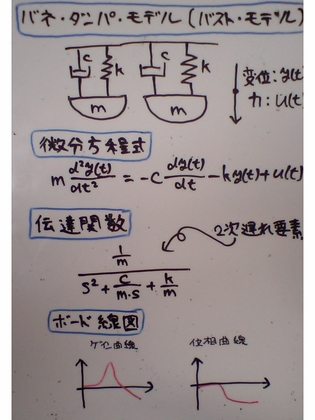
　電気のRLC回路（発振回路）なども、上の微分方程式と同タイプの式で表現される。そして、発振回路でコンデンサの容量（Ｃ）がいきなり小さくなってしまった場合などは、当然ながら発振周波数も変わり、その結果、回路の動きは大きく姿を変えることになる。つまり、「容量が小さくなってしまったら、（それまでの動かし方では）回路が動かなくなってしまう」という状態になるわけだ。

　つまり、上に描いた「メガ（爆）乳」を表現したダイナミック・システムと電気回路の間には、類似性（アナロジー）があって、それらは共通の普遍性を垣間見せるわけである。

　だから、実は、電気工学や機械工学のエンジニアたちこそが「爆乳の女性人たちが経験的に会得した歩き方の工夫」の一番の理解者になったりするかもしれない、と思ったりもするのである。「そうそう部品の定数がいきなり変わったら困っちゃうよね」と大いに共感できそうなきもするのだ。……もちろん、そんな妄想に「そんなわけない」とすぐに突っ込みたくもなるのだが。

■「スペクトル操作Mathematicaライブラリ」で動画を作る　

　光スペクトル操作用のMathematicaライブラリで、スペクトル変化の動画を作ると、こんな感じになります。Map　も　spectorPlot　も　Table も addtiveMixtureSpector　も whiteLight も cyanFilter も・・・どれも「関数」です。addtiveMixtureSpector　や whiteLight や cyanFilter は「関数を返す関数」で、Map などは関数を引数にとる関数です。Mathematica でコードを書いていると、なぜか自然に関数を重ね合わせていくような書き方が気持良くなってきます。

Map[spectorPlot,
　Table[
　　addtiveMixtureSpector[
　　　{whiteLight,
　　　transmissionSpector[whiteLight,
　　　cyanFilter, 1.0]}, {1-r,r}]
　,{r,0,3,0.05}]]

　それで、今この瞬間の悩みはMathematicaで"spectorFitting[targetSpector_,usingSpectrum]"というような関数をどうやって書くか、ということです。targetSpector は、任意のスペクトルを表現する関数で、usingSpectrum は「スペクトルを表す関数群」で要素数は任意のリストです。usingSpectrumを使いtargetSpectorをどのように表現するかを、最小二乗近似で最適解をNMinimize で解くというのが、そんな関数を作るときの定番の手順なのだろうと思います。つまり、方程式と制約条件を動的に作成し、それをNMinimize で解いた結果を返す、という具合です。

　さて、この　spectorFitting という関数はどう簡単に書くことができるものでしょうか。Mathematicaは変数名と文字列を明確に区別する割に、見た目ではまったくその違いがわからないのが面白いところ（同時に苦労するところ）かも、と思ったりしたのです。

■エクセルでシミュレーション Vol.1 [静電界準備 編]　

　「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは（私たちのような勉強世界からの REST OF US にとっては）とても素晴らしいと思います。

　ところで、現在では”表計算プログラム＝マイクロソフトのエクセル(Microsoft Excel)”だと考える人も多いことでしょう。だから、上に書いたことを言い換えれば、「エクセルでシミュレーションをする」のは、とても楽しい勉強になるということになります。

　自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備（事前確認）」をしてみました。

　まず、静電場を記述するポワソン方程式をテーラ級数展開することで離散化し、差分方程式に変えてみます。２次元世界を離散化するということは、エクセルの表がそうであるように「世界（画面）をセルで分割する」ということです。

　この離散化された後の差分方程式は、つまり「セル間の計算（関係）式」ですから、「２次元静電場を記述するポワソン方程式を、（エクセルの）セル間の計算式で解く」ことができることになります。

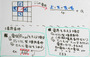
　上で（x,y座標空間での）差分方程式にしたものを、さらにエクセル（表計算ソフトウェア）で解くときのやり方を図解したものが下の図です。「ある点の電位（φ）は上下左右の電位の平均にその点の(係数がかかった)空間電荷を加えたもの」になっているわけです。

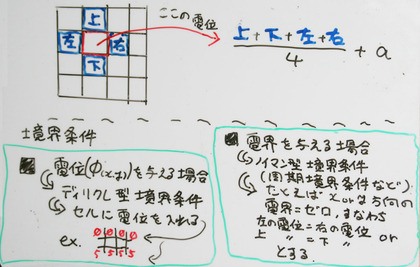
　また、2種類の境界条件（電位を指定するディリクレ条件/電界を指定するノイマン条件）をどのようにエクセル上で処理するか、というのが下の部分になります。

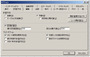
　こういったセルの値が「（そのセル自身を含む）セル間の関係式」で表わされるような計算式を解くためには、エクセルの設定で「反復計算を行う」という設定を有効にしておく必要があります。エクセルのバージョンによってその設定メニュー場所は違いますが、たとえば、下の画面はExcel 2003の設定ダイアログの例です。

　以上で、「静電界を記述するポワソン方程式をエクセルで計算するための前準備（事前確認）」が終わりましたから、次は実際に「身近な静電界」をエクセルでシミュレーション計算してみたいと思います。

■エクセルでシミュレーション Vol.2 [静電界計算の動画 編]　

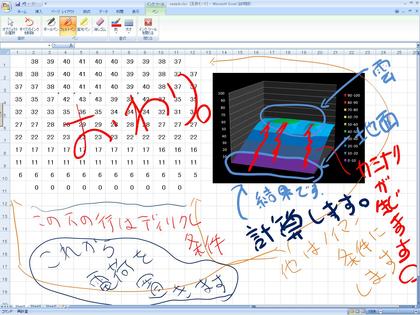
　エクセルでシミュレーション Vol.1 [静電界準備 編]で、（ポワソン方程式で表わされる）静電場の計算をエクセルでする準備作業ができたので、実際にエクセルで静電界計算をしてみました。どのような状態を計算してみたかというと、「夏の空に帯電した雲が生じた時の、地面から空へ向かう空間の断面の電場」の状態です。地面をグラウンド＝０Vとして、空に電荷を帯びた雲が浮かんでいる状態を計算してみました。エクセルを使って、その計算シミュレーションをゼロから作り上げ、結果を描き終わるまでの8分弱の動画が下のものになります。また、mpeg形式の動画ファイル(65MB)もここに置いておきます。

　夏の雷雲は負の電荷を帯びていることが多い、といいます。上のシミュレーション条件では、（動画を見ればわかるように、式後半に正電荷を入れましたから）雲の部分に正電荷を帯びさせましたが、そこは正負をひっくり返せば良いだけです。夏の日、暑い午後、都会や田舎の空に雷雲が見えてきたら、そのときの電場シミュレーションを（突然の落雷による停電に気をつけながら）PCのエクセル上でしてみるのも、気分転換になるかもしれません。