2008-07-21[n年前へ]
■エクセルでシミュレーション Vol.4 [定常理想流体準備 編] 
夏の午後の空に浮かぶ雷雲を見ながら、昨日は静電界シミュレーションをマイクロソフト・エクセルで手軽にしてみまたわけです。暑い夏空をシミュレーションしてみたので、今度は、冷えた湧水が地下で流れているを眺めてみたくなりました。そんなシミュレーション計算をするために、理想流体の「定常的な流れ場」を表計算ソフトで解くための前準備を、今日はしてみました。
というわけで、そのためのラクガキが下の画像になります。
ここまでくると、もう「エクセルでシミュレーション Vol.1 [静電界準備 編]」と同じです。ポワソン方程式とラプラス方程式は、端的に言ってしまえばほとんど同じなので、後は「２次元の（ポテンシャル）流れ場を記述するラプラス方程式を、（エクセルの）セル間の計算式で解く」ことができることになります。
2008-07-26[n年前へ]
■Simulinkで”日焼け対策”を最適化 Vol.1 [はじめに 編]
先日、Mathematicaで肌の色や日光の色スペクトルを表現するためのライブラリを作り、いくつか計算をしてみました。また、昨日は、「日焼けに影響を与える日照時間」の変化・「気温の変化」「化粧品の商品切り替え時期」「日焼け対策を行う時期」について考えてみました。
そんなことを考え出すと、究極の”日焼け対策”・至高の”日焼け対策”はどういう風にすれば良いだろうか、という技術的な興味が湧いてきます。もちろん、外に一切出ない・顔には紫外線反射膜をコーティングする、といったような対策もあるわけですが、そんな対策をしても「そんな毎日でいいのか？」という疑問を感じるに違いありません。やはり、色々な観点を含めた上で、それらの観点を少しづつ満たすような”日焼け対策の最適化”を考えなければならないように思われます。
そこで、Simulinkを使って、（動的なシステムのモデル化・制御システム構築・プロトタイピングを簡単に行うことができる）MATLAB社のSimulinkで”日焼け対策”を最適化に挑戦してみたくなりました。そこで、今日はまず[はじめに]ということで、平均日照時間と平均気温をSimulinkでグラフ表示してみました。
とりあえず、下の微分方程式のように平均気温(TEMP)の変化は平均日照時間(SUN)に比例するとおくと、
d TEMP /dt = SUN平均気温は平均日照時間を積分したもの、ということになります。そんな関係をSimulinkでモデル化し(数値はまだ合わせていません)、グラフ表示してみたのが下の図です。気温が日照時間に対する「位相遅れ」を持っていることがわかります。
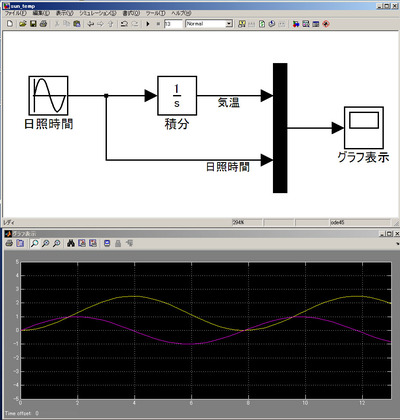
・・・と、ここまでは当たり前の結果ですが、こんな感じで「日焼け対策の最適制御」について色々考えていこうと思います。
2008-07-30[n年前へ]
■「道具」と「文化」
「道具」は「文化」の要素の一つだ。しかも、それは比較的大きな要素である。「2001年宇宙の旅」で棒という道具を手にした猿が、その棒をついには宇宙ステーションという道具に変えたシーンが象徴的であるように、道具は人の生活スタイルに大きな影響を与え、そしてその生活スタイルは考え方・感じ方にさらに大きな影響を与える。つまり、道具は文化に影響を与える。
「フレームワークと異文化論」が面白い。
「Railsって一本道のイメージなんでしょうか。これにそって作ればWebアプリケーションが不安定にならずに完成するんでしょうか」
「私にとって“レイルズ”のイメージはこれなんです」といいながら、東京近郊の複雑な路線図を大写しにすると、会場は大爆笑に包まれた。
この会場に来るためにどの路線を使ったら良いのかを考えたときに、さまざまな選択肢があったと思います。……そんなにレイルに縛られなくてもいいんじゃないでしょうか
「線路」と「人生の方程式」ではないけれど、レール(線路)なんか一本じゃないし、だいたい設計した線路は実際の線路とは全然違ったりする。それが人生ではとても普通のよくあることで、それが大変さでもあるし、楽しさでもある。
多少なりとも他の文化を知らないと、ひとつの文化の姿を実感することはできない。他のものとの差異を見て、初めて自身の特徴が見えてきたりするからだ。道具の特徴を知るためには他の道具を知ることが役立ち、道具が文化に強く影響を与えるのだとしたら、そして文化が人の生活そのものだとしたら、（一つの道具を使えるようになった上で）他の道具を眺めてみることは、人の生活に大きな影響・大きな広がりを与えるに違いない。
2008-08-05[n年前へ]
■エクセルでシミュレーション Vol.6 「夏にフライパンで卵焼き 編」
「表計算ソフトウェアでシミュレーションをする」という講習を見続け、何よりも面白かったのが「非定常の３次元熱計算を簡単に、それでいて、できる限りきちんと計算をやってみよう」という（I氏が講師の）シリーズです。
一次元非定常の熱拡散問題を陰的解法で解く「熱伝導方程式を表計算ソフトで解くサンプル」は多いように思いますが、「非定常の３次元熱計算を表計算ソフトウェアで解く簡単にやるテクニック・サンプル」は、（私は）他では見たことがありません。しかも、このシリーズは本当に簡単で、なおかつ、できる限り精度を保証して解く、というとても稀有な例です。「難しい問題」を「簡単に」「きちんと」「精度を保証して」解く…といったようなものたちは相反することが多いわけですから、そういったものを兼ね備えているというのは、とても珍しいと思うわけです。
下の例は、そのテキストを利用して、陽的解法で安定性条件が成り立つようにして、「夏の朝に、角型フライパンをコンロで加熱した際のフライパン温度分布」を計算した例になります。ある厚みを持ったフライパンが、コンロのガスの炎が当たっている部分が「100度」に（熱）されているような条件の時、フライパンの温度分布が時々刻々と変わっていくようすを計算した結果です。こんな計算をエクセルで数回しておけば、「美味しい卵焼きを作るための最適条件・最適なやり方」を導き出すことだってできるかも、と思わされるのです。エクセル上で、フライパンの厚みや熱伝導度を変え、コンロの炎分布を色々変えてみたりしたならば、究極・至高の卵焼きを作るための最適・必須条件が見つかるかもしれない、と楽しく思えてきたりします。
ところで、この「非定常３次元熱計算」のエクセルシートは、本当に簡単に作ることができるのですが、その一方で、このシートは（簡単なのに）実に巧みに作られています。だからこそ、「難しい問題」を「簡単に」「きちんと」「精度を保証して」解くことができるわけです。
その「巧みさ」を紐解いてみると、これが実に綺麗なパズルのようで、とても面白いのです。・・・というわけで、その「巧みさ」「面白さ」についての感想文は、また後ほど書いてみようと思います。
2008-08-06[n年前へ]
■エクセルでシミュレーション Vol.7 「吉野家の法則 編」
「安い」「早い」「旨い」を兼ね備えたものは売れる、というのが「吉野家の法則」の第１法則である。けれど、それら３つのことは相反することが多いために（「吉野家のジレンマ」）、それら３つのうち最低２つのものがあれば売れることが多い、というのが「吉野家の法則」の第２法則だ。
「表計算でシミュレーション」というお題で、この吉野家の法則の「安い」「早い」「旨い」を考えてみよう。
まずは「安い」である。それを言いかえれば、「簡単に手に入れることができる」ということだ。まず、「表計算でシミュレーション」はこの「安い」という条件を非常に上手く満たしている。
- 表計算ソフトウェア・エクセルを持っている人は多いから、必要な道具を手に入れることが簡単である。
そして、次の「早い」である。これを言い換えてみると、「すぐにできる」ということだ。「表計算でシミュレーション」をする場合には、たとえば、時間的に変わらない（定常な）問題であれば、比較的簡単に計算シートを作ることができる。だから、すぐにできるようなシートを作ることができる範囲内では、「表計算でシミュレーション」というものはとても「早い」のである。ただ、あくまで「比較的簡単に計算シートを作ることができる範囲内では」ということが少し尾を引くのである。
問題は、最後の「旨い」である。これは、多分、２つの意味がある。ひとつは単純に「実利的なメリット」だ。つまり、たとえば「すぐに仕事に使える」というようなことになる。そして、もう一つは「心としてのメリット」である。それは、たとえば「面白い」「意外だ」「へぇ～」といったような感覚を得ることだと思う。
先の「比較的簡単に計算シートを作ることができる範囲内では」という先の制限は、これらふた種類の「旨い」と相反することが多い。それが、「表計算でシミュレーション」における吉野家のジレンマなのである。すぐに仕事で使うためには、「定量的に計算結果が正確である」ようなことが要求される。しかし、そうしようとすると、シートを作るのが面倒だったりして、「早い＝すぐにできる」ではなくなりがちになってしまう。
また、「早い＝すぐにできる」ようなものは、比較的「当たり前」の計算結果が出てくる。たとえば、等方・等質的な空間でラプラス方程式で解いた静電界計算結果などは、「見た目にいかにも”自然”なもの」になる。それが”自然”なのだから、それでいいではないか、とも思う。しかし、その一方で、それでは意外性も何もなく、「へぇ～」「面白い」という感じを受けないのである。
このように、「安い」「早い」「旨い」という吉野家提供の三つの評価軸から、「表計算でシミュレーション」を眺めてみると、「表計算でシミュレーションをする講習」が持ちがちな悩みが見えてくる。「早い」と「旨い」の兼ね合いの難しさが見えてくる。
昨日の『エクセルでシミュレーション Vol.6 「夏にフライパンで卵焼き 編」』の場合は、腕が良いシェフ（I講師）吉野家の法則の３評価項目を見事に上手く兼ね備えているのである。
」など。