2001-11-22[n年前へ]
■あなたと見たい、流星群 
同じ流星が見える距離
「しし座流星群」が美しく盛んに空を彩った翌朝、Fast&FirstのBBSをぼんやりと眺めていると、「アナタとみたい流星群」と題した
「僕たち距離は離れているけれど、同じ星(月)を見ているんだね」という書き込みを見かけた。思わず良い話だなぁ、と見入ってしまった。
なんて会話をする二人がいます。だけど、一体離れている距離が何km位までなら同じ流星を見ることができるのでしょうか?
今年の「しし座流星群」のようなきれいな流星群を、深夜同じ場所に佇んで二人で一緒に同じ流星を眺める人達も多いだろうが、離れた場所から、それでも同じ流星を眺めている二人もいることだろう。「そんな遠く離れた二人が、同じ流星を眺めることができるとしたら、それはどの程度の距離までなのだろう?」という「同じ流れ星を眺めることができる二人の距離」だなんて、とてもロマンティックでとても面白い話だなぁ、とその書き込みを眺めながら思った。そして、これはいつか考えた「地平線問題」と同じだなぁと考えて、だけど何故だか少し切ない話だなぁ、とも感じた。
だから、とても興味を惹かれたのだけれど、その切なさのせいか、ただぼんやりとその話を眺めていた。すると、すぐに「今日の必ずトクする一言」のKOROKAN氏が
これは計算が可能ですね。…流星の輻射点から地球に接線を引きます。そうすると、と簡潔な答えを書きこまれていた。暗算で片付けるところはやはりさすがスゴイなぁ、なんて感心していると、それとほとんど同じ頃、hirax.netの「ぐるぐる検索」にも、元の質問を書き込まれていた方から、
地球の中心、輻射点、接線が地球に接する点の直角三角形になりますね。…(中略)…これに地球の半径をかけると1118kmと出ました。
つまり半径1118kmの範囲が輻射点から見えることになりますから、(二人の距離としてはその二倍の2000kmで)おそらく東京−福岡、東京−札幌の遠距離恋愛なら見えるかも。
あなたと私、離れていても同じ星を見ている。何kmの距離まで離れていても同じ流星を二人は見ることができるのでしょうか? (F&Fの掲示板に書きこんだ内容に同じです。)という検索メッセージが送られてきた。そして、さらに
とても好きな女性が私の住むミネソタから約1000マイルほど離れたオハイオに住んでいまして、彼女に獅子座流星群の話をしながらこの話を思いついたのです。ちょうど1000マイルだったらギリギリって感じかもしれない?遠く離れた場所でも、同じ流星を見ることができるかもしれない?という話の発端を読みながら、私もちょっと落書きをしてみた。
KOROKAN氏が簡潔に書かれていた答えをもう少し言い換えると、「私たちが流星を見ることのできる距離」は「流星の地平線」と同じだ。私たちが流星を見ることができるのであれば、逆に流星からも私たちが見通せることになるのだから、「地表に立つ私たちが流星を見通せる距離」=「流星が地表に立つ私たちを見通せる限界」、ということであって、それはすなわち「流星の地平線」そのものということになる。もちろん、本当はもっと色々なことを考えなければならないわけだけれど、とりあえずはこんな大雑把な計算でも十分だろう。
●流星の発光点  |
以前、地平線までの距離を計算した
でやったものと同じく(KOROKAN氏が書かれていたことと同じ)、灰色の直角三角形に着目してやると、流星の発光点の高度がわかれば、あとは地球の半径=約6400kmを用いれば、流星の地平線までの距離は簡単に計算することができる。 流星の発光点の高度は理科年表をめくると、次のような表が載っていて、大体70km〜130kmの間であることが判る。その高度差を100kmほどの長さにわたって、光りながら駆け抜けて行くのである。
 |
そして、「流星の発光点の高さY」を変えた場合の、流星から見渡せる距離(=流星の地平線)を計算してみたものが次のグラフになる。この「流星から見渡せる距離」がつまりは「流星を見ることができる最も長い距離」になる。
 |
先の「流星の発光点の平均高度」として約70km〜130kmという値を使うと、先にKOROKAN氏が書き込まれていたように1000km前後という数字になるわけである。で、流星の発光点(輻射点近く)を挟んで遠く離れたところに住む二人であれば、その二人の距離が1000kmの二倍で2000kmの距離までは同じ流星が見える、ということになる。
だけど、これは理想的な話で、現実の話ではない。
実際にはそんなわけにはいかない。私達が住むほとんどの場所は、海原の真中や高い山の頂きじゃない。私達が流星を眺める場所はビルや鉄塔に囲まれたマンションのベランダだったり、あるいは木々や小高い山が周りを囲む小さな公園だったりする。少なくとも、地平線の果てまで見通せるような場所で眺める人なんかほとんどいないだろう。流星を眺めようとするほとんどの人達がいる場所は、上に広がる空しか見えなくて、地平線近くの空なんか見えない場所だとう思う。きっと、せいぜい天頂から60〜70°位の角度までしか空を見通せないに違いない。
だとすると、さっき計算のときに着目した「灰色の直角三角形」は少し変えてやらなければならない。人の視点での地球への接線をひくのではなくて、もう少し天頂側へ角度を振ってやる。すると、先の「灰色の直角三角形」は下の図のように「青色の三角形」に変化することになる。
●流星の発光点  |
そして、先と同じようにこの三角形に注目しながら、「限られた空の下」に住む現実の私達が見ることのできる流星までの距離を計算してみると、下のグラフのようになる。下のグラフで「空を見渡せる角度」が天頂からの角度で90°、すなわち地平線まで完全に見渡せる場合である。つまり、先に計算した「理想的な場合」である。そして、それが1100km程度というのはもちろん先程と同じだ。
 |
このグラフを眺めてみると、天頂からの角度に対しての「見ることができる流星までの距離」は「地平線近く」の場合とそうでない場合とで全然違うことが判るだろう。
「地表面」と「その100km上空の面」というのはほとんど平行だから、天頂からの角度が70°位までは「流星の発光点までの距離」は緩やかに増加していくだけだ。天頂からの角度が70°(というとかなり水平にもう近いが)の時でさえ、「流星の発光点までの距離」はたった200km強である。さきほど見えると思われた1000kmなんて遥か彼方だ。
しかし、天頂からの角度が80°を超え、ほとんど水平間際になってくると、「見ることができる流星までの距離」はぐんぐんと大きくなってゆく。80°で600kmくらい、85°で700kmくらい、そして90°でついに1000kmの彼方の流星まで見えることになる。
ということは、現実の私達、海原の真中や高い山の頂きじゃなくて、ビルや鉄塔に囲まれたマンションのベランダや小さな公園から流星を眺める「限られた空」の下に住む私達は、せいぜい200kmくらいまで離れた場所で光る流星しか見えないことになってしまう。1000kmの彼方の流星なんかとてもじゃないが見えなくて、たった200kmが限界になってしまうのである。
すると、遠く離れた二人が同じ流星を眺めようとするとき、その二人の距離の限界は高々200kmx 2=400km程度ということになってしまう。東京-大阪でも難しいかもしれない。空が本当に天頂近くに限られて、「空が無い」東京のような場所であれば、きっとその距離はもっとずっとずっと短くなるはずだ。新幹線に乗って会いに行くような二人では、同じ流星を眺めることはできないのかもしれない。
だけど、とも思う。先のKOROKAN氏の書き込みは
それに何より、「見ているモノが同じモノ」と信じる力が重要で、それが同じモノか、別のモノかを証明するすべも、否定するすべもありませんなあ。信じる者は救われるというし。という風に締めくくられていた。私も本当にその通りだと思う。さっきの「せいぜい400kmが限界」なんて計算結果は「同じ流星を眺めようとする二人」には全然関係ないのだろう、とも思う。
もしも、遠く離れて見渡せる空が全然重ならないような距離であっても、例えそれが昼と夜ほどの違いになる距離であっても、同じ景色を眺めている二人もいるだろう。また、逆にとても近くにいても同じ景色も流星も眺めることのできない二人もいるのだろうと思う。そんな違いを決めるのは、幾何学的な話じゃなくて、きっと別の何かだ。
そしてまた、流星を眺める私たちの視点から、流星の視点に移動するといろいろなものが見えてくるとも私は思う。「限られた空」の下の私たちの視点がもう少し高く、高度100kmほどまで上がれば、周りではついに流星が輝やき燃える高さになる。ここまでくれば、見渡すことのできる地平線の果てまでは1000kmほどになる。その半径1000kmの円の地表が、その流星の視点から見える世界だ。
そして、その流星の地平線の中にいる人達は、その流星を同時に眺めることができる人達であるが、一体その半径1000km程の領域の中にはどれだけの人達が住んでいることだろう?数千人?それとも、数千万?とてもたくさんの人達がいるに違いない。それは例え、半径200kmの円であってもやはり同じことだろう。その地平線の中にはとてもたくさんの人が住んでいる。
そんな地平線の中の(あるいは外の)数え切れない沢山の人達の中に、同じ流星を眺めようとする二人がいる(それともいない)なんて、やっぱりとてもロマンティックで、やっぱりちょっと切ない話だなぁ、と思う。
2001-12-24[n年前へ]
■サンタが街にやってくる 
複数サンタクロースの巡回問題
簡易に書き直した2011年版もあります。
幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで(高原の診療所なのだから大して違いはないのだけれど)、とても不思議だった。
さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。
知らない人のために書いておくと、「巡回サンタクロース問題(TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが
- サンタクロース研究
- ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )
そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。
まず、始めに問題提起をしてみよう。
「果たしてサンタは一人なのか?」
どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。
そこで、まずはサンタの歴史から調べてみると、Santaさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。
とはいえ、Santaさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか?
また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
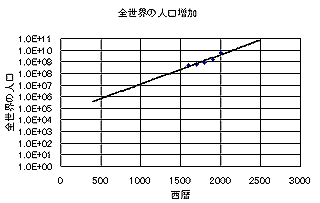 |
St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。
サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。
子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 |
どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。
先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。
そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。
それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
一例として、サンタが1,2,10人の場合を示してみる。
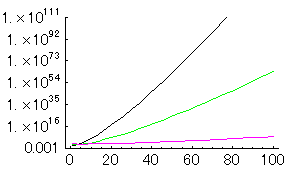 |
このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。
実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。
このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。
ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。
それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。
ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。
もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。
こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。
サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。
2002-01-29[n年前へ]
■「モーニング娘。」を立体にするのだ! 
時間と空間の遠近感ソフトを作る
京都にいた頃、いくつかのホテルでバイトしたことがあった。都ホテル、鴨川沿いのホテル、あるいは、蹴上の辺りにあるホテルなどでベッドメイクやら、会場設営のバイトなどをした。有数の観光地である京都の街中はもう色んな旅館やホテルが数多くあふれているのだから、そんなバイト口は一年を通してあった。
そのバイトに行った色んな旅館の中でも、京都へ行ってすぐにバイトしたホテルは凄かった。その旅館の入り口には「暖簾」がかかっていた。京都の旅館なら、入り口に暖簾がかかっているのは当たり前じゃないの、と言われるかもしれない。しかし、その旅館の「暖簾」はその旅館への車の出入り口に設置してあったのである。
ニホンに憧れ、"A Book of Five Rings"に憧れるスティーブン・セガールのような外国人であれば、「日本人は車ですら暖簾をくぐり、それほどまでに日本人にとって礼節とは大切なものなのデスカ!」と感嘆するかもしれないが、それは少々違う。何しろ、その旅館、いやホテルは名神高速の京都インターチェンジのすぐ横にあった。つまりは、京都インターチェンジの周りのホテル街にあったのである。
いや、ここまで書いても、先のニホンに憧れる外国人なら(今でもそんな人がいたら良いのだが…)、「なるほどなるほど、高速道路と言えば江戸時代の街道デス。ツマ〜リ、高速のインター周りのホテル街は江戸時代で言えば街道の宿場町なのデスネ!」とやはり感嘆するかもしれない。そんな感嘆と感動が的を射ているかどうかはともかく、とにもかくにも一風変わったバイト先だった。
そして、そのバイト先にはいくつも私の好奇心をくすぐるものがあったのだが、そのうちの一つが「立体テレビ」だった。その旅館ホテルには、離れのような作りの特別室という部屋が二部屋ほどあり、特別室には「立体テレビ」なるものが設置してあったのである。といっても、その「立体テレビ」は何か部品が足りないのか、あるいは二十四時間故障中だったのかよく判らないのだけれど、とにかくその「立体テレビ」が動いてるのを見たことはなかった。動いているのを見たことが無く、どんなものだか判らなかったから、なおさら想像力を刺激したのである。もちろん、そのホテルの業種がらどんな番組がテレビから飛び出してくるのかも興味があったのも確かだ。
で、先週どこかで流れていた「モーニング娘。」の音楽を聞いて、何故かその「立体テレビ」のことを思い出した。何故かは判らないのだけれど、思い出してしまったのだからしょうがない。しょうがないから、そんな「立体テレビ」を自分で作ってみることにした。といっても、立体テレビで表示するための特殊なビデオ素材などしか見ることができないのもツマラナイ話なので、普通のビデオ(= 2Dビデオ)を勝手に立体化して、その立体ビデオを見ることができるようなものを作ってみることにした。
ビデオの立体化の原理はとても簡単、単に「時間軸と空間軸を少しばかりシャッフルするだけ」である。
人間が視覚から立体感を得る原因の一つが左右の目で見る景色の違い、すなわち両眼の視差である。その両眼視差を利用して、立体感を付加してやるのである。つまり、動画の各瞬間の画像を右目用と左目用の二つの画像に分けて、その二つの画像に少しばかり差をつけてやることで、両眼視差を人工的に与えれば良いのである。
といっても、「動画の中のある瞬間の画像」を右目用と左目用に分けた二つの画像の間に「少しばかりの差をつける」といっても、そんな画像を作るのはそんなに簡単ではない。そこで、ちょっとこんな風に考えてみるのだ。「動画の中のある瞬間の画像」と「少しだけ差がある画像」はどこかにないだろうか?もし、そんな画像が何処かにあるならば、その画像をちょっとばかり拝借すれば良いだけの話なのである。そんな画像は果たしてあるのだろうか?
そう、そんな画像はとても近くにある。答えは簡単、「動画の中のある瞬間の画像」の「少しだけ時間的に差がある瞬間の画像」が探している答えなのである。「動画の中のある瞬間の画像」と「その次の瞬間の画像」は「ほんの少しだけ色々な位置が違ってはいるけれど、だけど全体的にはほとんど同じような画像」なのである。そんな画像を両眼で別々に眺めてみれば、適度の両眼視差により立体感を得ることができるハズなのである。
というわけで、普通の動画像に対して、「時間的に前後に並んだ二つの画像を空間的に左右に並べて」、平行法で眺める動画像に変換するソフトウェアを作ってみた。それが、これperspective.exeである。もちろん、いつものように動作保証一切無しのアルファ版ソフトだ。
perspective.exeの動作画面は下のようになる。"File Open"で動画像を開いて、"Make3D File"で立体動画像を作成・保存することができる。 |
例えば、まずは素材として以前作成した「モンローウォークの動画」を再生している画像を下に示してみよう。Real形式で圧縮したオリジナル動画はこちら(original.rm 9kB )である。
 |
この動画をこのperspective.exeで処理するとあらあら不思議、なんと下のように、二つの画像が並んだ「平行法で眺める立体動画像」が作成されるのである。ちなみに、この立体化した動画像のreal形式動画像はこちら(perspective.rm 11kB )である。
 |
この交差法で眺める動画像を上手く立体視するコツは、遠くを眺めるようにして、ぼんやりと動画像を眺めてみれば良いだろう。そうすると、立体動画像で眺めるモンローウォーク(半裸)を眺めることができるハズだ。
ところで、先のこのソフトの立体化の原理を読んで、「いや、それだと動きによってはとても不自然になるに違いない」という人も数多くいることだろう。そんなアナタのその理屈は非常に正しい、と思う。しかし、まずは動画像を変換して自分の目で確かめてみてもらいたい。人間の感覚は時にとても簡単に騙されるのである。いや、あるいは人間の想像力の処理がスゴイのかもしれない。とにかく、本来不自然なはずの「立体動画像」も実際に眺めてみるとかなり自然な立体感を感じさせるのである。
というわけで、この原理の是非は次回以降に回すとして、まずはこのperspectiveを使って色々な動画像を立体化して眺めてみるべきと、私も色々な動画像を眺めてみたわけなのだけれど、試しに下のような「モーニング娘。」のライブビデオなんかも立体化してみた。
  |
で、この立体動画像を眺めながら、ちょっと私は考え込んでしまった。動画像中を走り回る「モーニング娘。」のメンバー達が手の届きそうな近くへ飛び出して見えたり、またあるいは、手の届かない遙か向こうの後ろにふと見えたりするのだ。それは確かに遠近感のある立体画像なのではあるが、ただの遠近感のある立体動画というわけだけでもないような気がしたのである。
何しろ、その走り回り、飛び出したりするメンバー達が今はもう実は「モーニング娘。」ではなかったりするのだ。何かそんなことを考えると、今眺めている動画像の奥行きが単に空間的な奥行きだけではなくて、何か時間的な奥行きを感じさせるような気がしたのである。時間的な距離を何か感じさせるような気がしたのである。
そう、そういえばこのperspective.exeが作る立体動画像は「時間的に前後に並んだ二つの画像を空間的に左右に並べて」みたものであった。つまりは、ビデオテープに記録された時間軸と空間軸をほんの少しばかりシャッフルすることで、遠近感を作り出しているのである。だから、perspective.exeが作る遠近感・奥行きは、実は「時間的な遠近感・奥行き」なのである。それを人間が勝手に「空間的な遠近感・奥行き」であるかのように錯覚していただけなのである。
だから、私がこの「モーニング娘。」の立体動画を眺めて、そしてもういなくなったメンバーなどを眺めて、何か時間的な奥行きを感じたりしても、それも実は結構正しかったりするのかもなぁ、なんて思ったのである。そんなことを考えながら辞書を引くと、遠近法を指す"perspective"は同時に「時間の向こう、見通し,展望,前途」なんてふうにも書いてあって、それを読みながら、ふ〜ん…としみじみ納得してみたりしたのである。
2002-02-18[n年前へ]
■「非線形処理+畳み込み処理」の公知資料 
特開2001-216513を出願した方からメールをもらった。「自然対数を使う数式自体は昔からあるとは思いますが、画像処理ソフトで、この計算を使ってピンボケを作り出すソフトまたはそのアルゴリズムが存在したのかご存じないでしょうか。」ということだった。
「非線形処理+畳み込み処理」はおそらく公知資料があるのではないか、ただし、非線形処理と畳み込み処理のいずれもが実装されたソフトは昔から多々あるが、それをワンアクションで実装したソフトは無いかもしれない、と返事を出した。また、「ところで、私自身は特許はあまり好きではないです。といっても、個人としてはですけど。それに、特許を申請するXXさんの考えも良く理解できます。」と書いた。で、メールの最後に
「それで、少し知りたいのですが、私は自分で作ったプラグインなどもいつもそうしているように何かの話のネタを作って、ソフト自体はフリーで配布すると思います。で、私以外にも自分で画像処理やプログラミングをしている人は多いので、そんなこともあるだろう、と思いますが、そういうときにXXさんはどうされるつもりでしょうか?」
と書いた。それへの返事は来ていないが、もう少し調べてみた。構成としては、特開平08-241407や特開平09-130609が近いか。で、昔に遡れば公知資料もあるかしらん。しかし、特許調査で公知資料探しなんてまるで仕事みたいでイヤだな。
SUB 画像ボケが「非線形変換→畳み込み→非線形」で表されるとの記述は昔の教科書に載ってた。SUB 特開平09-181966畳み込みでボケ味を出す、複数画像を撮影することで任意の距離のボケを実現。 by オリンパスSUB 特開平09-130609等LUT→ローパスフィルター→LUTで画像ボケ信号を作成 by 富士写真フィルムSUB 特開平07-200817フィルタリングによりボケ画像を作成する ダイキン工業SUB 特願平09-542474対数変換をした上で畳み込みを行う画像変換 サイエンスアンドテクノロジーSUB 特開平08-285726畳込みによるカメラなどの光学系シミュレーション ホーヤSUB 特開平08-241407非線形変換→畳み込み→非線形変換の画像変換 IBMSUB 特開2000-20691非線形変換+デコンボリューションによるぼけ復元、背景の説明中に、非線形変換+畳み込みによるボケ計算を説明 キヤノン
2002-02-21[n年前へ]
■今日のありがとうございます。 
なるほど、のご意見を頂いたのでここでもお礼を。
> ただ数学的に単に「定数だ」という主張はわからないでもない
> ですが、kという記号は普通はバネ定数力/距離に使います
> から、コンプライアンス距離/力に使われると少し違和感
> があります。例えば数式の中で周期にfという記号が使われて
> たら何となく嫌じゃありません?
あぁ、確かにそう言われればそうですね。そう言われると、
仰るとおり、何となくイヤですね。確かに、kというアルファベットを
使うのは良くないかもしれないですね。
あの式自体は、話の後半にkを「ヤング率」としてオチをつけたいので
年と比例しないとまずいので、力/距離は使えませんからアルファベットは
yとでも直してしておきます。
どうも、ありがとうございます。
ところで、「数学的に単に定数だという(乱暴な)主張」って理学部っぽく
ないですか?もちろん、人によりとても違いはありますが、
そんな私みたいな大雑把な理学部系って多くて、一方そんなことは
あまりない工学部系ってイメージがちょっと湧いたりしたのですが。