hirax.net::inside out::01月29日

■今日の景色　

　いたるところに雪だるま。良い感じ。（リンク）（リンク）

■Nothing but Echo　

　水面に映る「私たち」を書いた。書いていた時には気づかなかったことがたくさんあった。なんてことだろう。

■昼休みの「詮無きこと」　

　昼休みのホッケー仲間が一人減り二人減り、最近は寂しく楽しく三人でホッケーをしていた。だけど、その内のひとりが今週いっぱいで取手へ異動する。だから、来週からはきっと一人寂しく滑っているだけなんだと思う。冬の富士山はとても綺麗だけれど、だけど昼休みに一人で滑っているのはそれはとても寂しいなぁ、と思う。それはとても…、と思う。
　世の中には「詮無きこと」がたくさんあるのだなぁ、と今更ながらに気づいた。前は「詮無きこと」なんて口から出たこともなかったのに。

■11ぴきのネコ　

　演劇に興味を持ったのは、少し前。少し、と言ってもそれは二十年近く前のこと。春休み近くの高校で、演劇部が上演していた井上ひさしの「11ぴきのネコ」を見て、とても感動したのが演劇に興味を持つきっかけだったと思う。　いつも、合唱部やブラスバンド部の音楽に負けないくらい大きく、いつも屋上から「あめんぼ赤いな…」という声を響かせていた演劇部の上演会を観に行ったのだった。

北の空の大きな星あの星の下には幸せな場所がある

■今日見た写真　

　色の混じり具合が何とも素晴らしく感じる「美しい夕暮れ」こんな景色を見たら、何を考えるのでしょうね。(睦月便り camera full of kisses)

■本城直季・コンテナターミナル　

　実際の風景がミニチュア模型の写真にしか見えない「本城直季・コンテナターミナル」特徴は撮影角度と撮影画角の割に浅い被写界深度(に上か下をアオリでボカすことで見せかける)なのかな。あとは、色かなぁ？…けれどWEB経由の写真ではよくわからないか…。

■テレビクリップ　

負けた時に納得できる弁護士を選んで下さい。「法律」　橋下徹

■(16才の頃)「知っておきたかったこと」　

　Shiroさんが訳された「知っておきたかったこと」を読んだ。この文章を読んで引用した人と同じように、この文章の内容をできるだけ理解しようと、自分用にメモを取り直してみた。自分が話すなら…、と咀嚼し直さないとなかなかちゃんと読むことができないから、「もし講演が実現していたら…」と考えながら「本文6枚のPowerPointのファイル(PDF版-日本語訳全文はノートとして収録-, HTML, Flash版)」に適当に変えてみる。

　それにしても、16才の頃、同じ高校一年生として同じ高校へ通っていた、つまりは同窓生のShiroさんなどを見ると、「自分は二十年の間に何もできなかったなぁ」とつくづく思う。

人生の到達点はそれまでの積分なんだから、同じアドバイスがどの時点でも有効なはずだ。 やりたいことはたくさんある。それなら、絶対後悔しないから、貪欲に、遠慮せずにやればいい

■「理系タイプの彼を口説く方法」と「過去のオトコを語るバトン」　

　「“理系タイプの彼”を口説く方法」　「書き手もこんなことを信じて書いてるわけではないだろう」こういった記事は、「話のネタ・オツマミ」にして楽しむことができるのが、何より一番素晴らしい存在価値なのかもしれないと思う。「私の場合はこう思う」なんていう話を、井戸端会議のようにアレコレはなす事ができるという、「○×バトン」と同じシステムと同じように楽しめるのが流行る理由なのかもしれません。この記事をスタート地点にして、「これは違うだろう」「そういえばこうだった」…なんていう話を気楽にすることができるのが、こういった記事が広まる・読まれる理由に思えます。例えてみるならば、女性にとっては「過去や現在のオトコを語るバトン」、そして男にとっては、「オレ語りバトン」と言えるのかもしれません。

　「口説く方法シリーズ」は、その他にも“高学歴＆高収入エリート”“ルックス抜群！　ムリめな男前”“芸術肌オトコ”など色々あるようです。それだけあれば、色んな「過去や現在のオトコを語るバトン」ができそうですねぇ…。オトコにとっては…聞くのがツライ(だけど面白い？)バトンになるかもしれませんが…。

■「(16才の頃)知っておきたかったこと」と「11ぴきのネコ」　

　from n年前へ.　高校時代のことや高校時代に(同級生として)眺めた人を、ある年の今日思い出す。そして、その次の年の同じ日に、その同級生が訳した文章を読む。

それは二十年近く前のこと。演劇部の上演会を観に行ったのだった。

それにしても…、「自分は二十年の間に何もできなかったなぁ」とつくづく思う。

人生の到達点はそれまでの積分なんだから、同じアドバイスがどの時点でも有効なはずだ。

やりたいことはたくさんある。それなら、絶対後悔しないから、貪欲に、遠慮せずにやればいい。

■水面に映る「私たち」　

　3年前の今日、水面に映る「私たち」Nothing but Echoという文章を書きました。今日もまた繰り返される同じような「ニュース」を眺めながら、私はふとこの文章を思い出します。もしも、このページに訪れた「あなた」に少しの時間があるのなら、この文章を読んで頂ければ、少し嬉しく思います。
　「水面を上から覗きこんでみれば、その水面に景色だけでなく私たちの姿も同時に映りこんでいるように、ギリシャ神話のナルキッソスが泉の中に自分自身の姿を見たように、その『ニュース』には世の中の出来事だけでなく、私たち自身だって写りこんでいるに違いない」という言葉の先にあるものを、かすかに眺めて頂くことができたなら、私はとても嬉しく思います。3年と少し前に、テレビで流されていた「問いの答え "YES""NO"」をあなたに眺めてみてもらえたら、と思っています。

その問いの中の、そして、その答えの中の「テレビニュース」の部分は全て「僕ら自身」と置き換えられるのだから…

「私たち」が世の中に与える影響は？ 「私たち」は信用できる？ 「私たち」はあなたの人生にとって 「なくてはならないもの」ですか？

■若者ライフスタイル分析　

　「私たちが描いている若者たちのイメージは、果たして現実をとらえているのか？」という、TOKYO FMが1995年度から実施している「若者ライフスタイル分析」　どんなメディアを眺めて、どんなコミュニケーションをして、どんな生活を…と、色んな面に対する調査結果を眺めてみると、とても新鮮で興味深い。
　そして、ほんの数年前の調査設問や結果を眺めてみるのも、時の流れが見えて、面白いと思う。

■"We have learned to live with this stupidity"　

　1925年に生まれた 菊池誠が1990年に書いたのが「若きエンジニアへの手紙」（ダイヤモンド社）だ。65才になった半導体研究者の著者が、若きエンジニアに対し、真摯に優しく語りかけるように言葉を重ねた本だ。時が過ぎて、企業の中央研究所や大学の姿が変わっていったことを考えれば、この「エンジニア」という言葉は、今では、もう少し「研究者」寄りととらえた方が良いかもしれない。

　この本はとても良かった。「若きエンジニア」という部分で、手に取ることをためらう中年エンジニアや研究者もいるかもしれないけれど、65才になった優れた著者が言う「若き」なのだから、どんな年齢でも、恥らわずに手にとって読んでみるといいような気がする。

　たくさんの文章をメモしたけれど、20ページ目にある「トランジスタの父」ショックレーの論文の一部をここに書き写そう。

“What I say about myself-and I am sure most creative people would say the same thing is that, when we look at how long it took us to get certain ideas, we are impressed with how dumb we were- on how long it took us, and how stupid we were. But We have learned to live with this stupidity, and to find from it what relationships we should have seen in the first place. This recongnition that we aren't perfect but that persistence pays is a very important factor, I think, in giving one the "will to think"-you don't need to worry so much about the mistakes you make.

■「数字で語る」と「プロフェッショナル」　

　中谷巌 「入門マクロ経済学 第三版」を読んでいるとき、「内容を理解・使うことができるようになっているか、それとも、そうでないかが、数字の収支を眺めてみると、あるいは違う例を用いて頭の中で考えてみると、自動的に明らかになってしまう。

　だから、この本をとても本当の意味で「なんて理解しやすいんだろう」と感じたとき、ふと「今井功の「当然！」「○」「？」」を思い出した。

「わからないこと」を無理してわかろうとしない方が良いんだ「わからないこと」というのはたいていどこかおかしい。

今井功

数値で語れなければ、プロとは言えない。

今井功

■本当の私はもっと「キレイ」!? 　（初出：2005年09月01日）　

　「心の中が見える装置」ではありませんが、普通は見ることができないものを、実際に自分の目で眺めてみるというのは、とても面白いものです。

　「人が一番見ることができないもの」とは、一体どんなものでしょう？・・・もしかしたら、「人が一番見ることができないもの」の一つが、「他人が眺める自分の顔」かもしれません。

　自分が眺める「心の中の自分の顔」と、他人が実際に眺めた「客観的な自分の顔」は結構違うことが多い、と思ったことがある人は多いのではないでしょうか。

　デジカメで撮影された自分の顔を眺めて、「本当の自分の顔はこんなじゃないのに…私は写真写りが悪いの？」なんて考えたことがある人もいるのと思います。

　そういえば、人の顔写真を「何が何でも美人にしてしまう」美人フィルタというものを作ったことがあります。どんな顔でも？「お目々パッチリの美人顔」にしてしまうソフトです。

　顔写真を撮って「撮影した顔」と「美人化した顔」を見せられたら、人は「美人化した顔」の方が「本当の自分の素顔」だと、主張する・思うのではないだろうかと、ソフトを作った時にふと考えました。

　他人＝周りの人は当然のことながら、「撮影した（誰かの）そのままの顔」を「本当の顔」だと思うことでしょう。けれど、その一方で、撮影された本人からすれば、「撮影した顔」では、「本当の顔をちょっとブサイク化」したものに思えてしまうのではないか、と予想したのです。「美人化した顔」の方こそ「本当の自分」だと感じているのではないか、などと妄想したのです。

　「人が一番見えないものは、自分自身だ」といいます。美人かした写真・そのままの写真・ブサイク化した写真、・・・そのうちの一体どれを、人は自分自身だと思うのでしょうか？

■歯医者さんの「うがい用カップ注水器」のナゾ　

　歯医者さんに行くと、いつも「うがい用のカップ」に水を注ぐ機械が気になります。紙コップを置くと、うがいをするための水や液体を自動で注ぎ始め、ちょうどよいくらいの高さまでくると（これまた）自動でストップするという機械です。

　昔は、コップを置く部分にスイッチが設置されていたこともあるような気もしますが、今ではそのような機械を見ることはなくなってしまいました。そこで、自動注水機構がどのように動いているのかを知りたくて、椅子に座って治療を待ちながら、コップに水を注ぐ部分を下から眺めてみました。すると、そこには穴が３つ空いていました。

　もちろん、その穴の内のひとつは、注水口に違いありません。ということは、残り２つで水の量を計測しているのだろう、ということになります。ふたつの穴ということは、片方は”何かを出す”穴で、もう片方が”何かを受ける穴”という具合に思えます。

　となると、まず思いつくのは光を水面に対して斜めに照射して、水の量が所定の高さになった時の水面からの鏡面光を受ける位置に光を受けるセンサを配置する、というやり方でしょうか。あるいは、超音波を出して、その反射を受けることで距離を測るというやり方でしょうか。

　歯医者さんの行くのが好き、という人はほとんどいないでしょうが、そこにある「うがい用カップ注水器」を眺め、その仕組みに心惹かれてきた人は多いのではないでしょうか。あの歯医者さんの「うがい用カップ注水器」は一体どんな仕組みになっているのでしょうか？

■「Mathematicaの色（スペクトル計算）関数」手直し版　

　Mathematicaで色（スペクトル）計算をしたり、計算結果を表示するのに便利な関数を（ほんの少しだけ）作り直しました（ColorImagingFunctions.txt）。CMYKの画像ファイルを開き、「画像のこの辺りのピクセルは、一体どんな色（スペクトル）になるんだろう？」なんていう計算をする時の「叩き台」になるかもしれない（ならないかもしれない）という、そんな関数群です。

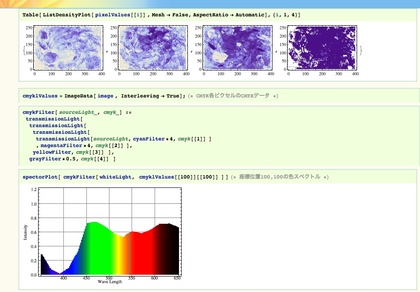
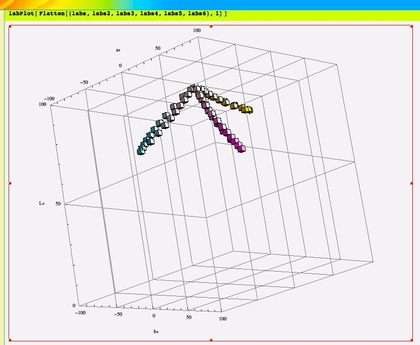　たとえば、右に貼り付けた画像は「典型的なカラーインクの吸収スペクトル（シアン・マゼンタ・イエロー）で面積階調・濃度階調を表現した際の色変化を示したグラフです。こういった処理を下記のようなコードを書くことで行うことができる、そんな関数群を書き直してみました。

labs = Map[lab, 
  Table[transmissionLight[D65, 
   cyanFilter, d], {d, 0, 4, 0.4}]]
labPlot[ labs ]

■Wolfram Alphaに「ブラジャー」検索をかけてみる!?　

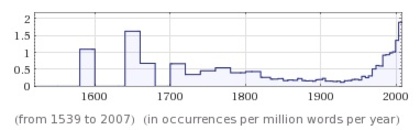　Wolfram Researchが提供する知識（データベース）エンジンであるWolfram Alphaに「ブラジャー（bra）」という言葉で検索をかけてみました。すると、20世紀半ばから"bra"という言葉が使われることが増えてきたということがわかったり、あるいは、"平均ブラサイズ（average bra）" という検索をかけてみると、アメリカでは（研究報告によって異なるけれど）３６インチCカップくらいで、ヨーロッパでは３４インチCカップくらいらしい、ということがわかります。

　ちなみに、Wolfram Research の数式処理ソフト MathematicaはWolfram Alphaからデータを取得することができます。たとえば、右上の「ブラの言葉頻出度」は次のようなコードで取得することができます。 Mathematica

WolframAlpha["bra", "PodCells"][[7]]

WolframAlpha["bra", "PodCells"][[5]]

　昔のこどもたちは、国語辞書や英語辞書で「エッチ」な言葉を繰り返しひいたものでした。２１世紀もはや十数年、辞書の種類は変わっても、今のこどもたちも各種知識計算エンジンにエッチなキーワード検索をかけていたりするのでしょうか？

■「手持ちスマホ撮影動画からの超巨大開口レンズ撮影」に挑戦してみよう!?　

　かつて、スマホに搭載されているカメラのレンズはとても小さく、綺麗なボケとは無縁の存在でした。しかし、今や最新のスマホには特殊処理によるボケ生成機能などが備えられています。カメラレンズの光学開口径が小さくとも、たとえば２眼カメラなどを備えて距離情報を取得して、距離情報などからボケを人工的に合成するといった仕組みです。

　そんな最新スマホを持たずとも、大レンズのボケ味を手に入れるために、「手持ちスマホ撮影動画からの超巨大開口レンズ撮影」に挑戦してみました。スマホ動画から巨大開口レンズ撮影の手順はとても簡単、まずは目の前の風景にスマホを向けて・なるべくスマホが平面上を動くように意識しながら（スマホを動かしつつ）動画撮影します。そして、動画の各コマから画像ファイル群を生成し、それぞれの画像が撮影された位置や方向にもとづいて撮影された光情報を加算合成する、というものになります。

　細かい手順は、スマホ撮影動画（の展開画像をもとに） Bundler: Structure from Motion (SfM) から出力された刻々のカメラ位置・方向や特徴点情報ファイル(bundler.out)を読み込み、それらのカメラ情報にもとづいて、刻々の撮影画像をレンズ開口面に沿った（同じ方向を向く平行カメラが存在していた場合の）光線画像を位置・角度ズレを踏まえて重ねることで、任意のピント位置に焦点を合わせた超巨大開口レンズ撮影画像を生成する…というものです。

　試しに、iPhoneを約1.5m×1.0mの範囲で動かしつつ動画撮影し、つまり、レンズ直径約1.5ｍに相当する範囲で動かしつつ動画撮影し、その画像群から開口合成により超巨大カメラの撮影画像を作り出してみた結果が右上の画像です。

　ちなみに、試しに各画像を（撮影方向による傾きを補正しつつ）位置毎に並べてみると、下の画像のようになります。動画撮影からのカメラ位置推定精度が果たして不十分なのかどうか、次は撮影カメラ位置を精度良く知る事ができる撮影治具でも作り、また再挑戦してみたいと思います。

　上記処理のコード手順、Python/OpenCVで書いたコード処理手順は、bundler.outからカメラ位置・方向・焦点距離や歪みパラメータを読み込み、cv2.initUndistortRectifyMapにカメラ情報を渡して、各撮影画像の向き補正用のホモグラフィーマップを作成してremapで変換した後に、各撮影画像を加算合成するという手順です。

　Bundlerの出力ファイルを読み込んでライトフィールド合成を行うOpenCV/Pythonコード、まだまだ間違い含まれているような気もしますが、とりあえずここに貼り付けておくことにします。

import cv2
import numpy as np
from matplotlib import pyplot as plt
from PIL import Image
import math
%matplotlib inline

class camera:
    def __init__(self):
        self.f = 1.0
        self.k1 = 0.0
        self.k2 = 0.0
        self.R = [[0.0,0.0,0.0],[0.0,0.0,0.0],[0.0,0.0,0.0]]
        self.T = [0.0,0.0,0.0]

def readBundlerOut( filePath ):
    f = open(filePath, 'r')
    list = f.readlines()
    f.close()

    numberOfCameras = int((list[1].split())[0]) 
    cameras = []
    for i in range(numberOfCameras):
        aCamera = camera()
        fk1k2 = [float(j) for j in list[5*i+2].split()]
        aCamera.f  = fk1k2[0]
        aCamera.k1 = fk1k2[1]
        aCamera.k2 = fk1k2[2]
        rot = []
        for j in range(1,4):
            rot.append( [float(k) for k in list[ 5*i+2+j ].split()] )
        aCamera.R = rot
        aCamera.T = [float(k) for k in list[ 5*i+2+4 ].split()]
        cameras.append(aCamera)
    return cameras

def readImageList( listPath, imageDirPath ):
    f = open(listPath, 'r')
    list = f.readlines()
    list = [ i.rstrip() for i in list ]
    f.close()
    list = [imageDirPath+fileName for fileName in list]
    return list

class lightField:
    
    def __init__(self):
        self.w = 2000
        self.h = 2000
    
    def loadImageListAndMakeLightField( self, 
                    imagePathList, cameraList, workList, scaleA ):
        self.cimg  = np.zeros((self.h, self.w,3), dtype=np.uint8)
        sum = 1.0
        for i in workList:
            img = cv2.imread( imagePathList[i], cv2.IMREAD_COLOR )
            h, w = img.shape[:2]
            imageHeight = img.shape[0]
            imageWidth =  img.shape[1]
            focalLength = cameraList[i].f
            principalPointX = 0.500000
            principalPointY = 0.500000
            distCoef = np.array([ 0.0, 0.0, 0.0, 0.0, 0.0 ])
            cameraMatrix = np.array([ 
                [focalLength,   
                 0.0,          
                 imageWidth  * principalPointX], 
                [0.0,           
                 focalLength,  
                 imageHeight * principalPointY], 
                [0.0,           0.0,          1.0] 
                           ])
            newCameraMatrix, roi = cv2.getOptimalNewCameraMatrix(
                cameraMatrix,
                distCoef,
                (img.shape[1], img.shape[0]),1,
                (img.shape[1], img.shape[0]) )
            rotMatrix = np.array( cameraList[i].R )
            map = cv2.initUndistortRectifyMap( 
                newCameraMatrix,
                distCoef,
                rotMatrix,
                newCameraMatrix, 
                (img.shape[1], img.shape[0]),
                cv2.CV_32FC1)
            
            undistortedAndRotatedImg = cv2.remap( img, 
                        map[0], map[1],
                        cv2.INTER_LINEAR )
            
            scale = 1.0
            pt3 = np.array(cameraList[i].T) - np.array(cameraList[0].T)
            x =  ( self.w/2.0 - pt3[0] * scale * scaleA ) 
            y =  ( self.h/2.0 - pt3[1] * scale * scaleA ) 
            pts1 = np.float32( [[0,      0],
                                [w, 0],
                                [w, h],
                                [0, h]])
            pts2 = np.float32(  [[x,           y],
                                 [x + w*scale, y],
                                 [x + w*scale, y + h*scale],
                                 [x,           y + h*scale]] )
            M = cv2.getPerspectiveTransform( pts1, pts2 )
            img2 = cv2.warpPerspective( 
                undistortedAndRotatedImg, M, (self.w, self.h) )
            sum = sum + 1.0
            self.cimg = cv2.addWeighted(
                 self.cimg, (sum-1) / sum, 
                 img2,      (1.0) / sum, 0)
    
    def showImage(self):
        plt.figure( figsize=(14,14) )
        plt.imshow( np.array(self.cimg2) ) 
        plt.autoscale( False )