2001-08-07[n年前へ]
■「ボケ」た背景で包み込め 
デジカメ画像をキレイにボカそう アルゴリズム編
最近、新しいデジカメを物色中である。私はこれまではFinePix4700zを使っていたのだけど、そのFinePixが半年程度で壊れてしまった。というわけで、C-4040ZOOMがどんなものか期待しているところである。
壊れたFinePixと言えば、そもそも壊れたFinePixは一台ではなかった。私はすでにFinePixを二台も買っているのだ。そして、もうすでに二台とも壊れてしまっているのである。連続殺人事件ならぬ、連続カメラ自殺事件なのである。
まず、一台目に買ったFinePix700ははメキシコのティファナでポケットから落としたら、バッテリーから電源が供給されなくなった。もちろん、ACアダプターを使えば立派に動くのだけれど、それでは少しばかり機動性に欠けてしまう。まさか発電機を持ち歩くわけにはいかないし、コンセントの近くでしか撮影することができないとなると、それは非常に困ってしまう。そこで、すかさず二代目としてFinePix4700zを私は買った。ところが、買ってから半年位たったある日、今度は勤務先の駐車場でポケットから落としてしまった。すると、今度はファインダー視野がズームに連動しなくなって、なおかつレンズがまるでジョイスティックのようにあらゆる方向に曲がるようになってしまった。
こんな風にデジカメはとっても壊れやすくて、半年毎にデジカメ出費を強いられる私に周囲は「落としたオマエが悪い」と非常に冷たいのである。残念なのだ。「そういうのは壊れたんじゃなくて、壊したんだ」と被害者である私をまるで加害者のように告発する人さえいるのである。連続カメラ自殺事件は実は他殺で、しかも犯人は私だと告発する輩さえいるのだ。ひどい話である。
ところで、C-4040に期待しているのは、コンパクトで、レンズアダプターが使えて、レンズがF1.8と明るいことなのである。コンパクトなのは持ち歩くために必要だし、私はなんと言っても超広角デジカメが欲しいのだが、そんなデジカメはないので、ワイドコンバーターを付けたいのでレンズアダプターが必要なのである。明るいレンズの方は、うす暗い中でも撮影する時に重宝しそうなので、少し期待しているのである。
ところで、この位明るいレンズであれば、もう少しぼかすことができるものだろうか?デジカメで写真を撮ってもどうしてもボケない。35mmフィルムを使っているカメラなどと比べるともう全然ボケない。もうほんとにボケない。
例えば、35mmカメラで135mm F4.5開放のレンズなら、ピントの合ってない背景はこの位はボケる。これは京都の哲学の道近くにある吉田山で撮った写真だ。
 |  |
ピントが合っている位置以外は光がボケて、キレイなボケが発生する。どちらの写真も絞りは開放で撮影しているので、後ろの風景はほぼ丸くボケている。ぼかせばキレイというわけではないけれど、背景などがごちゃごちゃしている中で対象物だけを浮き上がらせたい場合には、「ボケ」させるととても良い感じになる。
しかし、デジカメではそうそう簡単にボケた画像を撮影することはできない。35mmフィルムに比べて、CCDサイズが小さいからである。35mmカメラよりAPSカメラはもっとぼけなくて、それよりデジカメはさらにボケないのである。そんな様子を見るために、二台目として買ったFinePix4700zで「ボケ」を意識して撮影してみたものが下の写真である。手前の植物にピントが合って、奥の道の先はボケてはいるのだけれど、それでも先程の写真などとは比べものにならないほどわずかしかボケていない。
 |
ところで、このような画像の「ボケ」を考えるとき、「ボケ」た画像をシャープに復元しようという話は非常にポピュラーな話題である。例えば、本「できるかな?」でもこれまでに
といった感じで遊んできた。また、さらには「恋の形」を復元しようとしたとか、このようなアプローチを遥か昔に考えていた漱石の「文学論」を振り返ってみたりしたきたのである。しかし、これらはいずれも「ボケたデータを復元する」という問題であった。一方、この逆のアプローチである「シャープなデータをボケたデータにする」という問題も結構ポピュラーである。例えば、音楽をホールやライブハウス風にボケた音にするDSPはかなりの数のオーディオ装置に付けられている。これも、もともとはシャープな音声データが部屋の中でボケていく様子をシミュレートする回路である。また、画像に関する話題でも、ピント位置をずらした複数の画像から任意の「ボケ」画像を作成するといった話題もたまに見かける。
そこで、「できるかな?」でもデジカメ画像を35mmカメラ風にキレイにぼかすことに挑戦してみることにした。今回は、まずはアルゴリズムを確認して、次回以降で簡単プログラムを作成してみることにしたい。
まずは、似たようなソフトウェアがあるかどうか、Googleで適当なキーワードを使って検索をかけてみると、IrisFilter(http://www.reiji.net/iris/)というソフトウェアがあった。これは、「写真のぴんぼけを再現する」というフィルターだった。サンプル写真などを見てみると、これがなかなかきれいだった。例えば、早朝の御殿場の路上を「在りし日のFinePix4700z」で撮影した写真にこのフィルタをかけて、「ボケ」を加えてみたのが下の画像である。
 |  |
ここではこんな![]() 六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
WEBページの記載によれば、このIris Filterは「フィルム特性曲線を利用し、レンズから通った光がフィルムを感光させる様子を再現しています」ということである。なんでも、特許も国内・USP共に出願済みということだが、特願2000-100042もU.S.PTO 09/772532も未だ公開にはなっていないようで、残念ながら特許の内容を読むことはできなない。
このWEBページの記述の中で面白いのは、「データ上の数値をそのまま拡散させる従来のPhotoshopをはじめとした画像処理ソフトと違い、実際のフィルムに当たる光の量(露光量)を逆算し、その露光量をもってピントがずれている様子を再現します」という歌い文句でPhotoshopの「ガウスぼかし」と比較広告してある部分である。
試しに、先の画像をIris Filterで「ボケ」を加えた画像と、Photoshopの「ガウスぼかし」とで「ボケ」を加えた画像を比較してみると、下の二枚の画像のようになる。確かにIrisFilterの売り文句通り、こうして比較してみるとPhotoshopガウスぼかしが写真の「ボケ」っぽくないのに対して、IrisFilterの「ボケ」が写真のそれっぽいことが良くわかる。
 |  |
さて、お仕着せのソフトを使ってみるだけではなくて、自分でデジカメ画像をキレイに「ボケ」させてみることにしたい。というわけで、hirax.net風「ボケ」フィルターの動作を考えてみる。
まずは、毎度のことだがオリジナル画像が「ボケ」る様子を計算する式は
逆フーリエ変換( フーリエ変換( オリジナル画像 ) x フーリエ変換(ボケ具合 ) )と表すことができる。詳しくは、「宇宙人はどこにいる?」の回でも読んでもらうことにして、簡単に言えば周波数領域でオリジナル画像とボケ具合を掛け算をしさえすれば良いのである。つまり、今回のデジカメ画像をぼかす場合だったら、
- デジカメ画像と「ボケ」具合をそれぞれフーリエ変換し周波数空間に変換
- 周波数空間で乗算を行う
- 逆フーリエ変換して実空間に戻す
じゃぁ、早速やってみようとなるわけだが、その前にもう一つ注意することがある。それは、RGB画像の数値というものは実は元々「明るさを対数変換した値」であるということなのである。人間の目も含めて世の中の大抵の材料は対数的な感度を持っている。例えば、人間の目に「2倍明るい」という場合に、光は「2倍明るい」というわけではない。その場合には指数的にX^2倍明るいのである(ここで、xの値はそれぞれのデバイスによって色々と違う)。その明るさをRGB画像の数値データにする時に、明るさの対数をとってLog[x,X^2]で2という数値として表しているわけだ。
RGB画像の数値が「明るさを対数変換した値」だというようすの一例を示すと下の図のようになる。
横軸 = 0〜255の数値データ 縦軸 = エネルギー  | 横軸 = 0〜255の数値データ 縦軸 = エネルギー  |
逆に明るさからRGB画像の数値データへの変換グラフは例えばこんな感じである。RGB数値で200と255と言っても実はその明るさは大違いであることがわかると思う。
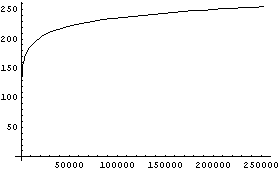 |
だから、この手の処理を行う際には、まずは指数変換してから処理を行い、そしてその後対数変換してやらなければならないわけだ。もちろん、今回のデジカメ画像をぼかす場合にも、RGB画像の数値をまずは指数変換した後、「ボケ」演算を行って、その演算結果を対数変換でRGB画像の数値に戻してやらなければならないのである。といっても、別に難しい話ではなくて画像を扱う装置だとごく当り前の話だ。
そう、「ボケ」演算のhirax.net風レシピはたったこれだけ〜というわけで、早速このレシピに従ってhirax.net風デジカメ「ボケ」フィルターをかけてみたのが下の画像である。キレイな「ボケ」画像ができあがっていることが判ると思う。
 |
ところで、デジカメ画像のRGB画像の数値を指数変換したものに「ボケ」演算を行ったわけだけれど、もしRGB画像の数値そのものに対して「ボケ」演算を行ったら、どんな結果になるだろうか?つまり、「データ上の数値をそのまま拡散させる」やり方をしたら、どうなるのだろうか?そこで、試しにRGB画像の数値そのものに対して「ボケ」演算を行ってみるとこんな結果になる。
 |
何だかボンヤリとにじんだだけの「キレイじゃない」写真になってしまっている。それは、当り前である。本来2倍明るいものはX^2倍明るいわけで、すごく光の量は2倍どころでなく多いわけだ。それが広がる量を仮にRGB数値そのまま2倍として扱ってしまうと、その光の部分は薄暗くなってしまう。コントラストのはっきりしない、ぼんやりとした写真になってしまうわけだ。ちゃんと、X^2倍のデータとして扱ってやらなければならないわけである。
試しに、指数処理したものと線形処理をしたものとを並べてみるとその画像の違いがよくわかるだろう。
キレイなボケ画像(指数処理)  | キレイじゃないボケ画像(線形処理)  |
さて、今回はデジカメ画像の「ボケ」フィルターのhirax.net風レシピを確認してみた。次回(と言ってもいつになるか…)以降に、このレシピに従って実際にソフトを作成していこうと思う。
ところで、「文学論」の中で漱石は「ボケ」は焦点的印象又は観念に付随する情緒を意味する、と言っている。それは、言い換えれば「何かの出来事をきっかけとして感じた怒り・悲しみ・喜びなどの感情がボケである」ということだ。そして、さらに言えば、写真で背景をぼかすということは、つまり「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて包み込む」ということなのである。
だから、何かを撮影する時に対象物の背景をぼかすということは、「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて対象物を包み込んで、そして対象物を浮き上がらせる」ということなのかなぁ、とぼんやりと考えてみたりする。そんな写真は対象物を写しこんでいるのと同時に、それを包みこむ背景も写しこんでいるンだろうなぁ、と考えてみたりする。

2001-12-24[n年前へ]
■サンタが街にやってくる 
複数サンタクロースの巡回問題
簡易に書き直した2011年版もあります。
幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで(高原の診療所なのだから大して違いはないのだけれど)、とても不思議だった。
さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。
知らない人のために書いておくと、「巡回サンタクロース問題(TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが
- サンタクロース研究
- ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )
そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。
まず、始めに問題提起をしてみよう。
「果たしてサンタは一人なのか?」
どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。
そこで、まずはサンタの歴史から調べてみると、Santaさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。
とはいえ、Santaさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか?
また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
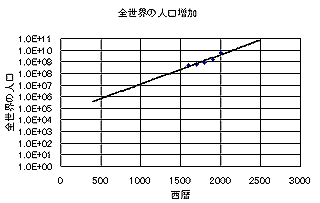 |
St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。
サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。
子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 |
どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。
先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。
そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。
それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
一例として、サンタが1,2,10人の場合を示してみる。
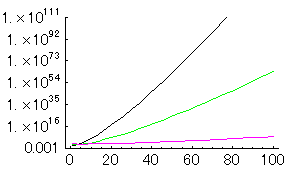 |
このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。
実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。
このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。
ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。
それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。
ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。
もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。
こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。
サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。
2002-02-18[n年前へ]
■「非線形処理+畳み込み処理」の公知資料 
特開2001-216513を出願した方からメールをもらった。「自然対数を使う数式自体は昔からあるとは思いますが、画像処理ソフトで、この計算を使ってピンボケを作り出すソフトまたはそのアルゴリズムが存在したのかご存じないでしょうか。」ということだった。
「非線形処理+畳み込み処理」はおそらく公知資料があるのではないか、ただし、非線形処理と畳み込み処理のいずれもが実装されたソフトは昔から多々あるが、それをワンアクションで実装したソフトは無いかもしれない、と返事を出した。また、「ところで、私自身は特許はあまり好きではないです。といっても、個人としてはですけど。それに、特許を申請するXXさんの考えも良く理解できます。」と書いた。で、メールの最後に
「それで、少し知りたいのですが、私は自分で作ったプラグインなどもいつもそうしているように何かの話のネタを作って、ソフト自体はフリーで配布すると思います。で、私以外にも自分で画像処理やプログラミングをしている人は多いので、そんなこともあるだろう、と思いますが、そういうときにXXさんはどうされるつもりでしょうか?」
と書いた。それへの返事は来ていないが、もう少し調べてみた。構成としては、特開平08-241407や特開平09-130609が近いか。で、昔に遡れば公知資料もあるかしらん。しかし、特許調査で公知資料探しなんてまるで仕事みたいでイヤだな。
SUB 画像ボケが「非線形変換→畳み込み→非線形」で表されるとの記述は昔の教科書に載ってた。SUB 特開平09-181966畳み込みでボケ味を出す、複数画像を撮影することで任意の距離のボケを実現。 by オリンパスSUB 特開平09-130609等LUT→ローパスフィルター→LUTで画像ボケ信号を作成 by 富士写真フィルムSUB 特開平07-200817フィルタリングによりボケ画像を作成する ダイキン工業SUB 特願平09-542474対数変換をした上で畳み込みを行う画像変換 サイエンスアンドテクノロジーSUB 特開平08-285726畳込みによるカメラなどの光学系シミュレーション ホーヤSUB 特開平08-241407非線形変換→畳み込み→非線形変換の画像変換 IBMSUB 特開2000-20691非線形変換+デコンボリューションによるぼけ復元、背景の説明中に、非線形変換+畳み込みによるボケ計算を説明 キヤノン
2002-06-07[n年前へ]
■ある種類のアート 
先日、NTTインターコミュニケーションセンターに行った。正直に言えば、とてもつまらなかった。スペースの縮小のせいか、展示されていたのは三人のアーチスト分の展示だけだったが、その内の二人は非常に安易でつまらなかった。もう一人(井上尚子だったか?)は安易ではあったが、その三人の中ではまぁ面白かった。
が、これは私の趣味での話で、他の人なら当然違うだろう。だからこそ、スペースの縮小に伴う、展示数の激減はとてもツライと思う。自分の趣味に合う展示の絶対数が激減するからだ。
で、私の手元にはNTTiccと似た存在であって、そしてこちらも同じくほぼ消えたキヤノンアートラボが出していた技術報告のバインダーがある。とても、面白い内容でうらやましいのである。(リンク)(リンク)(リンク)
2002-08-04[n年前へ]
■キラキラ光る景色を描く 
「木漏れ日」プラグイン「リン」を作る
夏の休日には、朝早く起きて西伊豆の松崎の先にある「雲見・岩地・石部」辺りへ行って、海の中でお魚と戯れてみたり、海辺の温泉に長々とつかってみたりする。例え休日であっても朝早く行けば混雑とは無縁だし、海に照りつける太陽と温泉とビールの三点セットが揃えば、夏の景色としてはとても素敵なのである。
とはいえ、今日は朝寝坊したので、松崎までは行かずに「無名だけれどとても良い感じの場所」へ行った。海辺に車を止めて、景色を眺めて、ほんの少しの時間泳いでみた。下はその西伊豆の某所で眺めた「今日見た景色」だ。
 「雲見、岩地、石部」であれば温泉も海も最高だけれど、西伊豆の辺りには他にも「海水が綺麗で、人も全然いなくて、トイレも水もある」ような場所はいくつもある。これはそんな場所の一つ。 県道から海辺の集落に向かう道沿いには素晴らしい滝もあって、まるでプレイステーション2のゲームソフト「ぼくのなつやすみ2海の冒険篇」の世界に迷い込んだかのよう。 実際に眺めていた景色はもっとキラキラしていたハズなのに、その片鱗も残っていない…。それはひとえに写真を撮ったワタシのウデが悪いから。 |
海辺でワタシが実際に眺めていた景色は、もっとずっと「キラキラ」していたハズなのに、残念なことに上の写真を眺めてみても、その片鱗すら残っていない。揺れてる波間も、足下の濡れている岩も、眩しい太陽だってもっとずっとキラキラしていたハズなのに、上の写真はただボンヤリした写真になってしまっている。それは、ひとえに写真を撮ったワタシのウデが悪いからである。もちろん、それが一番の理由である。クヤシイ話ではあるが、確かにワタシのウデは悪いのである。
とはいえ、言い訳を少しばかり書くならば、実際に眺めていた景色がもっとずっとキラキラしていた理由は他にも考えられる。例えば、ワタシ達が景色を眺めるときには、目の前にかかる髪の毛や、睫毛や、目の水晶体を通して景色を眺めているわけで、それらの中で光が回折したりして、キラキラとまるで虹のように光が輝いて見えたりするからだ。そのため、例えば夜空の星の形、本来は丸いはずの星の形、が星型に見えたり、木漏れ日が虹のように輝いて見えたりする。
そんな様子をもしカメラで再現しようとするならば、ケンコーが出しているクロスフィルターのようなものをつけることになる。しかし、手軽さが取り柄のデジタルカメラでわざわざそんなフィルターをつけるのは面倒くさいし、第一人によって見え方は違うから、「ただ一つのフィルター」で写真を撮ってしまうのは少しばかりイヤな気がする。例えば、「私は目の前に髪の毛がたくさんかかってしまって邪魔なのー」という人もいれば、「最近、抜け毛がハゲしーなぁ…、目の前に髪の毛がたくさんかかっていたあの頃が懐かしぃ…」という人もいるわけで、そんな二人が眺めた景色はきっと全然違うハズなのである。「百人の人がいれば百人百葉様の景色を眺めている」わけで、写真を撮る時点でただ一つのフィルターをデジカメにはめて写真を撮ってしまうのも面白くない。フィルターに限らず、何事も一つの枠にはめてしまうのは良くないのである。
デジカメの便利なところは、何より撮った後の画像加工が自由自在、というところなわけで、撮った後に「眺めた景色」を再現するように画像を加工してやれば、「写真を撮るときには素直な景色を撮って」「その後で自分が眺めたキラキラ光る景色を蘇らせる」ということができる。そこで、今回はそんな「キラキラ光る景色を描く」Photoshop用のプラグインを作ってみることにした。そして、ワタシの写真の腕の悪さを「技術の力」で誤魔化そうと思うのである。
といっても、基本的には、「ボケ」た背景で包み込めの時の処理を基にして、
- 色々な畳み込みの演算カーネル形状を用意し
- 演算カーネルのサイズを強度やアルファチャンネルの情報を元にしてピクセル単位で可変にし
- カーネル演算を対数変換有無などに対応する
RINgの出力サンプルを少し眺めてみると、下の画像のようになる。まず最初のサンプル画像は、クローバーの写真に「虹十字状」の畳み込みの演算カーネルを用いて、処理をしてみたものだ。左のオリジナル画像では、朝露を載せて光るクローバーを眺めるときに私達が感じる「キラキラしたようす」がほとんど写っていないが、右のフィルター後の写真では私達が睫毛などを通して景色を見るときに感じる虹色のキラキラした自然?な景色が映し出されている。
| (畳み込みの演算カーネルは虹十字状)  |
そして、また下の写真は、新宿から初台へ歩く途中で眺めた木漏れ日の向こうのビルの景色だ。左のオリジナル写真はクッキリ・ハッキリ写っているのだが、ただ「それだけ」である。太陽の光を遮る木々の葉っぱも、そこから降り注ぐキラキラする木漏れ日も写ってはいない。しかし、右のRINgが描いた景色の方では、ボンヤリと、だけど強く光る初夏の「木漏れ日」が確かに写っているのである。夏の空気が写っているかのようなのだ。
| (畳み込みの演算カーネルは円状)  |
もちろん、このRINgは「ボケ」た背景で包み込めの時の処理を基にしているので、写真のボケも再現することができる。例えば、六角形の畳み込みの演算カーネルを用いて、画面全体に同じ演算カーネルで処理をかけると下の右の写真のようにピンボケの写真を再現することができる。
 |  |
また、アルファチャンネルも選択してフィルタ処理を行うと、自動的にアルファチャンネルの情報を基に畳み込みの演算カーネルサイズを画素毎に変化させる。だから、例えばアルファチャンネルに距離の情報を入れておいてやれば、下の写真のように距離に応じたボケなども再現することができる。この写真では画面中央下の領域はピントが合ってていて、そこから離れるに従って、ピンボケの具合が大きくなっている。もっとも、現在のバージョンでは大雑把に計算してみただけなので、空の部分などに疑似輪郭などがずいぶんと発生してしまっている。きっと、それはいつかのバージョンで直すつもりなのである。
 | (畳み込みの演算カーネルは円状)  |
今回のRINgプラグインは光が広がる様子を保存した「畳み込みの演算カーネル」を基に画像にフィルタをかけるだけなので、使う演算カーネルの形状・様子によって色んなフィルタに早変わりする。
例えば、デフォルトでつけてある三日月型の"Moon"カーネルを使えば、色んな灯りが三日月型に光る景色に早変わりする。もし、星空の写真に"Moon"カーネルでRINgプラグインをかけたら、いきなり全ての星が三日月に早変わりだ。また、"Smile"カーネルであれば、いきなり光が大小様々な「笑顔」に早変わりする。そんな風にして、色んな画像ファイルを演算カーネルにして見ると、色んな景色が見えてくるはずだ。例えば、「星はなぜ星型に見えるのか」のグループが作成した「星型シミュレーションソフトウェア」の出力結果を演算カーネルにすれば、目の前の景色が星空の向こうの景色に早変わりするだろう。そしてまた、水で満たしたコップの向こうに浮かぶ光の画像を使えば、RINgはデジカメで撮った色々な写真を水槽の向こうの景色であるかのように描き直したりするかもしれないし、あるいはまたまるで瞳に涙を浮かべながら景色を眺めてみたかのように描き直したりするかもしれない。

