1998-01-08[n年前へ]
■Photohoの乱数プラグインを作成する 
「2項分布のムラについて考える」の関連して、Photoshopの乱数プラグインを作成したのでメモしておく。 PhotShopはとても便利なソフトである。画像を取り扱うにはトップクラスと言っても良い。あえて、難を挙げるならば8Bit階調が基本という所である。もちろん、12bit階調なども扱えるのは知っているが、基本機能とは言えないと思う。
しかし、PhotoShopで凝ったことをしようとすると、Pluginを作らざるを得ない。PhotoShopでPluginをつくるには2つのやり方がある。それは、
- Adobe提供のPlugin SftwareDevelopmentKitを使ってPluginを作る。
- FilterFactoryを使ってPluginを作成する。
今回はランダムノイズをつくるためのプラグイン作成が目的である。その程度であれば、FilterFactoryを使うのが簡単で良い。
 | まずは、FilterFactoryを使う。 |
まずは、Redチャンネルにのみ乱数を与えるものをつくる。以下がそのパラメータである。
 | たった、これだけである。 Redに乱数を与え、Green,Blueのチャンネルには0を与える。 |

もうひとつ、各色に乱数を与えるプラグインのサンプル画像はこのようになる。

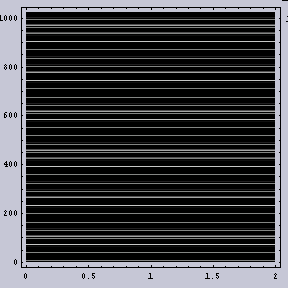
さて、試しに使ってみる。1000x1000ドットのランダムノイズ画像を作成してみる。その画像はここに載せるには大きすぎる。そのため、その一部を左下に示す。その画像に対して各領域10x10の100ドットで平均し、100x100に変換した画像を右に示す。詳しくは「2項分布を考える」を見て欲しいが、100ドットで平均したくらいではフラットにはならない。それどころか、有限のいくら広い範囲で平均しても正確にはフラットにはならない。もし、フラットになるのであれば、それはランダムな2項分布ではない。もちろん、PhotoShopの丸め誤差とかの話は別にしておく。また、「2項分布を考える」の際は1次元の1成分データであったが、今回は2次元3成分データである。そのため、人間にはよりフラットに見えにくい。相対的な色差に対しては人間の目は敏感だからである。
 |  |
今回の例も「2項分布の特性:どんなに広い領域であっても、領域中の平均が一定でない」の当然の結果である。仮に、ある広い領域中の平均が一定であるような確率過程を用いればこのようなことは生じない。もしも、そのような確率過程に基づくものがあったら、部分部分はランダムに見えても、広い領域ではフラットに見えるのである。
1998-12-27[n年前へ]
■Wveletで周期解析をしてみる 
音声・地震などの1次元信号や、画像等の2次元信号処理の解析というのはなかなか面白そうだ。そこで、周期ムラに対してWaveletをかけて周波数解析をする練習をやってみたい。また、短時間フーリエ変換とWaveletの比較もしてみたい。音声・地震などのデータはまた別にやってみることにして、今回は画像データを扱うことにする。ただし、いきなり2次元も何なので、画像データの周期(つまり1次元的な振動)に注目して、解析を行ってみたい。
まずは、「周期ムラのある画像」と「周期ムラのない画像」の2種類の画像を作成する。画像はいずれも数式を用いて作成した。X方向に変化する縞模様であり、表.1のような演算式になっている。一応、2次元画像ではあるが、Y方向にはなんの変化もない。2つの数式を見比べてみると判るが、いずれも2項からなり、低周波数のSinと高周波数のSinからなっている。「周波数ムラのある画像」では、その低周波数のSinの中にさらにSinがあるので、周波数がある周期で変化していることになる。一見、「周波数ムラのない画像」の方でも低周波数のSinの内部にさらにSinがあるように見えるが、0が掛けられているので、実際には存在しないのと同じである。
| 2つのSinからなり、その一方のSinの周期がムラ(一定の周期)をもっているもの。第二項目のSinの内部にさらにSinを入れることにより、周波数ムラを作っている。 | 2つのSin波からなり、どちらの周期も正確なもの。第二項目のSinの中のSinは0をかけてあるので、何ら影響を及ぼさない。 |
そのような数式に基づいて作成した画像を図.1に示す。なお縦軸がX軸であり、横軸がY軸である。図.2(b)では周波数ムラはないが、2つの周波数成分から作成されているため、うねりが生じている。
 |  |
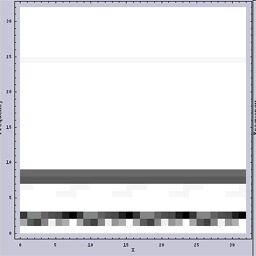
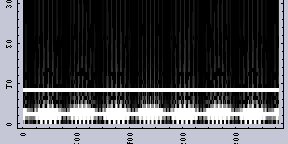
まずは、Wavelet変換である。図.2がその結果である。縦軸が周波数を示している。縦軸の上方向が高周波を示し、下方向が低周波を示している。また、横軸が原画像のX方向である。白は強度が小さいことを示し、黒は強度が強いことを示している。
いずれの画像も2つの周波数成分からなることが一目瞭然である。また、図.2(a):「周波数ムラのある画像」の方では低い周波数成分の方が、さらにある周期で周波数が変化していることがわかる。
 |  |
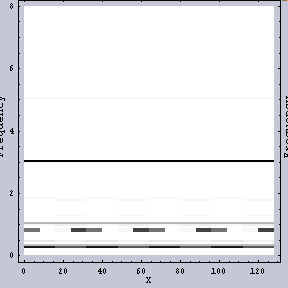
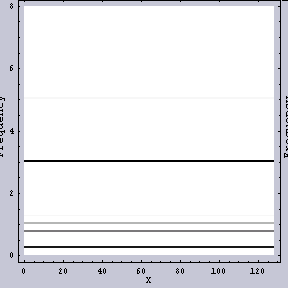
同じWavelet変換でも異なるFilterを用いてみると、結果は異なる。例えば、図.3がその例である。こちらの方が「周波数ムラ」がどのように生じているかを見るにはいいかもしれない。
 |  |
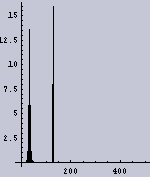
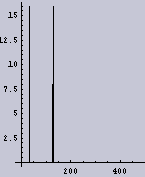
それでは、Wavelet変換ではなくて、フーリエ変換を用いて周波数解析を行ってみる。先ほどの1次元データの全領域に対してフーリエ変換をかけてみる。その結果が図.4である。ここで、横軸が周波数を示し、右側が高周波数を示し、左側が低周波数を示している。縦軸は強度である。
このフーリエ変換の場合も、2つの画像が2つの周波数成分からなり、図.4(a):「周波数ムラのある画像」では低周波数成分がぶれているのはわかる。しかし、その周波数ブレがどのようなものであるかまでは、わからない。
 |  |
なお、単純のためにウィンドー処理はしていない。そのために悪影響は当然出てしまう。
 |  |
単なる全領域にわたった周波数解析と、位置と周波数が同時にわかる解析の違いは非常に大きい。使いこなすのはなかなか難しそうだが....
1999-01-10[n年前へ]
■宇宙人はどこにいる? 
画像復元を勉強してみたい その1
知人から「自称UFO写真」というのものが冗談半分(いや100%位か)で送られてきた。その写真はボケボケの画像なので何がなんだかなんだかわからない。そこで、ぼけぼけ画像を復元する方法を勉強してみたい。UFOは冗談として、画像復元において進んでいるのは天文分野である。そこで、このようなタイトルなのである。もちろん、画像復元の問題は奥が深すぎるので、じっくりと時間をかけてみる。今回はMathematicaを使って試行錯誤を行った。
ボケ画像を復元するには、ボケ画像がどのように出来ているかを考えなければならない。そこで、ごく単純なぼけ画像を考えてみる。まずは以下の画像のような場合である。
 |  |
 |  |
画像:1のような点画像が、画像:2のような分布のボケ画像になるとすると、次のような関係が成り立つ。
(式:1) 画像:4 = 画像:3 * 画像:2
画像:1のような点画像が画像:2になるなら、それを参照すれば、画像:3のような点画像の集合がどう
ボケるかは計算できる。つまり、それが画像:4になる。ここで、*はコンボリューションを表している。
よくある信号処理の話で言えば、画像:2はインパルス応答である。といっても、これはごくごく単純な場合(線形シフトインバリアントとかいろいろ条件がある)の話である。まずはそういう簡単な場合から始めてみる。
このようなごく単純な場合には
(式:2) 画像:3 = 画像:4 * (1/画像:2)
とすれば、画像:3を復元できることになる。
そこで、まずは単純な1次元データで考える。下の画像:5のようにボケる場合を考える。ここでは、ガウス分布にボケるようにしてある。
 |
であったが、* すなわち、コンボリューションは
逆フーリエ変換(フーリエ変換(オリジナル画像) x フーリエ変換(ボケ具合))
と表すことができる。つまり、周波数領域で掛け算をすれば良いわけである。
 |  |
それでは、試しに適当な1次元データをつくって、画像:6とコンボリューションをとってやり、ボケさせてみる。
 |  |
逆フーリエ変換(フーリエ変換(画像:9) / フーリエ変換(画像:7))
= InverseFourier[Fourier[Image8] / Fourier[Image6]]; (*Mathematica*)
とやると、次のデータが得られる。
 |
(式:2) 画像:3 = 画像:4 * (1/画像:2)
を見るとわかるが、画像:2が周波数領域で0になる点があったりすると、計算することができない。また、0に近いとむやみな高周波数の増幅が行われて使えない。
そこで、この方法の修正として、ウィーナフィルターなどの最小平均自乗誤差フィルターがある。これにも多くの不自然な条件のもとに計算される(らしい)。しかし、infoseek辺りで探した限りでは、ウィーナフィルターを用いた画像復元の標準であるらしい。
この方法は先の逆変換に対して、次のように変形されたものである。Mathematicaの表記をそのまま貼り付けたのでわかりにくいかもしれない。
Noise ノイズのパワースペクトル
Signal 信号のパワースペクトル
Boke ボケる様子のインパルス応答
Conjugate 複素共役
BokeData ボケ画像
ResData1 計算した復元画像
Boke1 = (Boke^2 + Noise/Signal)/Conjugate[Boke]; (*Mathematica*)
ResData1 = InverseFourier[Fourier[BokeData] / Fourier[Boke1]]; (*Mathematica*)
である。Noise/SignalはS/N比の逆数であるから、SN比の大きいところではインバースフィルターに近づく。また、インバースフィルターの計算不能な点が消えている。
これを使って復元してみたのが、次のデータである。
 |
まずは、ボケのフィルター(PSF=PointSpreadFunction(どのようにボケるかを示すもの)、2次元のインパルス応答)である。
 |
 |  |
 |
その他線形の画像復元法をいくつか調べたが、ウィーナフィルターやインバースフィルターとほとんど同じような物が(素人目には)多かった。そこで、ウィーナフィルタなどとはやり方がかなり異なるものについて、いずれ挑戦してみたい。
関係はないが、ウィナーと言えばサイバネティクスが思い浮かんでしまう。当然、ロゲルギストが連想されるわけだが、文庫本か何かで岩波版と中公版の「物理の散歩道」が安く売り出されないのだろうか?売れると思うんだけど。新書版は高すぎる。
宇宙人はどこにいるか? そういった話は専門家に聞いて欲しい。わからないとは思うが。
さて、ここからは、1999.01.24に書いている。シンクロニシティとでも言うのか、今回の一週間後の1999.01.17に
日本テレビ系『特命リサーチ200X』で
地球外生命体は存在するのか?( http://www.ntv.co.jp/FERC/research/19990117/f0220.html )
という回があった。何とこの回のコメンテーターは先の専門家と同じなのだ。偶然とは面白いものだ。
1999-01-14[n年前へ]
■ボケたエアーブラシで細かな字がかけるか? 
画像復元を勉強してみたい その2
「宇宙人はどこにいる? - 画像復元を勉強してみたい その1-」ではボケた画像からオリジナルのシャープな画像を復元してみた。前回の話を例えて言うと、
- 太郎君が細かい字をエアーブラシで書いた。
- ボケボケのエアーブラシを使ったから、ボケボケの画になった。
- そのボケボケの画から、太郎君が何を画こうとしたか、考える。
ということであった。
今回、やってみたいのは以下のようなことである。
- 太郎君は太いエアーブラシで字を書きたい。
- しかも細かな字を書きたい。
- そんなことができるか?
直感的には、ボケボケのエアーブラシで細かい字など書けないように思う。その直感が正しいか調べてみたい。考え方は前回と同じく、
出力画像から、ボケ分布でデコンボリューション処理により、オリジナルの画像を計算する。
というやり方である。前回と違うのは出力画像がシャープな画像(先の例で言うと、細かな字)である、という所である。道具は今回もMathematicaを使う。
出力したい画像ファイルを読み込む。
<< Utilities`BinaryFiles`
StreamFile = OpenReadBinary["E:\jun\private\dekirukana\ufo\ufo.raw"]
ImageData = Table[ ReadBinary[ StreamFile , Byte] ,{x,64},{y,64}];
ListDensityPlot[ImageData,Mesh->False,PlotRange->{0,255}]
 |
この細かな字を太いボケボケなエアーブラシで字を書けるか考える。
まずは、エアーブラシのボケボケ度をつくる。
(*正規分布=ガウス分布によるぼけパラメータを作成する*)
δ=10;
μ=32;
ListPlot3D[NormalBoke,ColorFunction ->Hue,Mesh->False,PlotRange->All]
 |
ボケボケの太いエアーブラシである。
デコンボリューション用にガウス分布の場所をずらす。
NormalBoke = RotateRight[NormalBoke,32];
NormalBoke = Transpose[ RotateRight[Transpose[NormalBoke],32] ]; (*上へShift*)
ListPlot3D[NormalBoke,ColorFunction ->Hue,Mesh->False,PlotRange->All]
 |
出力画像をエアーブラシのボケボケ度でデコンボリューションする。そうすれば、太郎君がどのように画を画けば良いかがわかる。はたして答えはでるのだろうか?
計算してみると答えが出てしまう。
SharpImage = Re[InverseFourier[ Fourier[ImageData] / Fourier[NormalBoke]] ];
ListDensityPlot[SharpImage/4,Mesh->False,PlotRange->All]
 |
まず、本当にこれ(画像:4)にそってエアーブラシで画を画くと出力画像(画像:1)が再現できるか確認してみる。そこで画像:4と画像:3でコンボリューションしてやる。太郎君に実際にエアーブラシを使って画を画いてもらうわけである。
それでは、画いてみる。
ResImage = InverseFourier[Fourier[SharpImage] Fourier[NormalBoke]];
ListDensityPlot[Re[ResImage],Mesh->False,PlotRange->All]
 |
画像:1が再現できた。つまり、太いボケボケのエアーブラシで細かい字が書けてしまうわけである。直感的には納得しがたい結果である(私だけかもしれないが)。
これには実はタネがある。画像:4を鳥瞰図でみると判るが、画像4は正負の値が高周波で並んでいる。
ListPlot3D[SharpImage/4,ColorFunction ->Hue,Mesh->False,PlotRange->All]
 |
太郎君が使ったエアーブラシは太いボケボケのエアーブラシではあるが、吹き量に正負が両方ともあったのである。そのようなエアーブラシを使うと太郎君の腕(高テクニシャン)ならば細かな字が書けるわけだ。どんなパターンもかけるかはどうかまでは知らないが、少なくとも"hirax"という字は画ける。
前回のような光学系の例でも、これが何に対応しているかはすぐわかるが、一番分かりやすいのは電荷と電位の例だと思う。
電荷が周囲につくる電位分布はボケボケの分布である。ところが、金属などを適当に配置して、その金属に電位を印加してやると、鋭い電位分布をつくることができる。つまり、ボケボケの分布から鋭い電位分布を作成してやることができる。こちらなら直感的にもすぐ納得できるだろう。その際には、金属表面に電荷が鋭く集中するのも、よく知っている話だ。
実感用に電場計算を行った例を以下に示しておく。使った道具はCUPSの電場計算プログラムである。CUPSは教育用のプログラム集である。
一応、2次元膜の例で、金属を配置し、適当に電位を印加し、電位・電荷量計算を行ってみる。
 |
もちろん、金属内部では均一な電位である。それを条件に解いているのだから当たり前だが。
その時の電荷分布を下に示す。金属表面に鋭い電荷分布が生じているのがわかるだろう。
ここでは大雑把な金属の配置にしてしまったが、格子状の金属配置にして、互い違いに違う極性の電位を印加すれば(細かい字に相当する)、正負の極性の電荷分布が鋭く現れるのは当たり前の話だ。
 |
電位、電場、電荷量を一緒に示しておく。
 |
今回の話は、単なる計算上の話である。それに、何かどこかで仮定を間違っているような気もするんだよなぁ。信用度アルファ版だからまぁいいか...
1999-02-27[n年前へ]
■画像ノイズ解析について考える 
考える理由
画像ノイズ解析を目的として、2次元フーリエ変換を用いて周波数解析をすることが多い。かねがね、このやり方について疑問を感じていたので少し考えてみたい。その疑問とは次のようなことである。
- 通常の2D-FTでは、入力データ全領域での周波数解析を行う。従って、単発のパルスのようなノイズはバックグラウンドに埋もれてしまい、結果にはなかなか出てこない。
- 同じ理由で、2D-FTでは位置と周波数解析を同時に行うことができない。(もちろん、短時間フーリエ関数を使えば、そのような測定は行うことができる。)
- また、ホワイトノイズのようなフラットな周波数特性を持つノイズもバックグラウンドを押し上げるだけの効果しか持たないため、解析をしづらい。
2D-FTと2D-Waveletの例
はじめに、2D-FTと2DWaveletの例を挙げる。まずは2D-FTである。 |  |  |
このように、2D-FTの結果というのは周波数(X,Y両方向)と振幅がわかる。ここでのスクリーン角のような周期性を持つものの解析にはフーリエ解析というのは極めて有効である。店で見かけるインクジェットプリンターもヘッドの移動による周期ムラが激しいが、このようなムラに対してフーリエ変換を用いた周波数解析を行うのは正当であり、有効だろう。
それでは、同じ画像に2D-Waveletをかけてみる。2D-Waveletの結果は位置と周波数強度分布情報(ホントは違うのだが)が両方出てくる。位置情報が2次元で周波数強度分布情報が1次元であるから、合わせて3次元である。そのため、表示に一工夫いる。
第一段階として高周波成分から調べてみる。すぐにこの結果の意味がわかるだろうか?
 |  |
| 高周波のX成分 | 高周波成分 |
| 低周波成分 | 高周波のY成分 |

もう何分割かしてみる

なお、フーリエ変換では基底関数としてSinが用いられるが、Wavelet変換では基底関数としていろいろな関数を使うことができる。今回はDaubechiesの4次のものを用いている。下がその形である。
 |
ドットのノイズを解析してみる
それでは、今回の本題に入る。以下が原画像である。左が「2つの大きなドットからなる」画像であり、右がそれにノイズの加わった「ノイズ」画像である。ここでノイズはホワイトノイズを加えているつもりである。ドットは周期性を持つデータだが、ノイズ自体は周期性を持たない所がミソである。また、ここで言う「ノイズ」とは現実の現象とは何ら関係がない。単なる例えである。 |  |
 |  |
右のノイズの加わった画像の2DFTの結果では、広い周波数領域で強度が上がっている。しかし、下の鳥瞰図で示した(私は立体が好きなのだ)方でもわかると思うが、バックグラウンドが持ち上がっているだけである。いずれにせよ、あまり左右の間で違いはない。今回のような64x64の画像ではなく、もっと大きい画像ではその違いははより識別不能になる。
 |  |
 |  |