1998-01-08[n年前へ]
■Photohoの乱数プラグインを作成する 
「2項分布のムラについて考える」の関連して、Photoshopの乱数プラグインを作成したのでメモしておく。 PhotShopはとても便利なソフトである。画像を取り扱うにはトップクラスと言っても良い。あえて、難を挙げるならば8Bit階調が基本という所である。もちろん、12bit階調なども扱えるのは知っているが、基本機能とは言えないと思う。
しかし、PhotoShopで凝ったことをしようとすると、Pluginを作らざるを得ない。PhotoShopでPluginをつくるには2つのやり方がある。それは、
- Adobe提供のPlugin SftwareDevelopmentKitを使ってPluginを作る。
- FilterFactoryを使ってPluginを作成する。
今回はランダムノイズをつくるためのプラグイン作成が目的である。その程度であれば、FilterFactoryを使うのが簡単で良い。
 | まずは、FilterFactoryを使う。 |
まずは、Redチャンネルにのみ乱数を与えるものをつくる。以下がそのパラメータである。
 | たった、これだけである。 Redに乱数を与え、Green,Blueのチャンネルには0を与える。 |

もうひとつ、各色に乱数を与えるプラグインのサンプル画像はこのようになる。

さて、試しに使ってみる。1000x1000ドットのランダムノイズ画像を作成してみる。その画像はここに載せるには大きすぎる。そのため、その一部を左下に示す。その画像に対して各領域10x10の100ドットで平均し、100x100に変換した画像を右に示す。詳しくは「2項分布を考える」を見て欲しいが、100ドットで平均したくらいではフラットにはならない。それどころか、有限のいくら広い範囲で平均しても正確にはフラットにはならない。もし、フラットになるのであれば、それはランダムな2項分布ではない。もちろん、PhotoShopの丸め誤差とかの話は別にしておく。また、「2項分布を考える」の際は1次元の1成分データであったが、今回は2次元3成分データである。そのため、人間にはよりフラットに見えにくい。相対的な色差に対しては人間の目は敏感だからである。
 |  |
今回の例も「2項分布の特性:どんなに広い領域であっても、領域中の平均が一定でない」の当然の結果である。仮に、ある広い領域中の平均が一定であるような確率過程を用いればこのようなことは生じない。もしも、そのような確率過程に基づくものがあったら、部分部分はランダムに見えても、広い領域ではフラットに見えるのである。
1999-01-08[n年前へ]
■2項分布のムラについて考える 
今回の目的を説明するために、少し準備を行う。
まず、2048個の[ランダムに0から256の値を持つもの]からなる1次元データを作成する。以下の左図がそのデータである。ここで、X軸がデータの順番であり、1から2048までを示し、Y軸がデータの値である。Y軸の数値ラベルは0から256の値である。折れ線グラフの方が1次元データとして実感できるのだが、そうすると真っ黒になってしまうので、点プロットグラフにしてある。
また、[0から256]のデータの出現頻度のグラフ(つまりヒストグラム)を右の図として示す。
 |  |
右のグラフを見ると、下は2回から上は15回位の間で出現頻度がばらついている。その頻度のムラは分散として計算することができる。今回の場合は2項分布である。
今回の目的は、そのムラを考えることである。広い範囲で見たときには、どの程度フラットだろうか。例えば、最初の100個のデータの平均と、次の100個のデータの平均というのはどの程度同じだろうか。それが1000個ならどうだろうか。1000個平均してみても場所によって、平均値はばらついているだろうか。もし、ばらついているとしたら、2項分布の確率過程を導入すると、広い範囲で見てみても認識できるくらいのばらつきを導入していることになる。その「ばらつき=ムラ」を人間が感じないためには、どの程度まで平均しなければならないのか。そういったことである。
ここで、先の2048個の1次元データは2048dpiの1次元画像データである、ということにしてみる。したがって、X軸の領域はトータル1inchを示すことになる。そして、以下の作業をする。
- 2048dpiの1次元画像データを2値化(128でしきい値とした)したものを8個に分断する。
- それぞれ、分断したデータ(256個)内で平均を取る。そなわち、8ppi(pixelper inch)の1次元データができる。
 |  |
すると、2048dpiの(1/2の確率で2値化された)データというものは、今回の目的である「ムラを感じないための条件」を満たしていないということになる。ここでは画像に例えているが、別に画像だけの話ではない。
それでは、いくつか条件を振ってみたい。各々の条件下で示すグラフの領域は以下を示す。
| オリジナルの1次元データ | 左のヒストグラム。条件違いで軸が揃ってないのに注意。 |
| 8ppiに変換したもの Y軸はいずれも相対値であることに注意。Max=256と読み直す。 | 左のヒストグラム X軸はいずれも相対値であることに注意。Max=256と読み直す。 |
オリジナルの1次元データ | 左のヒストグラム |
8ppiに変換したもの | 左のヒストグラム |
オリジナルの1次元データ | 左のヒストグラム |
8ppiに変換したもの | 左のヒストグラム |
オリジナルの1次元データ | 左のヒストグラム |
8ppiに変換したもの | 左のヒストグラム |
上の右下で出ているようなヒストグラムが2項分布であることは、サンプルを多く(しかし、試行回数を少なく)すればよくわかる。例えば、このようになる。


今回の話はあることの前準備なので、これだけでは話しが全く見えないかもしれない。というわけで、
1999-09-17[n年前へ]
■モアレ、デバイス、2項分布の三題話 
淡色インクの副作用
今回は、9ヶ月間も寝かせた伏線にまつわる話である。いや、別に寝かせるつもりは無かったのだが、いつのまにかそんなに時間が経ってしまった。
以前、
という話があったが、その2つを結びつけるミッシングリンクについて考えてみたいと思う。「2項分布のムラについて考える(1999.01.08)」の最後に「今回の話はあることの前準備なので、これだけでは話しが全く見えないかもしれない。というわけで、続く...」と書いた。「その続き」というわけである。始めに「2項分布のムラについて考える(1999.01.08)」の要点をまとめると以下のようになる。それは、
- ランダムと呼ばれるものの内で代表的な2項分布においては、当然のごとく「ある領域での平均値はばらつく」。
- そして、そのばらつきは直感的に考える程度よりももっとばらつく。
- 例えば、2値画像で考えるならば、2048dpi程度の解像度でランダムなデータを並べた場合には、人間の目はざらつきを感じてしまう。
そして、「モアレはデバイスに依存するか?(1998.11.20)」での要点は
- モアレにはデバイス依存性がある
- 線形な重ね合わせが成り立たない場合にはモアレが発生する。
最近のインクジェットプリンターはCMYKの4色インクだけでなく、淡色インクも使うものもある。淡色のインクを使うことで階調豊かな画像を印字できるわけだ。4色インクだけではディザなどを使って、解像度を下げて階調を出さなければならないわけであるが、それが不要になるわけだ。
解像度を下げないですむわけであるから、ディザのざらつきを感じないですむわけだ。しかし、淡色のインクを使った場合の効果というのはそれだけではないように思われる。HP(ヒューレッドパッカード)などのWEBのプリンター紹介を読んでいると、「淡色のインクを重ねて濃度を出す」というような記述を目にする。これは「少なくとも淡色インクでは線形性(あるいはそれに近い関係)が成り立つ」ということだ。
インクジェットプリンターの解像度を上げたときに、インク滴が意図しないところへずれてしまうことはきっとあるだろう。その際に他のインク滴と重なったらどうなるだろうか?意図しなくても他のインク滴との重ね合わせは発生してしまうだろう。
重ね合わせが成り立たない、非線型なインクではモアレが発生する。言いかえれば、意図しない濃度のばらつき・ざらつきが発生してしまう。「2項分布のムラについて考える(1999.01.08)」で考えたようにランダムに重ね合わさるから広い領域では一定だろうというのは予想外に成り立たないのである。でたらめというのは私の予想外に大きく効いてくるのである。
しかし、重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しないことになる。参考までにインクジェットの印字画像の拡大写真を示してみる。
 |  |
「重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しない」と、書いただけでは意図するところが伝わらないと思うので、「モアレはデバイスに依存するか?(1998.11.20)」で使った画像を用いて考えてみる。この画像は重ね合わせがある幾何学模様で生じているが、この現象がランダムに起こっているものとして読み替えて欲しい。
 |  |  |
下は、淡色のインクで重ね合わせ(インク滴の意図しない重なり)が生じた場合である。
 |  |  |
なんの模様も生じていなく、意図した通りの画像出力ができているのがわかると思う。
ということで、今回の話(というか前の2回の話)の繋がりは、
淡色のインクを用いたインクジェットプリンターでは、意図しないインク滴の重ね合わせが生じてしまっても、濃度変化が生じにくく、意図しないインク滴の重ね合わせがでたらめに発生してしまったとしても、画像にはあらわれない可能性があるということである。
うーん、マニアックな内容だ。「身近な疑問を調べる」という看板に偽り有り、である。しかも単なる推論だ。
しかし、もしもインクジェットプリンターを買う人がいるならば、淡色のインクを使っているものを購入するといいかもしれない、ということがわかっただけでも良しとしておこう。
2000-05-02[n年前へ]
■モアレがタネの科学のふろく 
うれし、懐かし、学研の科学
先日、友人夫妻で面白いものを見せてもらった。そこで、すかさずオネダリをして手に入れてきた。それが下の写真のものである。
 |
これは学研の科学の学習教材である。「科学の学習教材」というよりは、「科学のふろく」といった方が通りが良いかもしれない。この写真のものは「6年の科学 1998年1号 トリックトランプ「マル秘」超魔術13」である。これを私にくれた友人(妻の方)は「学研教室」の「先生」をやっているので、こういう面白いものを持っているのである。
残念ながら、付録の一部だけで、中身が全部揃っているわけではない。それに加えて、本誌もない。そこで、手元にある材料からトランプトリックを想像しなければならない。しかし、その想像しなければならないところが、また面白いのである。手品の「タネ」を想像し、実際に検証できるのだから、楽しくないわけがない。
こういう理系心をくすぐる、懐かしいものというのは色々ある。以前登場した、学研の電子ブロックもそうであるし、雑誌の「子供の科学」もそうだ。そういった中でも、この学研の科学のふろく(学習教材)はその最たるものだろう。こういった、科学の付録は学研のサイト内の
- 科学の付録 (http://kids.gakken.co.jp/kagaku/furoku/index.html )
さて、今回の「6年の科学 1998年1号 トリックトランプ「マル秘」超魔術13」のネタ探しをしていると、面白いものを見つけた。それが下の写真である。何にも書いてないトランプに半透明シートをかけると、アラ不思議、ハートの5が現れるのである。
 |
この「魔法のトランプ」のタネはもちろん「アレ」だ。「できるかな?」にもよく登場してきた「モアレ」である。これまで、
- モアレはデバイスに依存するか?(1998.11.20)
- OHPによるモアレと光の干渉の相似について考える。 -ヒラックス・ディザの提案 - (1998.11.22)
- モアレ、デバイス、2項分布の三題話- 淡色インクの副作用 - (1999.09.17)
このトランプの表面の模様を拡大してみるとこんな感じになる。これは「ハートの先端部分の拡大写真」だ。赤い線によるハーフトーンパターンが変化している部分(実はハートマークの先端部分)があるのがわかる。この模様は結構細かく、400線/inchくらいである。
 |
このようなトランプに、黒い斜線が描かれた半透明シートをかぶせると、モアレが発生して模様が見えるわけである。下の写真が、トランプに半透明シートをかぶせたところである。半透明シートには実は黒い斜線模様が描かれていることがわかる。
 |
そして、トランプの模様と半透明シートの模様の間でモアレが発生して、その結果として「5」
の文字が浮かび上がっているのがわかると思う。
このトランプのタネのような画像を自分でも適当に作ってみることにする。やり方はとても簡単である。ハーフトーン模様を作成して、模様を書いて、模様部分だけハーフトーンを変化させてやればいいだけである。そして、元のハーフトーンと重ね合わせてやれば、模様が浮き上がるのである。こういう細工をしないと読めない画像を使って、何か面白いことをできるかもしれない。
 |
 |
 |
一応、モアレはデバイスに依存するか?(1998.11.20)の時のように今回も二つの画像の重ね合わせの時に、線形性が成り立つ場合と、成り立たない場合の比較をしておく。
先のAとBを重ね合わせてみたもの  |
線形性が成り立つ場合には、モアレが発生していないのがわかる  |
つまり、非線形性を持つ場合 この場合にはモアレが発生する  |
今回の場合も当然、線形性が成り立つ場合にはモアレが発生しないのがわかると思う。今回のトランプ手品も、半透明シートとトランプの模様の間の重ね合わせの非線形性を利用していたわけである。
この線形性と非線形性の重ね合わせの違いも利用してみれば、もっと新しい何か面白い手品やおもちゃのネタになるかもしれない。インクジェットプリンターの淡色インクと、濃いインクの違いを利用して何か面白いトリックはできないだろうか?
さて、先の知人夫妻は共に「先生」である。なので、時折子供に「どうやって教えるか」という話になることがある。子供という「タネ」をどうやって育てていくか、という話である。子どもが人から言われたことでなく、自分で調べて何かを覚えるにはどうしたら良いか、などだ。もちろん、それは「先生」もまた同じである。人に言われたことを鵜呑みにするのではなく、自分で「実感する」のはむしろ子どもより「先生」の方が難しいかもしれない。
私も先日あるメーリングリストで
「先々」のある(製造業に携わる)子ども・青年などわずかでしょうという言葉を見てしまって以来、そういったことについて色々と考えてしまうことが多いのであるが、こういう「タネ」つながりについて考えているのも面白いかもしれないな、と思うのである。
2000-12-24[n年前へ]
■A型vB型・大戦争 
血液型分布を眺めてみよう
今年も私の職場には新入社員が入ってきた。その新入社員の中の一人は「血液型+ 動物占い」の信者だった。何しろ、ことあるごとに「血液型 + 動物占いの結果が同じ人はとってもよく似ているんですよ!もうビックリするくらい当てはまるんですよ!もちろん、たま〜に例外の人もありますけど。」といつも私たちに言うのである。もちろん、私も含めてその周囲の人は「その自信と根拠は一体どこからくるんだぁ!」とツッコミを入れるわけであるが、少なくとも本人は気持ち良いくらい自信満々なのである。とはいえ、私も占いというものは「根拠無しにテキト〜に何かを決めつけることができるという素晴らしいもの」だとも思うので、まぁそれはそれで楽しいわけだ。そんな血液型大好きな新入社員なら可愛いものであるが、それがもう少しエラ〜イ人になるとちょっとばかり大変である。私のとなりの部署の部長なども実はそんな血液型信仰者なのであるが、その部の配属には血液型が参考にされるというオソロしくも確かな真実がある(ホントにホント)。そこの某部長曰く「B型は実験が杜撰だから嫌い。」という実に誠実な理由に基づき、その部はA型人間大集合なのである。というよりも、その部からB型は外されているのだ。恐るべき純血追求型人事手法である。ヒットラーもビックリである。
そんなA型人間大集合の部がある一方で、私が所属している部屋(課)は何故かB型が多い。10人強の中で半数程がB型なのである。どこで読んだのか忘れたが、日本人の血液型はA型35%,B型 25%,AB型 10%,O型 30%位であるらしいから、私の課のB型比率はかなり高い。しかし、もちろんそれは単なる偶然だろう。隣の部がB型を排除しているから私の部屋がB型で溢れているのじゃないか、という恐ろしい想像ができないこともないが、そういうわけでもないだろうと私は信じたい。
しかし、「信じたい」という気持ちだけで物事を決めつけるのは危険この上ない。それは「セーラー服の女子高生はみんな可愛くて純真だと信じたい」という危険さと同じくらいデンジャラスである。何事も、先入観で判断してはイケナイのである。確認することが重要なのだ。そこで、今回は「10人強の中で半数程がB型なんていうのはよくある偶然」だということを血液型分布・配置シミュレーション(超手抜き)でも行って確認してみたいと思うのである。そして、私が所属している部屋(課)にB型が多いのがただの偶然であること、つまりある特定の血液型の人間が集まることが不自然ではないことを確認してみたいのである。
さて、今回の血液型分布・配置シミュレーションのやり方は次の通りだ。
- まずは256人の人間を用意する。
- その256人に対して、A型 35%,B型 25%,AB型 10%,O型 30%位になるようにAB型の抗原(AA,AO,BB,BO,AB,OO型)を配置する。
- その後、遺伝子を移動して血液型を再配置する。
- 近所の人間と子供を作る(遠距離恋愛は考えない)。
- 血液型分布・配置を調べる。
この説明の中で、一言で「遺伝子を移動して、近所の人間と子供を作る」と書いたが、もちろんその現象の中には
- 人が引っ越したり・移動したりしていったり、
- 愛が芽生えて子供がデキたり、愛が芽生えないけどデキちゃったりして子供が出来たり、
まぁ、しかしカマキリのようにエッチのあとにメスがオスを食べちゃう動物もいたりするのだし(実際のところは知らないけど)、この恐怖の「子供が一人出現すると親が一人消えてしまう」システムもそんなに不自然ではないのである、ということにしておこう。というわけで、いつもながらの強引な展開だ。
そんなわけで、行ってみた血液型分布・配置シミュレーションの結果が下の動画である。一マス一マスが一人の人間である。時間毎にどんどん血液型分布・配置が変化していく様子が判ると思う。ちなみに、
赤 = A型、緑 = B型、水色 = AB型、紫 = O型である。
 ファイルサイズがデカイのは直すつもり… |
この結果はカラフルにただチカチカするだけの計算結果ではないのである。このチカチカこそが人生の喜怒哀楽なのだ。そこを是非とも心して眺めてもらいたい、と切望する次第である。
じゃぁ、時間を追ってA型、緑 = B型、青色 = O型、紫 = AB型(色が一部さっきと逆転していることに注意)がどう変化していったかというと下の図のような感じだ。それほど一定ではないことがわかるだろう。それぞれの血液型の比率が逆転したりする下克上な瞬間だってままあるのである。
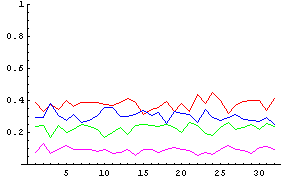 A型、緑 = B型、青色 = O型、紫 = AB型 |
もちろん、これは256人という少ない人数だからこんなに大きく比率が変動するわけである。しかし、今回は「つまりある特定の血液型の人間が集まる」かどうかを調べたいのである。つまり、ある少人数の人間達を考えたときに特定の血液型の比率が多くなることがあるかを調べたいのだから、考える人数は少人数で構わないわけだ。
256人という比較的多い人数を考えた場合ですら、人生のドラマが続く中でそれぞれの血液型比率は結構変化して、それぞれの血液型の比率が逆転したりすることもあるわけだが、じゃぁもっと狭い領域に注目したらどうなるだろうか?例えば、下の瞬間の血液型分布・配置を眺めてみよう。
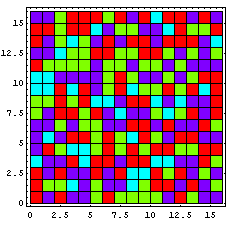 |
おやおや、結構
- A型 = 赤が連続していたり
- B型 = 緑が集まっていたり
- O型 = 紫が多いくせに固まっていたり
- AB型 = 水色が少ないながらも集まっていたり
試しに、先程のシミュレーションである16人(つまり私の部屋(課)の人数位だ)を抽出して調べたときに、A型が一番多かった場合と、一番少なかった場合で、A型の割合だどんなだったかを調べてみたのが次に示すグラフである。ここで、
- 赤 = その瞬間にA型が一番多かったグループにおけるA型の比率
- 青 = その瞬間にA型が一番少なかったグループにおけるA型の比率
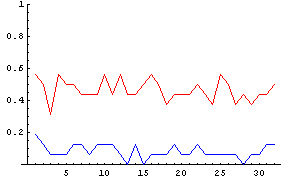 赤 = A型が一番多かったグループにおけるA型の比率 |
なるほど、A型が一番多かったグループではA型の比率が60%を越える時もある。逆にA型が少ないグループでは16人のなかにA型がいない、という状況すらあるのだ。
ということは、私の部屋のB型がほぼ半数という状態だって別に不自然ではなく、それはごく自然なわけだ。もちろん、A型とB型の比率が違うことを考慮しても、全然不自然ではないだろう。ということは、血液型信仰者の某部長による隣の部のB型キライの恐るべき純血追求型人事手法の余波をうけて、私たちの部屋がB型だらけということはなくて、それは単なる偶然だろう、ということがわかるわけだ。
ところで、ここまで書いて「血液型信仰者の某部長」が「ヘンな人」というイメージを持たれてしまうと非常に困る。何故なら、もっと変でなおかつエライ人がイッパイいるのである。(ここでいう「エライ」は関東弁&関西弁のニュアンスだ。つまり、「偉いけど大変な」というニュアンスだ。)血液型信仰者なんてカワイイもんじゃないの、と思えるくらいのスゴサである。だって、ダウジングが超大好きで、奇跡の水が超〜大好きな人だっているのだ。もしかしたら、ダウンジングなんて言葉を知らない人がいるかもしれない。しかし、知らなくて当たり前である。ダウンジングとは下の絵のような棒を持って水脈などの場所捜しをする迷信の中の迷信である。キング・オブ・迷信と言っても良いくらいのアイテムである。
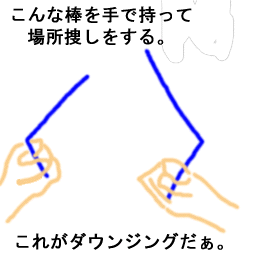 |
しかも、なんとダウジング&奇跡の水大好き人間が実は某新規材料開発部署の責任者だったりするので、そこらへんは考えると実はかなりコワイものがあるのだが、それはそれ、結構笑える事実(ホントにホント)ので良しということにしておきたい。