2009-09-29[n年前へ]
■PIDチューニング機能を追加したSimulink Control Design 
MathWorks、PIDチューニング機能を追加したSimulink Control Designの新版を発売
米MathWorks社（マスワークス、マサチューッセッツ州ネイティック）はこのほど、PID（比例・積分・微分）コントローラのチューニング処理を自動化する機能を追加した「Simulink Control Design 3.0」を発売した。Simulinkの新しいPID Controllerブロックも同時にリリースする。
新バージョンのチューニングアルゴリズムは、必要な位相余裕とシステム帯域幅にもとづきPIDコントローラのゲインを自動的に計算する。また、新しい PID Controllerブロックを使用することにより、PIDコントローラを迅速に作成でき、PID構造の選択、積分器アンチワインドアップロジックの組み込み、連続時間領域から離散時間領域への変換などが可能になる。
2009-12-11[n年前へ]
■エクセルでシミュレーション Vol.9 二次元非定常熱伝導問題の温度変化グラフも作ってみよう
この記事は、「エクセルでシミュレーション Vol.8 二次元非定常熱伝導問題を解こう」の続きです。前回の記事では、比較的薄い円形ベルトが回転するモデルで、ベルトの厚みがベルト内の熱拡散に対して十分に薄いという仮定の下での近似を行ったと考えると）三次元非定常熱伝導問題を解いているとも言えなくない・・・というような二次元非定常熱伝導問題を解く、エクセルの表計算シートを作り眺めてみました。もちろん、VBAはもちろん関数も使わず、ただセル間の加減乗除演算のみで、熱伝導方程式を差分化したものです。
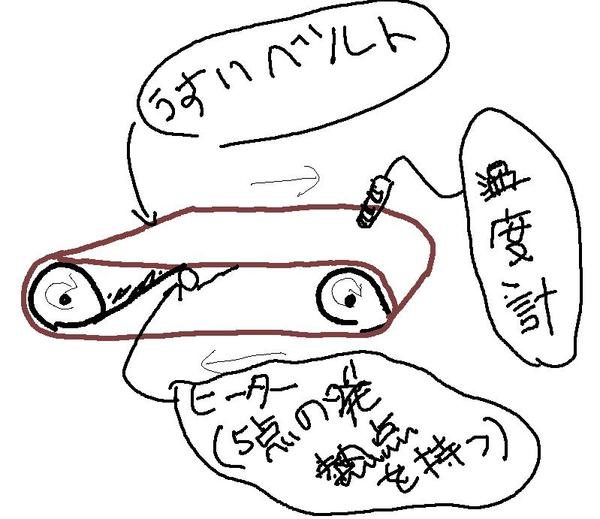
今日は、計算領域の任意の部分の温度変化をグラフにする部分を前回のエクセルシートに追加してみようと思います。つまり、ベルト状に温度センサでも貼り付けたら、時々刻々と一体どんな温度が測定されるのかをシミュレーション計算時に表示させたい、というわけです。
このような需要は非常に多くあると思いますが、一体それをどのようにすれば作ることができるでしょうか？エクセルのシート上は、非定常問題を解いているので、その瞬間その瞬間の温度分布しかデータが残っていないように思われ、スタート時からの温度変化をグラフにするのは難しいように思えてしまいます。
しかし、「ガウスザイデル法でなく、ヤコビ法を用いて反復計算を行うために使ったテクニック」、すなわち、
エクセルは（セル間の循環参照がある場合に用いる）反復（収束）計算時には、表の左上をスタート地点として「Zの法則 」の順序にしたがって（つまり、左上→右、そして一個下の行をまた左→右という順番で）逐次的に解くという計算順序になります。ということを利用すると、「計算領域の任意の部分の温度変化をグラフにする」ということが、いとも簡単に実現できてしまうのです。種明かしは後回しにして、まずはそのようなことをしているエクセルシート動画を下に張り付けてみます。動画の上部分は前回と同じく「回転するベルトを平面上の等高線色付きグラフとして表示したものです。そして、その下にあるのが、「等高線色付きグラフ右横部にある灰色円部分」の温度変化を横軸：時間・縦軸：温度で時系列グラフにしたものです。
下の折れ線グラフを見れば、「等高線色付きグラフ右横部にある灰色円部分」の温度が時間を追って上昇していくようすをよく理解することができるのではないでしょうか。
種明かしはこうです。エクセルのシートのずっと下方（下の行のセルに）"=温度変化を知りたいセル"という式を入れます。ここでいう温度変化を知りたいセルというのは、たとえば、X24といったセルを示す番号です。ですから、実際に（一番下のセルに）入れるのは、"=X24"といったものになります。
そして、そのセルの上にあるセルをクリックし、=と入力した上で、その下のセルをクリックし"Enter"を押します。つまり、一個下の（さきほど"=X24"という式を入力した）セルを参照するようにするのです。そして、そのセルを選択した上で、上の方までズルズルズル～とコピーしてしまいます。
エクセルの（セル間の循環参照がある場合に用いる）反復（収束）計算時の計算順序を考えてみれば、今「ズルズルズル～とコピー」を行った列には、「古い計算結果が上、一番下が最新の計算結果」という順序のデータが格納されていくことになります。（上から下に計算が逐次行われていることを考えると）計算ステップごとに、一個値が上に移動していくので、結果としてそのように時系列的なデータを保持できる、というわけです（結局のところ、ヤコビ法を用いるために、バッファエリアを下に設けたのと全く同じパターンです）。
あとは、計算スタート時点からの（シミュレーション上の）経過時間なども同じように作り、散布折れ線図でも挿入すると、「上記のような「任意の部分の温度モニター機能付きの疑似三次元非定常熱伝導問題を解くエクセルシートのできあがり」となるわけです。もちろん、温度モニターは（上段で行ったことを他のセルに対してもしてやるだけで）いくつでも設置することができます。実に単純・簡単な（けれど巧妙な）実装ですがとても便利な機能です。
さて、ベルトの温度モニター機能も付きましたので、今度はセンシングしたベルトの温度を用いて、ヒーターの温度を（まずは簡単なPID制御でも使って）制御しベルトの温度分布を適正に調節する機能例でも、簡単に実装し（ハードウェアをいじっている）気分にでも浸ってみることにしましょうか。
2009-12-16[n年前へ]
■エクセルでシミュレーション Vol.10 二次元非定常熱伝導問題シミュレーション＋P(ID)制御エクセルシートを作ってみよう
「エクセルでシミュレーション Vol.9 二次元非定常熱伝導問題の温度変化グラフも作ってみよう」で、二次元非定常熱伝導問題を解くシートを使いながら（実用的範囲では三次元問題と大差がない）、ヒーターで回転するベルトを高温にした場合の、その回転ベルトの温度分布がどのように変化していくかを計算し、グラフ化し、さらにベルト中の一部分の温度を時系列的にモニターする機能を付けた、シートで遊んでみました。
そこで、今回は、センシングしたベルトの温度を用いて、ヒーターの温度を簡単なPID制御を使ってフィードバック制御するエクセル・シートを作ってみることにしましょう。
PID制御とは、調整量を（現在の）出力値と目標値との差に比例＝Proportionalした量、その（過去からの）積分=Integralに応じた量、および（その瞬間に次にどのように変化するかという）微分=Differentialに応じた量にしたがって変える制御です。言いかえれば、現在（Proportional）・過去（Integral）・未来（Differential）の挙動に応じて、制御調整量を変えてやろうという制御です。比較的、古典的な制御手法ですが、現在でも、もっとも一般的な制御手法です。
まずは、前回のエクセル・シートでヒーター部分を単純に（計算をさせ始めてから＝回転ベルトに対するヒーターを動かし始めてから）100℃にし続けた場合の計算過程を示してみます。つまり、何の制御もしない場合です。その計算結果が、下の動画です。上の動画で上に示したグラフが、回転ベルトの温度分布を示したグラフです（回転ベルトを切り開いたように温度分布を示しています）。動画中の下の折れ線グラフは（上のコンター図で灰色丸部の温度の時間変化を示したグラフです）。ちなみに、縦軸は0℃から150℃までで、横軸が時間軸です。
下の折れ線グラフを見れば、上のコンター図で灰色丸で示した部分の、温度が時間に応じて上昇し、やがて100℃近くになっていることがわかります。
さて、次にPID制御を行ってみることにしましょう。…とはいえ、最初は簡単のために、「灰色丸で示した部分の温度と目標調整温度である100℃との差をヒーターに足す（ネガティブ・日―ドばっく）」という「P=比例成分=現在の違い」だけを利用したP(ID)制御を行ってみます。つまり、現在の出力と目標出力の差異のみをヒーター出力に（適当な比率で）足し合わせてみるのです。言いかえれば、ベルトの温度が0℃なら、ヒーターを200℃くらいにすることで、急激にベルトを温め温度を調整し、目標温度100度と現在のベルト温度の差が小さくなってきたら、ヒーターの温度を110℃くらいに変えてやる・・・というような制御をしてみます。そんなシミュレーション計算を行ってみた結果が、下の計算結果になります。ちなみに、ヒーターの制御温度はエクセルのシートでB32セルで計算されています。また、灰色丸のセンサ取り付け部分（を示した）の温度を示す下の折れ線グラフは、先ほどと同じく、縦軸は0℃から150℃までの温度を示し、横軸が時間軸となっています。
この結果動画を見るとわかるように、「P=比例成分=現在の違い」だけを利用したP(ID)制御（=積分成分と微分成分を使わない）制御では、ベルトの温度は早く立ち上がりますが、ベルトの温度は振動して、なかなかすぐに安定してくれません。しかも、早く温度を立ち上げようとすると、温度振動は大きくなってしまい、温度振動を防ごうとすると、なかなか温度が早く立ち上がってくれない、という相反する関係になっています。いわば、（ある程度、減衰がある）強いバネと弱いバネの振動と同じような現象が起きてしまいます。
さて、それでは、一体どうしたら良い制御ができるのでしょうか。・・・せっかく、簡易にエクセルのような（表計算＝スプレッドシート・ソフトウェアを使った）熱伝導方程式を使ったシミュレーション計算を行うことができる環境があるわけですから、今回扱ったPID制御のような古典的な制御をもう少し復習してみようと思います。
そして、せっかく熱伝導方程式を計算してみたりしているわけですから、そういった微分方程式（つまり現在から未来を示す式）を使うことで実現できる、最適化制御についても考えてみることにします。
2009-12-29[n年前へ]
■「カルマンフィルタ」と「エクセルで解く2次元非定常熱伝導問題」
正月に、（自分用の）汎用「カルマンフィルタ」ライブラリをRubyとCとExcelで書いてみることにした。たとえば、さまざまなデータ、たとえば、信頼性が低く、誤差の大きなセンサデータや、安定性に欠ける実験データから、現実に近い状態量を推定するツールを作ってみることにした。そして、何か（解析式による）モデル計算や各種シミュレーション計算と比較をしてみたり、それらの計算改善へのフィードバック例を作ってみよう、と考えた。
そこで、扱う題材を考えつつ、実際に上記のようなことを行っている例を探してみた。すると、たとえば、
といったものがある。これらの記事が（下に張り付けた動画でその一端がわかると思うが）実にわかりやすく・面白くて楽しく・役に立ちそうに見える。何というか、つまるところ、魅力を持つに必要な三拍子がすべて備わっている。
先日、「２次元非定常熱伝導問題を解く」エクセル・シート、しかも、そのシートに、センサ機能／フィードバック機能なども付けてみた。そんな素材・材料が揃ってきたこともあるので、まずは、PID制御で（疑似三次元空間における）温度制御を行う例をいくつか作り、その後は、上記記事を参考にしつつ「（誤差を付加した）センサ→カルマンフィルタ→制御量最適化」という例でも作ってみることにしよう。
」など。