hirax.net::Keywords::「スペクトル」のブログ

■Spectrum Color Conversion　

　Spectrum Color Conversion は分光的な色変換を行うことができるWEBページです。 Spectrum Color Conversion::RGBtoCMY はディスプレイで用いられているような赤・緑・青のRGB加算混色で示された色（スペクトル）を、印刷などで用いられているシアン・マゼンダ・イエローのCMY減算混色で表現された色（スペクトル）へと変換します。その逆に、CMYからRGBへの変換を行うのが、Spectrum Color Conversion::CMYtoRGB です。各色に対する入力値は、RGBtoCMY・CMYtoRGBのいずれの場合も、0から255までの値を入れるようになっています。なお、CMYtoRGB の際のD65という欄には、255という数値が入っていますが、これは減算混色時にインクを照らす照明光の明るさです。この数値を変える必要は特にありませんが、もしも、この照明光D65の強度を変えたりしてみれば、その強度に応じて明るくなったり・暗くなったりすることは確認できると思います。

　CMY<=>RGB の色変換の際に用いている基準は、「スペクトル強度の差の自乗和が最小になること」です。つまり、人の視覚特性などに特化した色変換ではなく、単純に分光強度の形状が近くなるような色変換を行っています。また、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルは非常に大雑把な値を使っています。特に、シアン・マゼンダ・イエローに関しては、印刷で用いられているインクとは異なり、比較的理想に近い吸収スペクトルの場合を示しています。もしも、赤・緑・青、および、シアン・マゼンダ・イエローの各色のスペクトルを眺めてみたい場合には、RGBtoCMYやCMYtoRGBの入力値として、単色だけを255にして、それ以外の色を0にしてみて下さい。たとえばシアンだけがある場合の単色スペクトルを眺めたければ、シアン=255, マゼンダ=0、イエロー=0にする、という具合です。すると、その色だけを使った時のスペクトルを見ることができるわけです。ただし、減産混色の場合に表示されるのは、いわゆる吸収スペクトルではなく、インクに吸収されなかったスペクトルということになります。また、CMYが示している量には対数変換がかけられています。

　RGBtoCMYとCMYtoRGBは、相互に入力スペクトルと再現されたスペクトルを比較することもできますから、RGBとCMYの間で相互に色変換を繰り返しながらスペクトルの変化を眺めてみるのも面白いかもしれません。

　なお、このSpectrum Color Conversion は、離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージをWolfram Technology 社のMathematica上で作成し、webMathematica エンジンを用いることで、web アプリケーションとして動作しています。

• 分光画像処理入門
• 応用Mathematica

■「無名関数」と「吾輩は猫である」　

　夏目漱石の「吾輩は猫である」は、雑誌「ホトトギス」に1905年1月に発表された。最初は、冒頭の章だけで完結する短い読み切り小説だった。

　吾輩は猫である。名前はまだ無い。　…吾輩がこの家へ住み込んだ当時は、主人以外のものにははなはだ不人望であった。どこへ行っても跳ね付けられて相手にしてくれ手がなかった。いかに珍重されなかったかは、今日に至るまで名前さえつけてくれないのでもわかる。

　「吾輩は猫である」を連想したのは、Mathematicaの「純関数」の勉強のための練習題材を書いていたときだ。Mathematica の入門・中級の講習会に参加すると、この純関数とやらが登場した途端に、講師が話す内容を見失ってしまうことが多い。講師の筋道が見えなくなってしまう理由は、純関数の必要性・存在価値といったものが今ひとつわからないままに、純関数がいきなり登場してくるからである。もちろん、「（数値でなく）関数を引数として与える」ということに慣れていない生徒が多いこともあって、いつも、純関数が登場した瞬間に、何かその場が失速したような感覚を受ける。

　話の流れ・必然性がなくても、文法をただ暗記することができる人であれば、おそらく何の問題もないのだと思う。あるいは、他のプログラミング言語をよく知っていて、文法の必然性が自然と理解できる人たちであったなら、これもまた問題は起きないのだろうと思う。しかし、私も含めて、入門・中級の講習会に来ているような、そうでない多くの人たちの場合は、純関数が登場した途端に、話についていけなくなることが多いように感じるのである。

　Mathematica における純関数 "Pure Function" というのは名前(シンボル)を持たない関数で、ほかの関数への引数などとして、関数の内容を書いた一瞬だけ使われるものだ。もう少し違う呼び方をしてしまえば、つまりそれは「無名関数」だ。「無名」というところが重要で、名前がないから、使ったら最後もう二度と呼ぶ・使うことはできない、ということである。つまりは、「使い捨ての関数」だ。この「関数を使い捨てる」というところで、どうしても引っかかってしまう。値を入力するのであれば、あまり考えることなどせずに、数字キーを2・3回押せばすむ。だから、値に名前（シンボル）と付けずに、使い捨てにすることには慣れている。けれど、関数を書く場合には、（ハッカーでない私たちは）頭も多少使わざるをえない。すると、せっかく考えて・苦労して書いたのだから、名前をつけて、あとで呼んでまた使うことができるようにしたい、などと思ってしまうのである。使い捨ての「無名」ということと、苦労をともなう「関数」ということを、なかなか重ね合わせることができないのである。

　そこで、自分なりの「純関数の存在価値・意義」を作ることで、その存在意義を納得したくて、純関数を使った例題を作ってみた。実は、それが前回の Spectrum Color Conversion を動かしているベース部分、「離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージ」である。これは、無名関数（純関数）を使うための例題である。このパッケージを使うと、スペクトルを描くのに、

plotSpector[ (128 red[#] + 255 blue[#])& ];

(128 red[#] + 255 blue[#])&

rgb=fitSpector[(D65[#]-128 cyan[#])&,red,green,blue]

　こんな例題を作ることで、無名関数アレルギーが低減した、と言いたいところなのだけれど、関数を使い捨てることには、やはりまだ慣れることができそうにない。関数を引数として渡すことは自然に感じられるようになっても、無名関数に名前をつけて、再度その関数を呼んでみたい気持ちはなかなか止められそうにない。名前をつけるより、その関数の中身をそのまま書いた方がわかりやすいとわかっていても、単純な名前をつけてしまいたくなる欲望はなかなか止められそうにない。

　その理由を考えてみると、やはり、苦労をともなう「関数」を使い捨ての「無名」にしてしまう、ということに一因がある。そして、もう一つ、名前をつけることで、単純化して安心してしまいたくなる、ということがあるように思う。ほんの何文字かの関数であっても、その内容を自分の頭で考えるよりは、なにがしかの単純な言葉で表現された関数名を聞いて納得したくなることがあるように思う。

　「吾輩は猫である」の第一章の最後、つまり、当初の読み切り短編小説「吾輩は猫である」はこのように結ばれる。

　吾輩は御馳走も食わないから別段 肥りもしないが、まずまず健康でびっこにもならずにその日その日を暮している。鼠は決して取らない。おさんは未だに嫌いである。名前はまだつけてくれないが、欲をいっても際限がないから生涯この教師の家で無名の猫で終るつもりだ。

■「研究者」と「経営者」　

　東京理科大学の宮原教授の講演を聞いた。それは、とても惹きつけられた講演だった。面白いと感じたポイントは２つあち、その一つめは、講演冒頭に「カルチャーショック」と題したスライドを見せながら話された内容だった。

　それは、「研究者」と「経営者」の間の「違い」である。話を聞きながら、走り書きしたメモをタイプしてみると、

• 研究者（理系）
• 誰も知らない新しいことを見つけ、新しいものを作り出す
• 帰納的推論をする
• これしかない
• 経営者（文系）
• 誰でも知ることのできることの関係性から新しい視点を作り出す
• 演繹的推論をする
• 色々あるさ
という具合になる。そして、講演をする時には、研究者は「たくさんのスライドを作りたがる」というし、経営者は「１つの言葉・スライドだけからでも、たくさんしゃべる」という違いがある、という。聞き間違い・書き取り間違いは多々ありそうだけれど、こんな感じの内容だった。

　もしも、研究者と経営者の間に技術者がいるのなら、上に書いた２つの中間になりそうだ。

　そして、もう二つ目の面白かった内容は、期せずしてポスターセッションと趣向が重なり、同じように「エイク・フェルメール・モネ・デカルト・ニュートン…」という名前が登場する歴史とスペクトルと絵画に関することだ。多分、こういった内容はある種鏡のようなもので、見る視点の深さに応じて内容の深さが変わるものだと思う。深く眺めようとすれば、どこまでも深い内容が隠されているし、浅く眺めようとすれば浅い内容しか目に入らない。そういったものだと思う。

この記事の「関連お勧め記事」を読む  >> 
キーワード(ブログ):研究|経営|イノベーション|理系|文系|エイク|フェルメール|モネ|デカルト|ニュートン|カルチャー|スペクトル|歴史|技術者|研究者

■光スペクトル操作用のMathematicaライブラリ　

以前、Mathematicaの演習用に作った「スペクトル操作用Mathematicaライブラリ」を少し直したので、ここ（”ColorLib_amature.nb”に置いておきます。以前作ったものと同じく、スペクトル・データをリストのような離散データではなくて、関数として（純関数＝無名関数として、あるいは、明示的な関数として）取り扱うという点が特徴だと思います。「（せっかくMathematicaで解くのですから）解析的に解く」「使用者には離散化・数値計算など、面倒くさい汚い部分は見せない・見たくない」という方針で作ったものです。

以前のものからの変更点としては、"spectorPlot"や"labPlot""labColorPlot"など、関数名のMathematicaの命名規則に合わせた変更、加法混色・減法混色用関数の追加・グラフ表示関数の追加・バグ修正といったところです。

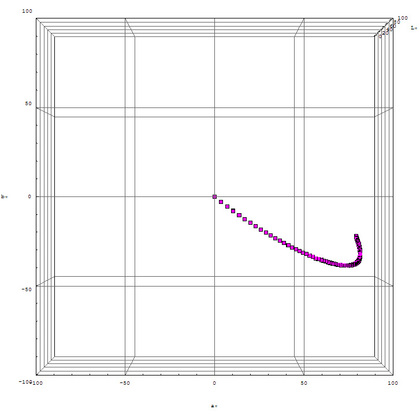　最初のラフスケッチが、絵画の原理を自分なりにおさらいするためのものだったので、濃度変調・面積変調などを扱おうとする場合には、比較的簡単に・気持ち良く作業ができると思います。たとえば、下記のようなコードを書けば、D65光源のもとで、赤紫色の絵具を重ね塗りしていったときの色の具合を CIE Lab 空間で眺めたりすることができます。

labPlot[
　Map[lab,
　　Table[transmissionSpector[D65,
magentaFilter, d],{d,0,10.0,0.1}]
]
];

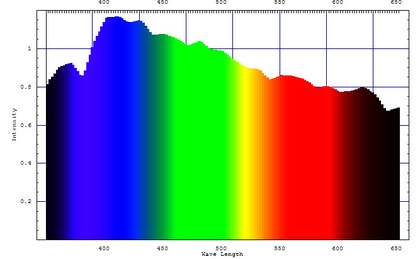　また、白色光照射時に黄色い絵具を塗り拡げる面積を増やしていった場合の反射光スペクトル変化をアニメーションとして作成・グラフ表示するコードはこんな感じです。"addtiveMixtureSpector"は加法混色用の関数で、"transmissionSpector"は減法混色用の関数です。お遊びソフトですが、色々遊ぶこともできるかもしれません。

Map[spectorPlot,
Table[
addtiveMixtureSpector[
{whiteLight,
transmissionSpector[whiteLight, yellowFilter, 1]},
{1-r, r} ],{r,0,1,0.1}]];

■「スペクトル操作Mathematicaライブラリ」で動画を作る　

　光スペクトル操作用のMathematicaライブラリで、スペクトル変化の動画を作ると、こんな感じになります。Map　も　spectorPlot　も　Table も addtiveMixtureSpector　も whiteLight も cyanFilter も・・・どれも「関数」です。addtiveMixtureSpector　や whiteLight や cyanFilter は「関数を返す関数」で、Map などは関数を引数にとる関数です。Mathematica でコードを書いていると、なぜか自然に関数を重ね合わせていくような書き方が気持良くなってきます。

Map[spectorPlot,
　Table[
　　addtiveMixtureSpector[
　　　{whiteLight,
　　　transmissionSpector[whiteLight,
　　　cyanFilter, 1.0]}, {1-r,r}]
　,{r,0,3,0.05}]]

　それで、今この瞬間の悩みはMathematicaで"spectorFitting[targetSpector_,usingSpectrum]"というような関数をどうやって書くか、ということです。targetSpector は、任意のスペクトルを表現する関数で、usingSpectrum は「スペクトルを表す関数群」で要素数は任意のリストです。usingSpectrumを使いtargetSpectorをどのように表現するかを、最小二乗近似で最適解をNMinimize で解くというのが、そんな関数を作るときの定番の手順なのだろうと思います。つまり、方程式と制約条件を動的に作成し、それをNMinimize で解いた結果を返す、という具合です。