1999-09-08[n年前へ]
■続ACIIアートの秘密 
階調変換 その1
さて、今回は
の続きである。今回はASCIIアートの階調変換に関する話である。原画像からASCII文字画像に変換するときにどう変換するか、という話の第一話である。 まずは、白から黒までの256階調の基準チャートとASCII文字によるチャートを示してみよう。
両者ともかなり縮小表示している。従って、ASCII文字チャートの方は文字がつぶれて滑らかに見えている。一見すると、ASCII文字チャートの方は白地に黒い文字を印字しているため、完全に黒いようなものは出力できない。そのため、全体的に白く見える。
これらの2つの画像のヒストグラムを示してみよう。ばらつきが多少あるが、256階調の基準チャート(上)では256階調にわたって存在している。しかし、ASCII文字チャート(下)では(ざっと見た限りでは)35階調程度しか存在していない(これは使用するフォントによって異なる)。もともと、ASCII文字は数多くあるわけではないし、平均濃度が等しい文字も存在するので、この程度になってしまうのはしょうがない。また、最も黒い領域でも、256階調の基準チャート(上)の半分程度の濃度しかない(これも使用するフォントによって異なる)。
ところどころに「使用するフォントによって異なる」という注釈を入れいるがこれが前回作成したimage2asciiの特徴である。指定のフォントを用いて画像出力を行った結果を用いてガンマテーブルを再構成するのである。逆にいえば、その指定のフォントを用いない場合には意図した画像は得られないわけである。「DeviceDepend」な技術というわけである。
 |
 |
そもそも、オリジナルの画像から、この程度の階調しかないASCII文字画像へどのように変換したら良いだろうか? 先に基準チャート(上)とASCII文字チャートの例を示したが、そもそもそのASCII文字チャートはどのようにして変換するのだろうか?
まず思いつくのはオリジナル画像の濃度に一番近い濃度の出力を行う方法である。それを濃度精度重視の変換と呼ぼう。そして、もうひとつは、オリジナル画像の中での相対濃度を基準とする変換である。すなわち、オリジナルの最大濃度をASCII文字出力による最大画像に合わせ、オリジナルの最小濃度をASCII文字出力による最小画像に合わせ、あとは単に線形に変換する方法である。こちらを(まずは単純な)階調性重視の変換と呼ぼう。その変換の構造を以下に示してみる。
 |  |
濃度精度重視の変換(左)では、ある濃度以上になると全て同じ濃度で示されてしまう。階調性重視の変換(右)ではそんなことは生じない。しかし、オリジナルの画像と変換後の画像の濃度はかなり異なってしまう。これら2つのやり方によるASCII文字チャートをそれぞれ示してみる。
濃度精度重視によるASCII文字チャートと階調性重視によるASCII文字チャート(下)のどちらが自然だろうか?濃度精度重視によるASCII文字チャートは階調の中程までは基準チャート(上)と非常に近い濃度を保っている。そのかわり、それ以降の濃度が高い部分はまったく階調性を失っている。少なくともこの基準チャート(上)のように256階調にわたり均等に濃度が存在するような画像を扱うのであれば、階調性重視によるASCII文字チャート(下)の方が自然だろう。というわけで、前回作成したimage2asciiは階調性重視による変換を用いている。
さて、今回は256階調全てにわたって滑らかな基準チャートを用いて考えてみた。しかし、実際の写真はそんなものではない。色々な濃度が均等に現れるわけではないし、そもそも狭い濃度領域しかない画像の場合もあるそういった場合には、数多くの問題が生じる。また、単に(単純な)階調性重視によるASCII文字チャート(下)が優れているわけでもなくなる。場合によって何が優れているかは異なるのだ。一般的な画像において、一体どんな問題が生じるのか、ということを次回に考えてみることにする。そして、新たに2種類の変換方法を加えてバージョンアップしたimage2asciiの登場するわけである。
今回は、その3つの変換方法の違いにより出力画像にどのような違いが生じるかを示すだけにしておく。先入観が無い状態で、優劣を判断してみると良いと思う。次の例は人物写真である。まずは、オリジナルの写真である。
 |
以下にimage2asciiを用いて変換したものを示す。
 |  |  |
これらの違いがどのようなものであるかを次回に考える。
1999-10-15[n年前へ]
■続々ACIIアートの秘密 
階調変換 その2
前々回の
の時にASCIIアートに関する情報を探した- 清竹's テキスト絵 HPリンク集 (http://www2.nkansai.ne.jp/users/kiyo/ )
「限られた出力階調を有効に利用するため、画像の濃度ヒストグラムの補正を行ないます。1パス目で、濃度ヒストグラムをカウントし、そこからヒストグラムが平坦になるような濃度変換関数を生成します。(ヒストグラムを平坦にするのは、情報のエントロピーをなるべく保存するためです。)」とある。Q02TEXTはimage2asciiと同様のテキストアート作成プログラムである。前回のの最後で(3).情報量を最大にするモデル というのを導入したが、これがそのエントロピー最大化アルゴリズムに近いものを導入してみたものである。何しろ、この考えを使っていくのは乏しい階調性の出力機器には非常に有効なのだ。今回は、この「エントロピー最大化アルゴリズム」について考えてみたい。
Q02TEXTは「 .:|/(%YVO8D@0#$」の16階調を使用するテキストアート作成プログラムである。それに対して、「ASCIIアートの秘密」で作成したimage2asciiが使用可能な階調数は一定ではない。指定されたフォントを一旦出力してみて、その結果を計測することにより、出力可能な階調数を決定している。したがって、指定したフォントでしか階調の確かさは保証されない。その代わりに、指定されたフォントを使えば割に豊かな階調性を使用できることになる。
また、得られる階調は一般的に滑らかではないので、Q02TEXTが使っているアルゴリズムとは少し違うものを導入している。
通常ASCIIアートは色々な環境で見ることができるのがメリットの一つである。しかし、image2asciiはフォントを限定してしまっている。これは、目的が通常のASCIIアートとは異なるからである。私がimage2asciiを作った目的は、それを仮想的な出力デバイスとしてみたいからである。その出力で生じる様々な問題を調べたり、解決してみたいのである。
さて、前回の最後に示した3種類の画像変換は
- 単純な階調重視モデル
- オリジナルの0を出力画像の最小値に
- オリジナルの255を出力画像の最大値にする
- 拡大した単純な階調重視モデル
- オリジナルの最小値を出力画像の最小値に
- オリジナルの最大値を出力画像の最大値にする
- 情報量を最大にするモデル
- エントロピーを最大にするための階調変換を行う
これら3つの変換方法の違いにより出力画像にどのような違いが生じていたかを、まずはもう一度見てみる。まずは、オリジナル画像である。これは、「私の尊敬する」S大先生である。私は尊敬とともに「ロボコップSさん」あるいは、「ロボSさん」と呼ぶのだ。いや、本当に。
 |
以下にオリジナル画像及びimage2asciiを用いて変換したものを示す。
 |  |  |  |
- (1).単純な階調重視モデルが比較的白い個所では一番オリジナルに忠実な濃度であることはわかるだろう。ただし、黒い部分に関しての表現力は極めて低い。
- (2).階調性を少しだけ改善したものではそれより視認性が改善している。
- (3).視認度の高い画像ではあるが、オリジナルとは濃度などは異なる?
それでは、これらの画像のヒストグラムを調べてみる。先の「(ヒストグラムを平坦にするのは、情報のエントロピーをなるべく保存するためです。)」というのとの関係を調べたいわけである。
 |  |  |  |
ASCII ARTには濃度の表現領域には限度がある。そのため、(1),(2),(3)はいずれも濃度が最大を示す個所でもオリジナルよりかなり濃度が低い。また、(1),(2)はオリジナルとヒストグラムの形状も少しは「似ている」が、(3)においては、かなり異なっているのがわかると思う。(3)はヒストグラムの形状はかなり異なるにも関わらず、視認度は高くなっている。これが、エントロピーを最大化(すなわち情報量を最大化)しているおかげである。ヒストグラムがかなり平坦になっているのがわかるだろう。
というならば、エントロピーの計算もしなければならないだろう。もちろんエントロピーと言えば、
でも登場している。「エントロピーは増大するのみ...」というフレーズで有名なアレである。情報量を示す値だといっても良いだろう。せっかく、「ハードディスク...」の回で計算をしたのだから、今回もその計算を流用してエントロピーを計算してみたい。といっても、無記憶情報源(Zero-memorySource)モデルに基づけば、ヒストグラムが平坦すなわち各濃度の出現確率が等確率に近いほどエントロピーは高いのが当たり前であるが... この前作成したMathematicaのNotebookを流用するために、オリジナルと3つの変換画像を合体させる。そして、そのヒストグラムを見てみよう。このヒストグラムが非常にわかりにくいと思うので、一応説明しておく。あるY軸の値で水平に1ライン抽出して、その部分のヒストグラムを右のグラフに示しているのである。
 |  |
例えば、オリジナルの画像では髪の毛がある辺り(Y軸で10から30位)では、ヒストグラムを見ればレベルが50位の黒い所が多いところがわかる。それに対して、変換後の画像では、一番濃度の高い所でも150前後であることがわかるだろう。
それでは、それぞれ、Y軸でスライスしてその断面におけるエントロピーを計算したものを次に示してみる。
 |  |
本来は、画像全面におけるエントロピーを計算するのが、望ましい。しかし、ここで使っているような、Y軸でスライスしてその断面におけるエントロピーでも、オリジナルの画像が一番エントロピーが高く、(3)の変換画像(つまり一番上)のものが次にエントロピーが高いのがわかると思う。つまり、情報量が高いのである。
エントロピー量とあなたの感じる「視認度」とが相関があるかどうかは非常に興味があるところだ(私にとって)。エントロピーが多くても(すなわち情報量が多くても)オレはちっともいいと思わないよ、とか、おれは断然エントロピー派だね、とか色々な意見があったらぜひ私まで教えてほしい。
「お遊び」に見えるASCIIアートも、調べていくと実は奥が深いのだなぁ、とつくづく思う。といっても、もちろん本WEBはお遊びである。なかなか、奥までは辿りつかない(し、辿りつけない)と思うが、この「ASCIIアートの秘密」シリーズはまだまだ続くのである。
1999-11-20[n年前へ]
■バナー画像のエントロピー 
がんばれ、JPEG
前回、
で「バナー画像中の文字数とファイルサイズ」に注目し、「文字情報密度」というものについて考えてみた。情報密度を考えるのならば、で考えたエントロピーについても計算してみなければならないだろう。そこで、今回は前回登場したバナー画像達のエントロピーを計算してみることにした。それにより、情報圧縮度について考えてみることにするのだ。
そうそう、今回も「本ページは(変な解説付きの)リンクページであります」ということにしておく。他WEBのバナー画像を沢山貼っているが、それはこのページが「リンクページ」であるからだ。
エントロピーを計算し、画像の圧縮度を調べる際に、今回はファイル先頭の400Byteにのみ注目した。ファイル全体で計算するのは面倒だったからである。各バナー画像でファイルサイズが異なるからだ。そこで、全て先頭400Byteに揃えてみた。
行う作業は以下のようになる。
まずは、画像ファイルの「先頭400Byteの可視化画像」を作成する。これは、各ファイル中の各Byteが8bitグレイ画像であると考えて、可視化したものである。以前書いたように、「てんでばらばらに見えるものは冗長性が低く、逆に同じ色が続くようなものは冗長性が高い」のである。もし、同じ色が続くとしたならば、「また、この色かい。どうせ、次もこの色なんだろ。」となってしまう。次の色の想像がつく、ということはすなわち、情報としては新鮮みのないものとなる。つまり、情報量が少ないのである。その逆に、情報量の多いものは、てんでばらばらで次の色(データ)の予想がつきづらいもの、となるわけである。まずは、そのてんでばらばら具合を「先頭400Byteの可視化画像」で確認する。
次に、てんでばらばら具合をヒストグラムで確認する。各Byteが0から255のどの値をとることが多いかを調べるのである。てんでばらばらであれば、どの値をとる確率もほぼ同じであり、フラットなヒストグラムになるはずである。逆に、ヒストグラム上である値に偏っていれば、値の予想がつきやすく、情報量が少ないということになるわけだ。
最後に、各Byteのデータを「8元無記憶情報源モデル」に基づいて計算したエントロピーを計算した。各Byteのエントロピー、すなわち、平均情報量は最大で8となる。当たり前である。1Byteは8bitであるから、最大限有効に使いきれば、情報量は8bitになる。
それでは、青い「hirax.net できるかな?」バナーを例にして見てみる。
| 文字情報密度 | ファイルサイズ(Bytes) | 画像 | 先頭800Byteの可視化画像 | ヒストグラム | エントロピー(bits/Byte) |
| 35 | 662 |  |  | 7.1 |
この画像ファイルはトータルで662Bytesであるが、その先頭400Bytesの可視化画像はけっこうばらばらである。それは、ヒストグラムをみても確認できる。少し、0近傍が突出しているが、それを除けば、かなり均等である。そして、エントロピー、すなわち、1Byte当たりの情報量は7.1bitである。満点で8bitであるから、7.1bitはなかなかのモノだろう。
それでは、前回登場したバナー画像達に、同じ作業をかけてみる。
| 文字情報密度 | ファイルサイズ(Bytes) | 画像 | 先頭400Byteの可視化画像 | ヒストグラム | エントロピー(bits/Byte) |
| 31 | 874 |  |  | 6.7 | |
| 34 | 648 |  |  | 7.2 | |
| 35 | 662 |  |  | 7.1 | |
| 40 | 763 |  | 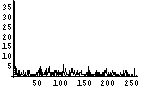 | 7.1 | |
| 44 | 1003 |  |  | 7.1 | |
| 54 | 750 |  | 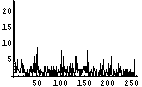 | 7.1 | |
| 58 | 864 |  |  | 6.6 | |
| 112 | 2472 |  |  | 3.8 | |
| 124 | 2348 |  |  | 7.0 | |
| 155 | 465 |  |  | 7.3 | |
| 223 | 3116 |  |  | 7.0 | |
| 294 | 881 |  | 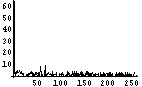 | 6.6 |
IntenetExplorer、RealPlayerといった、ヒストグラム上で突出している値がある画像はエントロピーが少ない。すなわち、平均情報量が少ない。大体、6bit台である。gooは0近傍の値が突出しているのが足を引っ張り、6.6bitとなっている。これらは、1Byteの8bit中の1bit強が無駄となっているわけである。
最高点はMacの7.3bitである。8bit中で7.3bitの情報量を持っているのである。逆に言えば、0.7bitは無駄ということになる。しかし、8bit中7.3bit使い切っているのはなかなかのものである。
それ以外は大体7bit台で拮抗している。しかし、それはいずれもGIF画像である。そう、唯一のJPEG画像である「今日の必ずトクする一言」が3.8bitと低い情報量であるのだ。しかし、これには、いろいろな理由があると思われる。例えば、ファイル全体ではなく先頭のみを見ているため、JPEGのヘッダー部分が入ってしまい、冗長性が高くなってしまっている、とかである。全体でなく、部分で評価しているのは非常にマズイだろう。また、GIFが情報圧縮していることもあるだろう。そのため、JPEG陣営にはかなり不利であったと思われる。
そうそう、今回は情報圧縮度にだけ注目したから、JPEGに不利な結果になった。けれど、他のいろいろな理由を挙げれば、GIFは使いたくないという気持ちもあるのだけれどね。けど、便利なんだよね。
2000-02-24[n年前へ]
■「モナリザ」の自己相似形 
48x48の「世界への微笑」
以前、
で、ASCII文字で描かれたモナリザを初めて見たのは、まだ大型コンピューターしかなかった頃だ。当時、記憶媒体の紙テープをパンチした紙くずと、ラインプリンタから出力されたASCIIアートで遊んでいた。と書いた。
私がモナリザを見たのはこのASCIIアートのモナリザが初めてだった。何故か住宅の天井裏にASCIIアートをモチーフにしたカレンダーが貼られていた。天井裏に貼られたモナリザはとても趣があった、と思う。
そういうわけで、初めて見たモナリザは、カラーではなくて白黒の、しかもASCIIアートのモナリザだったのである。
もちろん、そのモナリザはもうどこにもいない。そこで、
の時にバージョンのIMAGE2ASCIIでモナリザをASCIIアートに変換したのが下の画像だ。 |
こんなに縮小してしまうと、ASCIIアートに見えない。そこで、顔(特に目)の辺りの部分の拡大図を下に示してみる。
 |
こうしてみると、ASCII文字であることはわかる。しかし、全体像は全く見えなくなる。「これが、モナリザの目の辺りだ」と言っても全く信用されないことだろう。
こういう画像を考えるときは、全体像と拡大図の両方を感じなければいけない。拡大図しか感じられないと、「木を見て森を見ない」状態になる。そして、全体像しか見ない場合には「実際の所をなにも知らない」状態になる。
さて話を戻す。私が眺めていたASCIIアートをのモナリザを初めとして、モナリザほど「本歌取り」の「本歌」に使われているものもない。「モナリザの微笑」からは、沢山の人が色々なものを引き出してきた。「モナリザ」の微笑はどうにも奥深く見えるから不思議である。その微笑の先に何があるのかを深く考えさせる。その答えはなかなか見つけられない。
そういうわけで、東京都美術館で開催されていた「モナリザ100の微笑」を先日見に行ってきた。
特に、私が見たかったのはこれである。福田繁雄の「世界への微笑」だ。
 |
もう、おわかりだと思うが、これは切手によるコラージュである。このモナリザの顔(特に目)の辺りの部分の拡大図を次に示してみる。
 |
拡大すると、全体像が全く判らなくなるというところは、ASCIIアートと全く同じである。こういった、離れてみると、やっと何が描かれているかわかる、という画像はとても面白い。
そこで、今回はそういう画像を作成してみたい。つまり、「小さな画像の集合が集まって一つの画像になる」ようなものだ。
それに加えて、先ほど
「モナリザ」の微笑はどうにも奥深く見えるから不思議である。と書いた。「モナリザの微笑」を眺め考えると、その先には結局「モナリザ」しか見えてこない。答えが見えないのである
まるで、それはタマネギのようで、自己相似形という言葉さえ思い起こさせる。
そういうわけで、小さな「モナリザ」が集まって一つの「モナリザ」となるような画像を作成してみることにした。逆に言えば- 「モナリザ」を見つめていくと、その先にさらに小さな「モナリザ」が見えてくる- という画像である。
そういう画像を作るために、簡単なアプリケーションを作成してみた。それが、これである。
名前はjoconde.exeだ。画像を読み込み、その画像をその画像自身の縮小画像(48x48個)で表現するのである。福田繁雄は切手や国旗で「モナリザ」を表現した。私は48x48個の「モナリザ」で、さらなる「モナリザ」を表現するのである。いつものごとく、色々な画像のフォーマット対応のためにはSusieプラグインを必要とする。もちろん、言うまでもないと思うが信用度はアルファ版以下である。
さて、作成した画像 - 題して、48x48の「モナリザ」 -を次に示そう。「モナリザ」の微笑は「モナリザ」でしか表現し得ない、という私の気持ちの表れである。この画像をクリックすれば、元のサイズの- 48x48の「モナリザ」 - を見ることができる。
 |
この画像では、48x48個の「モナリザ」でできていることはわかりづらい。そこで、上の画像のモナリザの目の辺りを拡大したものが以下である。
 |
この - 48x48の「モナリザ」 - を眺めていると、「モナリザ」の微笑について色々と考えてしまう。どこが、一体魅力となっているのだろうか? いくら考えてみても、よくわからない。
さて、モナリザと言うと、夏目漱石と「モナリサ」にも言及しなければならないだろう。しかし、それは次回のココロだ。