2000-01-27[n年前へ]
■「富士の樹海」を目指せ 
磁界を可視化しよう
以前から探していた「面白いもの」を入手した。この写真がその「面白いもの」なのであるが、何だかわかるだろうか? ちなみに、大きさは「1cm×5cm」位のシートである。
 |
これは「マグネビュアー」というものである。磁界を可視化してくれるシートだ。マイラーフィルムの間に磁性体を混入させたマイクロカプセルを入れることで、磁界に対する配向性を持たせたものだ。と、言葉でいってもなかなかわかりにくいので、磁界を可視化した写真を示してみる。何しろ、百聞は一見に如かずである。
次の写真は某ピザ店のマグネットシート(よく冷蔵庫の扉に張り付ける奴)の上に「マグネビュアー」をのせたところである。ピザ屋は私の食生活を支えていると言っても良い。私が生きているのはピザ屋のおかげである。
 |
私の「命の恩人」でもある某ピザ店のマグネットシートがつくる磁界が見て取れるだろう。磁界が可視化されているのである。
本WEBではこれまで様々な「可視化」で遊んできた。例えば、
- 感温液晶でNotePCの発熱分布を可視化する
- ハードディスクのエントロピーは増大するか?- デフラグと突然変異の共通点 - (1999.03.28)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- 恋の力学 -恋の無限摂動 - (1999.12.21)
- WEBサイトの絆 - WEBの世界を可視化しよう- (2000.01.13)
- 夜のバットマン - 超音波を可視化しよう- (2000.01.17)
上に示した「某ピザ店のマグネットシートの表面」の磁界の様子も面白いが、もっと面白いのは「某ピザ店のマグネットシートの境界」の磁界を可視化したものである。
それが下の写真である。磁界の様子が実感できるのではないだろうか?
 |
下に示す図はドーナツ型の磁石の周りの磁界をCUPSを用いてシミュレーション計算した結果である。この計算結果と同じようなものが「マグネビュアー」を使うと簡単に可視化できる。
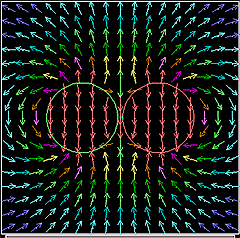 |
普通、こういった磁界の可視化は磁気造影剤や砂鉄みたいな磁性体粒子を用いるのであるが、そういったものはどうにもハンドリング性にかける。液体や粉体などを家の中で実験に使うのはイヤである。いや、もちろん仕事で使うのもイヤであるが... そこで、この「マグネビュアー」が登場するわけだ。
それでは、その他の面白そうな磁界を可視化してみたい。磁界と言えば、やはりアレの登場だろう。もちろん、アレと言えば磁気カードである。クレジットカードや銀行のキャッシュカードといった磁気カードだ。一例を次に示してみる。こんなヤツだ。
 |
カードの下に黒い磁気データ記録部があるのがわかるだろう。
それでは、その「磁気データ記録部」に「マグネビュアー」をのせてみよう。はたして、磁気データは可視化されるだろうか?
 |
といっても、この写真ではわかりにくいので、「マグネビュアー」を拡大してみよう。すると、バーコードのような模様が見えるのがわかると思う。「磁気データ」が簡単に可視化されているわけである。この「マグネビュアー」と普通のスキャナーがあれば磁気データ読み取り機がなくても磁気データが読みとれるのである。
 |
しかし、このカードに関しては内容を解析するとマズイ事情があるので、次回に「ソフマップ」のカードを題材にして磁気カードの内容を可視化してみるつもりだ。題して、
- ソフマップでお買い物 - 磁界の可視化とバーコード - (仮称)
さて、話は変わるが、私はこの「マグネビュアー」を手に「富士の樹海」を目指すつもりだ。「富士の樹海」では」方位磁針が変な方向を示すと伝えられている。そしてまた「富士の麓」ではとかく人は判断を誤りやすいとも聞く。船頭多くして船山に登ると言うが、「富士の樹海」には判断を誤った船が沈没しまくりである。
私は「富士の樹海」の真実をこの「マグネビュアー」で明らかにするつもりだ。「富士の樹海」の謎を明らかにするのである。何故、方位がそして人が判断を誤るのか、その謎を明らかにするのだ。
しかし、もしも、もしも、の話であるが、本WEBの更新が止まった際には、「富士の樹海」で私が眠っていると思って欲しい。「マグネビュアー」が役に立たないはずがないのだが、きっと何か判断を間違えたのであろう。そうそう、あくまで「富士の樹海」である。「富士の裾野」ではないので念のため...
2000-02-05[n年前へ]
■恋の固体物理学 前書き編 
シリコン・エイジの恋
これまで、様々な「恋の形」について考えてきた。古くは、
であったり、あるいは、であったりした。最近の「恋の力学」シリーズでは、初めに男と女の間の「恋の二体問題」を考え、そして二人の男と一人の女の間の「恋の三体問題」を考えてきた。しかし、それらの「恋の力学」が取り扱ってきたものは、ごく少数の登場人物により演じられる物語を解析したものである。また、特に「男」と「女」の間に性質的な差がないものとして、解析を行ってきた。
このような解析の前提条件、
- ごく少数の登場人物
- 「男」と「女」の間に性質的な差がない
- 数え切れない多数の人物が登場し
- 「男」と「女」の性質の間に差がある
例えば、
- 「男」も「女」も結構人数はいるのであるが、その数がかなり違う。
- 「男」が諸星あたるのように、やたら行動力があるが、「女」の方ははなかなか動かない
- 恋人達に何かのショックを与えると分かれてしまう。
- その場の雰囲気でカップルになっちゃった
こういった色々なことが「恋の物理学」では起きる。しかし、
で書いたように、夏目漱石の時代に作り上げられた「恋の力学」ではそのような現象の解明は困難である。そこで、新たな「恋の科学」の分野を作り上げ、そういうことについて考えを巡らせていきたい、と思う。とはいえ、いきなりやるのは私には難しい。そこで、まずは解析のための準備をしていきたい。
というわけで、本シリーズは題して、「恋の固体物理学」である。先に述べたような「不均等な恋の挙動」を例えば半導体工学のような固体物理学のテクニックを用いて解明したいと思うのだ。割に単純な「恋の力学」シリーズとは別に、「恋の固体物理学」シリーズを始めたいと思うのである。
普通に考えるならば、 - 何故「恋」の挙動解明に、半導体工学? - と思われるかもしれない。確かに、唐突であるとは思う。しかし、考えてみればそれほど不自然ではない。何しろ、現在はシリコンの時代であると言われる。
プラスティック・エイジを経て、現在はシリコン・エイジが世界を支配している。シリコン= 半導体技術により、世界は動いているのだ。そうであるなら、「恋に動かされる人」の挙動も、、半導体技術を用いることにより解き明かすことができるかもしれない。(いや、もちろん今考えた理屈である。簡単に言えば、こじつけである。)
そしてまた、「恋」は一般的に(例外はあるが)
- 男
- 女
- プラスの「正孔(ホール)」
- マイナスの「電子(エレクトロン)」
- 「男」も「女」も人数はいるが、その数がかなり違う。
そのような理屈で半導体工学と関連づけながら、「恋の固体物理学」について考えてみたいと思う。
このシリーズは少しヘビー(私にとって)なので、今回は前書きのみに留めたい。これから公開予定の作品群を紹介すると、
- 恋の固体物理学 恋のバンドギャップ編 - 彼女の防護壁を突破しろ! - (仮称)
- 恋の固体物理学 恋のドーピング編 - 女子校の教師はパラダイスか? - (仮称)
- 恋の固体物理学 恋の熱励起編 - 別れたくなかったら頭を冷やせ - (仮称)
- 恋の固体物理学 恋のp-n接合編 - 一方通行の恋の行方 - (仮称)
- 恋の固体物理学 恋のEinsteinの関係式編 - 本気と浮気の境界線 - (仮称)
まだまだ続く「恋の力学」シリーズと共に「恋の科学」を作り上げていきたいと思う。
2000-02-13[n年前へ]
■競馬の写真判定とパノラマ写真 
パノラマ写真と画像処理 Part.2
前回 、
の時にi_matさんから頂いたメールを紹介した。i_matさんは- I*MAT The HomePage (http://www.nsknet.or.jp/~i_mat/ )
- atoz@gol.com (http://www2.gol.com/users/atoz/index.html )
さて、前回
これらのソフトのStack-Slice機能を用いれば「複数画像(動画)からの走査線抽出」ができる。その使用例と、その面白い座標軸変換について考えてみたい。と書いた。今回もまた「数日後には登場」と言った割には時間が経っているような気もする。しかし、ここのところ文字通り忙殺されていたのである。と、言い訳をしながら今回この作業をやってみることにした。しかし、このページは少々重くなってきた。まして、走査線の抽出の話は使用画像が多くならざるをえない。そこで、次回、詳しく使用例を紹介することにする。
よく、次回登場と言ったまま数ヶ月経つことがあるが、今回は大丈夫である。少なくとも数日後には登場することと思う(多分)。
まずは、
- 「複数画像(動画)からの走査線抽出」
- 「座標軸変換」
以下に示す連続の画像は競馬のゴール地点に競走馬が到着した瞬間である。「馬に見えない」という人がいたら、それは目がおかしい。誰がなんと言おうとこれは馬である。馬と鹿の区別がつかない人は馬鹿と呼ばれるが、これはとにかく馬なのである。
 視野の中に馬がもっと入ってくる。
視野の中に馬がものすごく入ってる。 |
さて、このビデオカメラで撮影された画像は例えば以下のようなものである。
 |
撮影された各時間の画像から、この画像の赤で囲んだところを抽出し、並べたらどのようになるだろうか?
それはこのようになるだろう。よくある競馬の着順判定写真である。
 |
一見、これまで眺めてきたビデオカメラで撮影された画像と同じように見えるが、全く違う。ビデオカメラの撮影画像の動画中における、複数画像間の「位置」は全く変化していない。変化しているのは「時間」だけである。
だから、このような赤い長方形の画像を並べた方向というものは「時間軸」を意味しているのである。それを、下の画像に示してみる。
 |
この画像は縦方向は「空間軸」であるが、横方向は「時間軸」なのである。ビデオカメラの画像が縦横共に「空間軸」を示しているのに対し、その一軸を「空間軸」から「時間軸」に変換したものなのである
この競馬の着順判定写真の場合、カメラは空間に固定され「時間軸に変化するもの」を撮影していた。だから、このように各画像から一部を抽出して並べると、それは「時間軸」に対する変化を示すものを得ることができる。
また、例えば実験条件を変えたときの計測画像に対して「各画像から一部を抽出して並べる」ということをするならば、それは「空間軸」x「実験条件」というものを表す画像を得ることができる。
それでは、時間的には変化しないものを、ビデオカメラで撮影する方向を変化させながら撮影したらどうなるだろうか?例えば、ビデオカメラを下のようにして360度回転させながら撮影をしてみるのである。
 |
この場合撮影画像の各画像は撮影方向角度が異なるわけである。従って、先ほどのように一部分を抽出して並べると、一方向は「空間軸」であり、もう片方の軸は「撮影方向角度」になる。結局当たり前ではあるが、ある位置から眺めた周りの景色が得られるわけだ。
これが、前回i_matさんの要望していた
- 8ミリビデオを横倒しにして、 モーター回転するヘッドでぐるりと360度撮影し、
- その撮影した動画ファイルの、各フレームから走査線にして数本分を抽出し(インターレースで256本のうちセンター128本目の前後数本の走査線分)、
- それを貯めて1枚のjpgファイルにする、
- そのJPEG画像をMakeQTVRPanoramaの入力にして、パノラマムービーを作る、
それでは、その作業を実際にしてみようと思う。i_matさんから送って頂いた動画ファイル
を使い- 動画から静止画に変換し(走査線の狭間-1/60秒の世界を目指せ- (1999.07.08) 参照)、
- Image PC(NIH-imageをWindowsに移植したもの)で、走査線の一部を抽出し並べた静止画を作成する
もういきなり結果を出してしまおう。これが、「動画ファイルから走査線を抽出し、パノラマ写真にしたもの」である。
 |
おや?何が何だかわからない画像になってしまっている。変なモザイクがかかったみたいな画像になっているし、グレイ画像である。参考までに、先ほどの動画から手作業でパノラマ画像を作成したものを以下に示す。上の画像と比較してみると画像の示すものの対応がわかるだろう。
 |
さて、今回の実験結果が
- 変なモザイクがかかったみたいな画像になっている
- グレイ画像である
まず、
- 「グレイ画像」になっている理由
そして、「変なモザイクがかかったみたいな画像になっている」のは(動画中の)各画像から走査線をそれぞれ一本しか抽出しなかったからである。だから、横方向(カメラの撮影方向角度)のデータが足りないのである。そのため、モザイク画像のようになってしまったのである。
本来、抽出する走査線の数は、カメラの回転速度に応じて増やしてやらなければならないわけであるが、それが上手く合っていなかったのである。また、今回の画像を見て頂くと判ると思うが、動画ファイル自体も、実は一秒辺りのフレーム数が間引かれたものとなっている。それにより、抽出する走査線の数が一本ではますます足りなくなってしまっていたのである。
というわけで、今回は「失敗した」と言わざるをえない。何か、前回は「簡単である」などと言い切ったような気もするが、それはきっと気のせいであろう。
やはり、これは適当にあるもので間に合わせ仕事をしようとしたせいかもしれない。いつの日か「mov2panorama.exe」を作成し、必ずや必ずや再挑戦をするつもりである(Macでやるのは少しあきらめモード)。
2000-04-01[n年前へ]
■恋の力学 恋の相関分析編 
「明暗」の登場人物達の行方
「恋の力学」シリーズである。前書き編が登場したきりで、なかなか本編に入らない「恋の固体物理学」シリーズではない。今回は、
の続き、ということになる。以前、
の中で書いたように、恋の力学シリーズは夏目漱石の影響を多大に受けている。そして、同様に夏目漱石の影響を受けているシリーズがある。それは「文章構造可視化シリーズ」である。何しろ、「文章構造可視化シリーズ」は夏目漱石をきっかけとして、始まっているのである。また、シリーズの中の話を見ればわかるように、
- 夏目漱石は温泉がお好き?- 文章構造を可視化するソフトをつくる - (1999.07.14)
- 失楽園殺人事件の犯人を探せ- 文章構造可視化ソフトのバグを取れ - (1999.07.22)
- 「こころ」の中の「どうして?」 -漱石の中の謎とその終焉 - (1999.09.10)
- 「星の王子さま」の秘密- 水が意味するもの - (1999.11.15)
そのための準備として、まずは「文章構造可視化シリーズ」で作成した"wordfreq"をバージョンアップしてみた。その動作画面を以下に示す。
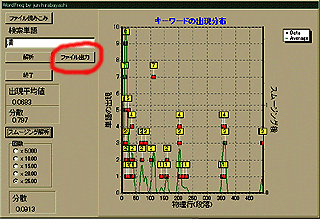 |
赤丸で示したボタンに「ファイル出力」と書いてあるのがわかると思う。つまり、文章中に「任意の単語」が出現した出現頻度を解析した結果をファイル出力する機能を持たせたのだ。1段落中に「任意の単語」が出現した数をテキスト形式で出力するようにしてある。このファイル出力結果を他のソフトに読み込めば、色々な解析ができるわけだ。いつものように、このソフトはここ
においておく。言うまでもないが、アルファ版の中のアルファ版だ。さて、今回用いるテキストは
でも登場した「明暗」である。そこで、「青空文庫」から「明暗」の電子テキストをダウンロードした。そして、バージョンアップした"wordfreq"で- 津田
- お延
- 清子
- 吉川
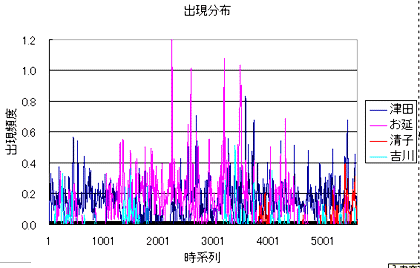 |
しかし、これだけでは、よくわからない。せいぜい「清子」が小説の後半(といっても、未完であるが)に登場しているなぁ、という位だろう。しかし、さらに解析を加えてみると、もう少し面白いことがわかる。
今回は、これらの登場人物間のお互いの関わりを調べたいのである。であるならば、これらの「登場人物」の出現分布の間の相関を調べてみると面白いだろう。互いの関係を示す「相関」を調べてみるのである。異なる「登場人物」が同じような出現をしているならば、それは無関係ではない。きっと、その登場人物の間には何らかの関係があるに違いないのだ。
そこで、「明暗」を時系列的に6つの部分に分けて、津田と他の登場人物の出現分布間の相関を調べてみたのが次のグラフである。
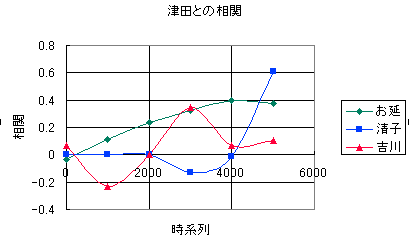 |
このグラフでは、横軸が時系列であり、縦軸が相関を示している。縦軸で上になればなるほど相関が高い、すなわち、「関係がある」のだ。「相関」は本人の場合で「1」である。だから、例えば最後の部分の清子の「0.6」という結果は関係がアリアリということを示しているわけだ。
また、「清子」と「吉川(ここでは夫人を意図している)」の相関が逆であることが面白いだろう。「吉川」が活躍(暗躍?)した後に、「清子」が登場するわけだ。
そして、この「明暗」が盛り上がっていくようすすら、見えてはこないだろうか?全く血の通っていないPCが解析した結果が、漱石の描こうとした「こころ」の動きを読みとっているような気が(少しは)しはしないだろうか?そして、このグラフの延長線上に、漱石の描くはずだった、「明暗」の結末はあるはずなのだ。
さて、このグラフを見ていると、
で計算した恋の多体(三体)問題の計算結果を思い出してしまう。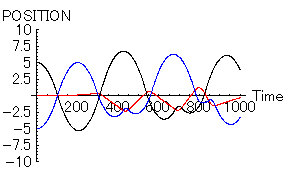 |
漱石は、きっと恋の三体問題を意識しながら「明暗」を書いたのである。だから、ある意味当然なのではあるが、科学と文学の一体化した世界が感じられ、とても面白い気分である。さて、この解析結果を元にして、まだまだ色々とやってみたのであるが、それは次回である。
2000-08-26[n年前へ]
■恋の力学 
そう言えば以前referer_logを解析したときに、「恋の力学 -恋の無限摂動 - (1999.12.21)」をほとんどそのまま流用して大学に提出するレポートに仕立てたものを見かけたなぁ。

