2000-09-02[n年前へ]
■もうすぐ二歳の「できるかな?」 
初心に帰ってみましょうか?
「できるかな?」が始まったのは二年近く前の秋のことだった。
でも触れたが、当初(実は今も続いているが)は某社内の某サーバー内でこっそりと始めてみたのだった。それから二年あまりでずいぶんと色々な話が増えた。某社サーバー内でしかアップしていない- プリンタドライバーは仮免
- 続 電子写真プロセスを分数階微分で解いてみよう
- 続々 電子写真プロセスを分数階微分で解いてみよう
そして話が増えてきたせいか、自分自身でも「アレッ、あの話はどこにあったけ?」というように迷ってしまうことが多々ある。迷うどころか、最後まで見つからないこともしばしばあるのだ。そして、それは私でもない他の人であればましてやそうだろう。というわけで、
では簡単にそれまでの話の紹介をしたし、ではhirax.net内の全文検索機能を付けてみた。今回は、これまでの話題をもう一度自分で読み直して、その中から「自分のお気に入り」を調べてみたいと思う。そして、最近少し話題が変になってしまっている反省をして、もう一度初心に帰ってみようと思うのだ。
まずは、1998年の話題からいくと
というあたりが、良い感じだ。京都の風物詩である「鴨川カップル」達が人目を気にしながら寄り添う合う姿を考えてみたものだ。後の「恋の力学」シリーズなどはここらへんから始まっていた、といっても良いだろう。そしてこの頃の[Scraps]系の話題としては、がある。少し前に、この「さなえちゃん」を描いた漫画の作者からメールを頂いたのがとても私には印象深かった。そして、1999年の上半期から選んでみると、まずは
というところだろう。ハードディスクの情報を可視化することで情報圧縮・エントロピーを考えてみた一話である。そして、同じような「可視化シリーズ」の一つである- 感温液晶でNotePCの発熱分布を可視化する- 熱いところで感じてみたい St.Valentine 記念 - (1999.02.14)
- NotePCの発熱分布を比べてみたい- お熱いのがお好き SOME LIKE IT HOT - (1999.02.15)
そして、1999年の下半期はもう自分で言うのも何だが傑作揃いである。大体、書いているペースが自分でも驚くくらいのハイペースだ。月当たりの話の数を数えてみると、
- 7月 9話
- 8月 9話
- 9月 8話
- 10月 8話
- 11月 11話
- 12月 9話
この頃の「お薦めの話」はいっぱいある。例えば、
に始まった「文章可視化シリーズ」や、で始まった「ASCIIアートシリーズ」だろう。から始まる「江戸五色不動シリーズ」は江戸にロケまで行ったので、とても思い出深い話の一つである。しかも、妙な偶然のせいでまるで小説の中に迷い込んだような気持ちになったものだ。そして、WEBページを作る上では
などもどうしても外せない。そして、この後結構続くことになるという「恋の力学」シリーズもこの時期に始まっている。そして、この頃の一番人気が何と言ってもだろう。この「ミニスカート」系の話の流れは以降も続くことになるのが自分では意外でもあり、残念でもある。それはさておき、ナンセンス系ではなんてのも面白い話だと思う。そして、1999年の終わりはやはりこれが「お気に入り」の話である。また、[Scraps]系の話がこの時期にはやたらいっぱいあるのが面白いところだ。その内からいくつかピックアップするとこんな感じだろうか?- [Scraps]絵馬 - どこにもいないよ- (1999.07.09)
- 新宿駅は電気羊の夢を見るか- 意識とは何か - (1999.07.10)
- [Scraps]合掌 - キレイはキタナイ、キタナイはキレイ- (1999.08.01)
- [Scraps]いつかきっと -掌の中の答え - (99.11.03)
- 「文学論」と光学系 - 漱石の面白さ-(2000.02.27)
- 恋の力学 恋の相関分析編- 「明暗」の登場人物達の行方 - (2000.04.01)
- 恋の力学 恋のグラフ配置編- 「明暗」の収束を見てみよう - (2000.04.02)
- 恋する心を見てみたい - 恋のきっかけはどの出来事?- (2000.05.14)
- 恋の形を見た人は - 恋の相対性理論- (2000.05.17)
さて、今回は2000年上半期までの話の中から「私の好きな話」を振り返ってみた。とはいえ、私の好きな話=他の人の好きな話ではないようだし、他の話も適当に眺めて頂いたら良いかなぁ(私が)、と思うのだった。
2000-09-16[n年前へ]
■モザイク消し器の真実 
買うも買わないもアナタの自由
で「モザイク消し器」について考えてみた。といっても、考えてみただけで使ってみたわけではない。当たり前である。そんな「モザイク消し器」が私の家にあるわけはないからだ。歩く「悟り」、歩く「生き仏」と呼ばれる私の家にそんなものがあって良いはずがない。その証拠に私はそんな風に呼ばれたことがない(土屋賢治風ロジック)。モザイクの向こう - 隠しているから良いのです- (2000.07.18)
さて、そんな風に言いたい所なのだが、実はそれがあるのだ。何と、「モザイク消し器」が私の家には鎮座しているのである。といって、それは私のものではなくて、某編集者の方がとあることのために送ってくれたものなのである。
 |
残念ながら、このくりくり小僧はあまりにも使い物にならなかったので、部屋の片隅にそのまま放置されていた。いや、こう書くと誤解されそうである。別に変なことに使ったわけではなくて、技術的に使い物にならなかったのである。一応、そこの所はハッキリしておきたい。大体、コレを一体どうやって変なことに使うのだ(以下略)。
今回、このくりくり小僧を送り返すことになったので、せっかくだからこのモザイク消し器がどんな風に技術的に使い物にならなかったかをこのタイミングで書いてみることにしたいと思う。
まずは、このくりくり小僧の操作方法を説明しておこう。ビデオ信号は通常のNTSC信号で入出力するようになっている。エロビデオをこの「くりくり小僧」に入力し、処理した画像をテレビへ送るのである。あるいは、処理した画像を新たにビデオにダビングするのかもしれない。
この「くりくり小僧」は、対応するモザイク処理(広義の)の種類は
- モザイク(狭義の)
- 反転
 |  |  |
「くりくり小僧」の写真を見ると判ると思うが、画像復元処理をかける領域の
- 大きさ
- 位置
写真中にあるその他のボリューム
- 輝度
- 明るさ
- エンハンサー
それでは、まずは適当にモザイク画像を作ってみる。そして、その画像を「くりくり小僧」を使ってキレイに戻せるかを調べてみることにしよう。そこで、最初に示すのが
- 女性のオリジナル画像
- オリジナル画像の一部に反転処理をかけたもの(後述するが、実は失敗している)
 |  |
上の右の反転画像の中央部に対して、「くりくり小僧」で復元処理をかけてみたのが下の画像である。さて、画像は元通りになっているだろうか?
 |
この画像を見る階調は確かに反転しているのであるが、色が明らかにおかしい。オリジナル画像では赤かったハズの唇が青いのである。それどころか、顔全体が青いのである。真っ青だ。明るさは正しそうなのであるが、色合いは絶対に何かが狂っている。
そこで、「基準画像」に対して、「くりくり小僧」で反転復元処理をかけてみることで、どのような処理をかけているかを調べてみた。それが下の画像である。左が「基準画像」で、右が「基準画像」に「くりくり小僧」で反転復元処理をかけてみた画像である。なお、画像の右端および下端部分に関しては「くりくり小僧」で反転復元処理をかけていない。
 |  |
さて、画像の向かって左にあるグレイスケールの階調部分を見れば一目瞭然だと思うが、この「くりくり小僧」で反転復元処理をかけた画像は確かに明るさが反転している。それはその他の白黒画像の部分を見ても明らかである。
そして、カラーチャート部分を見てみると、色合いは実は全く変化していないことが判る。右上から左下まで「紫・青...橙・赤」と繋がっているカラーチャートは左と右でそれほど違っていない。ほとんど同じである。
それは考えてみれば、当たり前なのである。「くりくり小僧」の入出力はNTSC(NationalTelevision System Commitee)方式を使っている。このNTSC信号はカラー画像を
- 輝度情報
- 赤 - 輝度情報
- 青 - 輝度情報
- 赤 - 輝度情報
- 青 - 輝度情報
ところが、先ほど私が女性のオリジナル画像に対して反転処理をかけてみたものは、RGB画像のRGBそれぞれのチャンネルに対して反転処理をかけていたのである。これでは、明るさが反転するだけでなくて、色合いまで反転してしまう。私は、何と「くりくり小僧」の入出力はNTSC方式を使っていて、RGB画像でないことを失念していたのである。その結果、女性の顔色が反転したまま真っ青になってしまったわけだ。
そこで、その「輝度チャンネルのみの反転」ということを考慮してテストしてみたものが次の画像である。今度は反転画像の中央部に「くりくり小僧」で復元処理をかけた部分の色合いが正しい色合いであることがわかるだろう。
 |
なるほど、「反転画像」に関しては「くりくり小僧」は確かにちゃんと画像を復元できることが判った。しかし、しかしである。反転モザイク処理をかけたビデオなんてそうそうあるわけがない。いや、そんなに自信を持っていうと何やら変な疑いをかけられそうであるが、多分そうだろう。ほとんどは、次に示すモザイク(狭義の)処理だと思う。それをキレイに復元できなければ、「モザイク消し器」と名乗る資格はない。そうは思わないだろうか?百歩譲っても、「反転消し器」と言うべきではないだろうか?そこで、狭義のモザイク画像に対してこの「くりくり小僧」が威力を発揮することができるかどうかを、次に調べてみた。
まずは、作ったモザイク画像を先に示そう。下の左が先程と同じオリジナル画像で、右がモザイク(狭義の)画像である。よく(?)見かける画像だと思う。
 |  |
それでは、「くりくり画像」はこのモザイク向こうをキレイに映し出すことができるだろうか?この機械は悩めるエロ子羊達を救うことができるのだろうか?それを確かめてみたのが次の画像である。先のモザイク画像の中央部に「くりくり小僧」で復元処理をかけてみたものである。
 |
「何だこりゃぁあぁ」、と私は思わず叫びそうになった。いや、別にこの機械のためにお金を払ったわけじゃないから良いのだけれど、一体なんなのだこれは。このモザイク消し機能はハッキリ言って大嘘である。桃太郎侍だったら「おまえなんか「モザイク消し器」じゃねぇぇ」と切り捨てるところだ。
これなら、前回
で試したような単なるボカシ処理の方がずっと上である。ちなみに、この下の画像が単なるボカシ処理で「モザイク」を消してみたものである。上の「くりくり小僧」の復元画像よりもずっとマシであることが判るだろう。モザイクの向こう - 隠しているから良いのです- (2000.07.18)
 |
ちなみに、先程の「反転処理」の場合と同じように、「基準チャート」に対して「くりくり小僧」でモザイク復元処理をかけてみたものを示してみよう。下に示すその画像を見れば、「くりくり小僧」のモザイク復元処理が
- 輝度チャンネルの反転処理
- 横方向のエッジ強調処理
 |  |
しかし、この「モザイク復元処理」をかけてみても、私には全然モザイクの向こうは見えないのである。もう、何が何だか判らないのである。もう、何が何だか判らないが故に、もしかしたら人の持つ無限の想像力をフルに発揮できるのではないか、と思うほどである。私は残念ながらエロの想像力が足りないのかもしれないが、想像力の発達したエロの天上人達であれば話は別だろう。
さて、今回の話は「モザイク消し器のMTF(仮称)」というタイトルで書き始めたのであるが、「モザイク消し器」の実力がこんなものだったのでお蔵入りしていたのである。まぁ、解析の出来としてはイマイチであるが、もしかしたら「モザイク消し器」を買おうかどうかと迷っている子羊達の参考になるかもしれないので、一応公開してみた次第だ。
さて、私はこの機械をいじってみて思わず暴れ出しそうになったが、それはもしかしたら私だけかもしれない。人によっては、「何て素晴らしいんだ!!この機械は!!」と感激する可能性だってゼロではない。イマジネーションが豊かなあなたであれば、さぞかし素晴らしい桃源郷がモザイクの向こうに見えるのかもしれない。
だから、「買うか、買わないか」はアナタの自由だ。だから、このイマジネーション養成ギブスに大枚を払うの悪くないかもしれない。この機械でイマジネーションを鍛えた暁には、モザイクの向こうにアナタには何かが見えるかもしれない。確かに、それも悪くないかもしれないだろう。そこに何が見えるかは、結局あなた次第だと思うのである。
2000-11-07[n年前へ]
■SEXYタレント売り出し術 
または恋のフライバイ
朝のテレビと言えばテレビ朝日の「やじうまワイド」である。私はニヒルな吉澤アナウンサーが大好きなので、毎朝TVのチャンネルを「やじうまワイド」に合わせておくのが日課なのである。
吉澤アナの素晴らしさを少し語らせてもらえば、コメンテーターが変なコメントを言った場合、吉澤アナは即座に「本当にそうですかねぇ?」といとも簡単に否定する。しかも、深夜番組ではなく、早朝のさわやかな時間帯にである。コメンテーターの威厳などあったものでない。しかし、コメンテーターの威厳というモノがそんな言葉で否定されるようなならば、そんなものは実は「張りぼて」のような威厳であるわけで、その張りぼてを日の下にさらしてしまうそのイケズな感じが私は実に大好きなのだ(そしてそんな斜に構えた吉澤アナがホントーにたまに真剣な目になる感じが私は同時に大好きだ)。
とりあえず、そんな感じで毎朝「やじうまワイド」を流していると、梨本勝とか福岡翼などの芸能レポーター達が芸能スキャンダルをしゃべりまくり、いやでもそれらが耳に入ってくるのである。朝のTVはと言えば、何はなくともまずは芸能スキャンダルなのだ。といっても、私の耳は興味のないことにはかなりの難聴気味になるらしく、それらの芸能スキャンダルは耳には入ってくるのだが残念ながら頭には入ってこない。
そんな私でも、芸能オンチの私でもスキャンダルを利用した「SEXYタレントの売名行為」が多いことには驚いてしまう。古くは(そんなに古くない?)「古屋一行のAVギャルスキャンダル」から、「羽賀研二と桜庭あつこ」や「岡村隆史と美人巨乳釘師」まで、そんな話は腐るほどある。
確かにそんな話は腐るほどあるのだが、SEXYタレント売り出し術を科学的に考察したという話は今だ聞いたことがない。私が不勉強なせいかもしれないが、少なくとも私は聞いたことがない。
一体、それはナゼだろうか?ミョーに科学的な芸能プロダクションあたりが、そんな研究をしないものなのだろうか?もうすぐ21世紀になるというのに、そんな科学的な芸能プロダクションは存在しないものなのだろうか?
いやもちろん、そんな芸能プロダクションはないだろうし、そんなクダラナイことも誰もあえてするわけもないだろう。しかし、クダラナくて誰もそんなことをしないというのであれば、それはもう本サイトの大好きなジャンルである。というわけで、今回は「SEXYタレントの売り出し術」を考察してみることにした。
まず、芸能に疎い私が考えてみるに、なぜかだか知らないが「SEXYタレントの売り出し術」は「愛」を装うのが普通である。「古屋一行のAVギャル」でも、「羽賀研二と桜庭あつこ」でも、「岡村隆史と美人巨乳釘師」でもいずれも「始まりはいつも愛」なのである。こう書くと「ちょっといい話」に聞こえるが、実は全然「いい話」ではないのが不思議と言えば不思議であるが、とりあえず「SEXYタレントの売り出し術」は「愛」の一応用例として考えることができるかもしれないわけだ。
本WEBサイト「できるかな?」でも「愛」ならぬ「恋」の力学は常日頃から考えているわけで、「恋の力学」が解けるなら、「愛の力学」も解けるかもしれないし、だとしたら、「SEXYタレントの売り出し術」も解けると言っても必ずしもウソとは言えないだろう(典型的な詭弁)。そこで、今回はこれまで考えてきた「恋の力学」を応用することで、「SEXYタレントの売り出し術」を考えてみることにした。
とりあえず、登場人物として次のような三人を考えてみよう。
- 登場人物 男性タレントA : 名実共にA級のタレント。
- 登場人物 男性タレントB : B級タレント。沖縄に店を経営していたりする。女性に「誠意」を見せるのが得意中の得意。
- 登場人物 女性タレントC : C級タレント。少なくとも私には「誰だそれ」状態の無名人。だけど、大抵の場合SEXY度だけはバツグン。
つまり、
- 女性タレントCがはるか遠くから男性タレントAに近づいていく
- 女性タレントCと男性タレントAが最接近する
- 女性タレントCが男性タレントAから離れ、ずっと離れた方に行ってしまう
- 女性タレントC
- 男性タレントA
しかも、男性タレントAの存在感と女性タレントCの存在感はあまりに差がある。そのため、女性タレントCが近づいてきても男性タレントAはビクともしない。もちろん、もともと男性タレントA自身は芸能界の中をどっしりと動いているわけであるが、女性タレントCが近づいてきても我関せずである。それに対して、女性タレントCは男性タレントAに近づくことで影響を受ける。
このような場合は単純なケプラー運動の一例であり、細かい導出はメンドくさい(私が)のでしないが、女性タレントCは男性タレントAの近くでは、彼を基準とした座標系で双曲線軌道を描く。普通であれば「双曲線軌道」という言葉には何の色っぽさもないが、コトが「SEXYタレントの売り出し術」であるだけに、双曲線軌道という言葉でさえ何か色っぽさを感じてしまうのは私だけだろうか?
そんなことはおいておいて、女性タレントCは男性タレントAに近づいて、そして離れていくのである。その時、彼女は彼を基準とした座標系で双曲線軌道を描くわけだ。
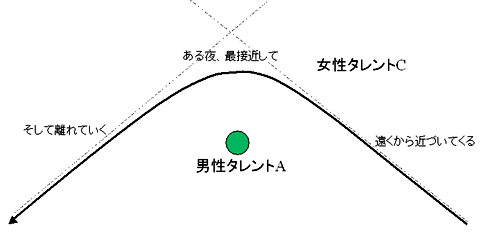 |
この場合、女性タレントCの「イキオイ」(ここでは速度とでもしておこう)は男性タレントAを基準とした座標系では「一番最初に近づいてくる時」と「一最後に離れて行く時」では変わらない。もちろん、方向は違うのだが、大きさは同じである。それを描いてみたのが次の図である。女性タレントCのイキオイは最初と最後では、方向が違うだけで大きさは同じコトがわかるだろう。
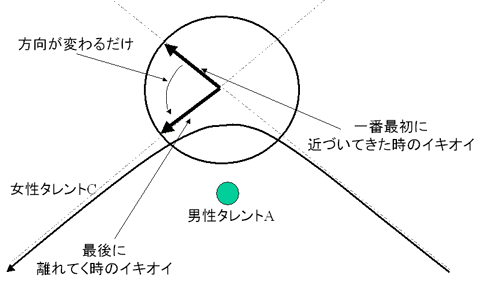 |
この場合、「SEXYタレントの売り出し術」としては単に女性タレントCの方向転換を図っただけ、である。図に書くとこんな感じだ。
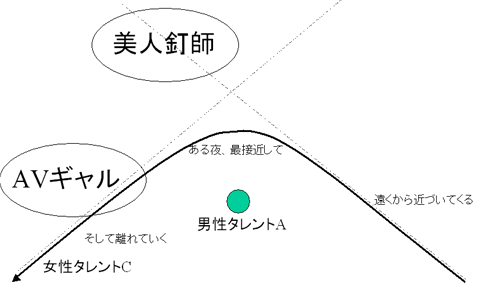 |
ちょっと具体的すぎたような気もするが、この例はフィクションにすぎない。別に男性タレントAがナイナイ岡村だと言っているわけではない、と一言だけフォロ〜しておくことにしよう。
さて、この場合の「SEXYタレントの売り出し術」はかなり低レベルなテクニックである。これは単に女性タレントCの方向転換ができただけである。それ以外のさしたる効果は何もない。
しかし、これまで考えてきた「恋の力学」を応用して考えるに、さらなる高度な「SEXYタレントの売り出し術」が考えられる。それはどのようなテクニックかと言えば、相手すなわち男性タレントAのイキオイを利用するのである。日本のお家芸の柔道のように、相手の力を利用してそれを自分のモノとするのである。
こちらは、結構ハイテクニックなので判りにくいが、それをなんとか絵にしてみたのが次の図である。この場合、「男性タレント自身にもともとイキオイがある」ことが重要である。すなわち一般視聴者を基準とした座標系に対して、男性タレントA基準系は動いているのである。
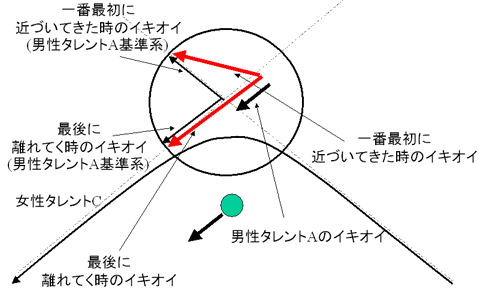 |
すると、一般視聴者を基準とした座標系では、面白いことに女性タレントのイキオイ自体も男性タレントに接近する前と後で変わるのである。もちろん、上の図を見てもらうと判るように、男性タレントA基準系では女性タレントのイキオイは方向が違うだけで、大きさはなんら変わっていない。しかし、それは男性タレントA自身がイキオイがあるためで、一般視聴者を基準とした座標系では女性タレントCのイキオイは増しているのである。赤い線で描いた「一般視聴者を基準とした座標系での女性タレントCのイキオイ」が最初と最後で違っているのが判るだろう。つまり、女性タレントCはこの接近戦でイキオイが増しているわけだ。これが比較的高度な「SEXYタレントの売り出し術」である。このテクニックを使えば、男性タレントの背後から近づけば女性タレントCのイキオイは必ず増すということになる。
さて、それでは女性タレントCの接近相手が
- 男性タレントB : B級タレント。沖縄に店を経営していたりする。女性に「誠意」を見せるのが得意中の得意。
そして男性タレントB相手の場合には、もうひとつ問題がある。相手が名実共にA級のタレントAであると、タレントAは女性タレントCが近づいたくらいではビクともしない。しかし、それがタレントBの場合だと、あまりに重みがないために女性タレントCがタレントBに近づくと揺れ動いてしまうのである。そんな状態では「SEXYタレントの方向転換」すら上手く行くかどうか判ったものではない。誠意大将軍の彼を頭に浮かべて頂ければ、おそらく納得して頂けると思う。
さて、今回は相手の力を利用して自分のイキオイを増す「SEXYタレントの売り出し術」方法を考えてみた。もちろん知っている人も多いだろうが、これはフライバイ(flyby)とかスイングバイ(swingby)と呼ばれるテクニックで、ロケットの軌道制御などに使われるテクニックだ。それを「SEXYタレントの売り出し術」に応用してみたわけだ。
最初の方に書いたとおり、今回は「SEXYタレントの売り出し術」は「愛」の一応用例として考えてみたのだから、このフライバイを「恋・愛」に適用してみるのも面白いのではないだろうか?例えば、あなたが誰かに恋をして、その恋をすることで自分自身も輝いたりイキオイが生まれることがあるはずだ。このフライバイを行う限りは、相手とはすれ違うだけで、いずれ遠くへ離れてかざるをえないわけであるが、少なくともその「恋・愛」であなたが成長することもあるだろう。相手の後ろから追いかけて、そして少し方向を変えてまた離れていくときに、イキオイは必ず増すだろう。それは一つのフライバイ、「恋・愛」のフライバイと言っても良いのではないだろうか、と思ったりするのである。もちろん「SEXYタレントの売り出し術」と同じで、それは結局相手次第だと思うけどね。
2000-11-26[n年前へ]
■ブランコの中の∞(無限大) 
なんで一体漕げるのだろう?
公園のブランコというのは、何故かとても不思議な雰囲気を持っている。ホントにうるさいくてたまらないくらいのガキんちょ達が、アクロバットのようなスゴイ技を見せていたりする。それは、まるで上海雑伎団を見ているような気分になる。小さな子がなかなかブランコが漕げず、ブランコの上で宇宙遊泳のように四苦八苦しているのを見ているのも思わず笑ってしまうくらいに可愛らしいものだ。もちろん、そこは子供の領分というだけではなくて、黒沢明の「生きる」の主人公がしていたように「大人がブランコに座って揺れていたり」すると、思わずその人の陰に隠れている物語を想像したりしてしまう。ブランコの周りというのはそんな不思議な雰囲気を持っているのだ。
やたらにブランコを漕ぐのが上手いガキんちょもいる一方で、全然ブランコを漕げず四苦八苦する子供もいる。ブランコを漕ぐコツを覚えるのもなかなか大変そうである。考えてみれば、ブランコは一体どういう風に漕ぐものなのだろう?口で上手く説明できる人がいるだろうか?
それに、そもそも私たちはブランコを何故漕ぐことができているのだろう?
いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか?という手紙で始まるのは加納朋子の「ななつのこ」だが、「何故、リンゴは落ちるのかという謎」と同じく、「ブランコの漕ぎ方の謎」だってとても不思議だ。いつも目にする公園のブランコを、私たちは一体どうやって漕ぐことができているのだろう?
いつだって、どこでだって、謎はすぐ近くにあったのです。
何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。
もちろん、「何でブランコの漕ぎ方が不思議なのさ?」と言う人も多いだろう。その中には理路整然とブランコの漕ぎ方を説明してくれる人もいるだろう。そして、「特にブランコの漕ぎ方をじっくり考えたことなんかないもんね」という人も多いに違いない(私だけかもしれないが)。そこで、まずは「ブランコの不思議」を簡単に書いてみることにしよう。
次の図は「ブランコを漕いでる子供」である。
 |
この子供が何もせず立っているだけ(あるいは座っているだけ)だったら、どうなるだろうか?それはもちろん、単なる振り子と同じくようにブランコは動く。もしも色々な摩擦がなければ、まったく同じように動き続けるだけだし、摩擦力があればブランコの動きはただ減衰していくだけである。つまり、子供が何もしなければ、ブランコの動きは「遅く・小さく」なることはあっても、ブランコが「速く・大きく」なることはないのである。
だからブランコを速くするためには、「ブランコに乗ってる子供がブランコを漕がなければならない」わけであるが、ブランコに乗ってる子供は一体どんなことができるだろうか?
次に示す図は「ブランコに乗ってる子供を中心にとった座標軸」を描いてみたものだ。この図の中で直交する二つの軸を描いてある。つまり、
- ブランコの動きの中心を向いている軸A
- 軸Aに直交する、つまりブランコの進行方向(あるいはその逆方向)を向いている軸B
 |
ところが、実は「ブランコに乗ってる子供」はこの二つの軸の内の片方、軸Aに対しての動きしかできない。何故なら、軸B方向に対しては「ブランコに乗ってる子供」動きの支えになるモノが全然無い。だから、ツルツル滑る氷の上では全然動けないのと同じく、「ブランコに乗ってる子供」はその方向には動けないのである。もし子供がその方向に動こうとして体を動かしたりしても、結局子供の重心はその方向には全然動かないのだ。
それに対して、ブランコの動きの中心を向いている軸A方向に対してはブランコの鎖も座っている(あるいは立っている)板が支えになるわけで、その方向に対しては「ブランコに乗ってる子供」は動くことができる。
というわけで、ブランコの上では「ブランコの動きの中心を向いている軸A」方向にしか動けないわけであるが、その方向というのはブランコの進行方向に対しては直交している。つまり、ブランコを漕ぐためには、「ブランコの進行方向に対して直交している方向に動く」しかないことになる。
ここまで書くと、ブランコの不思議が判るハズだ。ブランコを漕ぐ、つまりブランコを軸B方向の速度を上げたいのに、我々は「軸Bに対して直交している方向に動く」ことしかできないのである。一体何故、軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増すのだろうか? この謎「ブランコの不思議」を、ゆっくり考えてみることにしよう。
まずは、ブランコに乗ってる子供が立ち上がったりして、「ブランコの動きの中心を向いている軸A」方向に動いた場合、何が起きるだろうか?
 |
「ブランコの動きの中心を向いている軸A」方向に動くと、ブランコの鎖の長さが短くなることと同じである。すると、回転しているブランコの鎖が短くなるわけで、そうするとブランコの速度は速くなる。何故なら、角運動量が保存されるからである。ちょうど、スケートのフィギア競技の選手が回転中に伸ばしていた手を縮めると回転数が早くなるのと同じだ。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの半分だけ(とんでもない身長の子供だ!)上がれば、ブランコの速度はもとの速度の倍になるのである!
ということは、少なくともこの瞬間は「軸A方向に動いたハズなのに、それに直交する軸B方向の速度が増す」わけであるが、これでブランコの漕ぎ方を納得するにはまだまだ早いのである。確かに、「ブランコの動きの中心を向いている軸A方向に動く」とブランコの速度は増すわけであるが、それはその瞬間だけである。ブランコの上で「立ち上がり続ける」なんてことはできないわけで、速度が増し続けるわけではないのである。
もしも、「もう一度ブランコの上で立ち上がるために、すぐに低い姿勢に一旦戻ったり」したら大変だ。ブランコの鎖の長さが長くなるのだから、今度はブランコの速度は遅くなってしまうのである。
もし、ブランコに乗ってる子供の重心がブランコの鎖の長さの二倍だけ(つまりさっき立ち上がった逆の動きである)下がれば、ブランコの速度はもとの速度の1/2になってしまうのだ!
これでは、結局さっきの速度が二倍になったことは帳消しになってしまう。つまり、「単純に」角運動量の保存を考えるだけではブランコの速度を(長い間にわたって)早くしていくことはできないわけだ。
このままでは、「ブランコを漕ぐことなんか不可能である」という結論が出てしまいそうになるが、ブランコを漕いでる子供達はイッパイいるわけで、そんな結論を受け入れるわけにはいかない。彼らがみんな超能力でブランコを漕いでいるわけもないのである。まだまだ見落としていることがあるので、ブランコの不思議の謎が解けないだけのハズなのだ。
そこで、ちょっと考えてみると「とんでもなく単純なこと」を見落としていたことに気付いた。それは、「タイミング」である。例えば、ブランコの速度がずっと同じであるすると、
- 初期のブランコの速度 = 10
- 重心位置を高くして 10 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- 重心位置を低くして 10 X 1/2 = 10 (何てこったい、速度が半分になっちまったか!)
- 初期のブランコの速度 = 10
- 重心位置を高くして 0 X 2 = 20 (やったぁ、速度が二倍だぁ!)
- そのあとブランコの速度 = 0
- 重心位置を低くして 0 X 1/2 = 0 (0が0になっても全然変わってないもんね!ヘヘン!)
人生何事もタイミングが重要である。失恋した男性や女性にタイミングをわきまえた「恋のハイエナ」達が寄ってくるのと同じく、またお金に困っていると何故かサラ金の広告が目の前にチラチラするのと同じく、ブランコを漕ぐにはやはりタイミングが重要なのだ。
なるほど、考えがまとまってきた。このイキオイでそのまま「ブランコの理想の漕ぎ方」まで考えてしまおう。
まず、「重心位置を高くしてブランコの速度早くする」にはできるだけ速度が速い瞬間に行うのが良いだろう。倍率が確定している賭なのだから、元金はあればあるほどおトクである。1万円×2=二万円では1万円しかもうからないが、一千万円×2=二千万円では一千万ももうかるのだ。ブランコの速度が速い瞬間に立ち上がれば、一番おトクに速度を増すことができるのである。
もちろん、ブランコの速度が速い瞬間といえば、明らかにブランコが一番下にきた瞬間である。つまり、ブランコが一番下にきた瞬間に立ち上がれば「一番おトクに速度を増すことができる」わけだ。しかも、その瞬間は鉛直に重心を持ち上げることになる。つまり、位置エネルギーを効果的に増加させることができるわけだ。結局、この時に増加させた位置エネルギーは後で、運動エネルギーに変換されるわけで、結局これがブランコの運動の源となるのである。
そして、「次にもう一度立ち上がるために一旦低い姿勢に戻る瞬間」=「速度が遅くなる瞬間」はブランコが停止しているときであれば何の問題もない。ブランコはもともと止まっているんだから、その速度が何分の一になったって全然気にしないもんね!となるわけだ。そのタイミング= ブランコが止まる瞬間といえば、もちろんブランコが最高地点まで上がった瞬間である。つまり、ブランコが一番上にいった瞬間に低い姿勢に戻れば全く減速無しに次の加速に備えることができるわけである。しかも、その時には実は運動エネルギーを位置エネルギーに変えることで、隠し財産にしているわけで、もう汚い政治家のマネーロンダリングのような見事な方法なわけだ。
というわけで、
- ブランコが下に来たときに(立ってる場合は)足を伸ばして立ち上がったり、(座ってる場合は)足を曲げたりすることにより高い位置に重心を持ってきて(しかも、重力に逆らって重心を上げるため位置エネルギーが増加する)
- ブランコが上に行ったときにその姿勢を元に戻す
それでは、確認のためにそのやり方で本当にブランコが漕げるのかどうか、シミュレーション計算を行ってみた。ブランコの動きは振り子運動だが、振れ幅がとても大きいので、cosx≒xというような近似をする単振動としての扱いはできない。そこで、楕円積分の計算を行わなければならない。が、私が自分の力でできるかどうかはともかく、そこはMathematicaに解かせればイッパツである。もう、驚くくらい簡単なのである。自分の力で解いていないところが、実に悲しい現実ではあるが、それが現実なのだからしょうがない。
というわけで、ブランコの動きのシミュレーションをしてみた結果が次のグラフである。「ブランコに乗ってる子供」の漕ぎ方としては、以下の三つ
- 何もしない場合
- ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合
- ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合
 → ブランコの動きはず〜と変わらない |
ブランコが上にきたあたりで座り込んだ場合  → ブランコの動きはどんどん大きくなる 「やったぜ、これが理想の漕ぎ方だぁ。」 |
ブランコが上にきたあたりで立ち上がった場合  → ブランコの動きはどんどん小さくなる 「なんてこったい、遅くなっちまったぁ。」 |
この結果から、ちゃんと1.の「何もしない場合」は「ブランコの動きはず〜と変わらない」し、理想の漕ぎ方であるハズの2.の「ブランコが下にきたあたりで立ち上がり、ブランコが上にきたあたりで座り込んだ場合」は「ブランコの動きはどんどん大きくなる」し、最悪の漕ぎ方であるハズの3.の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合」には「ブランコの動きは逆にどんどん小さくなってしまう」ことがわかる。というわけで、今回考えた「ブランコの不思議= 漕ぎ方」はシミュレーション計算結果からも確かめることができたわけだ。
ところで、こういったタイミングを考えながらパラメーターを変えることで動きを大きくしたりすることは「パラメータ励振」と呼ばれる。ブランコの漕ぎ方はその「パラメータ励振」の応用のひとつである。「何故、リンゴは落ちるのかという謎」には重力という基本的な物理現象が隠されていたが、それと同じく、「ブランコの漕ぎ方の謎」にも「パラメータ励振」という物理現象が隠されているのだ。次回以降も、この「パラメータ励振」を手がかりにいくつかの「身近な謎」に迫ってみたい、と思うのである。
さて、公園でブランコを漕ぎまくる子供をもし見かけたならば、ぜひ横から子供の動きを見てやってもらいたい。きっと、その揺れ動くブランコの中にはこんな∞(無限大)の形が見えるハズだ。天まで上ろうとする「ブランコの秘密」はその「ブランコの中の∞(無限大)」に隠されていたのである。子供も含めて人間の可能性は∞(無限大)だと私は思うが、ブランコの揺れる動きから、そんなことを考えてみるのも少し面白いのではないだろうか? それとも、ちょっと考え過ぎかな。
2000-12-01[n年前へ]
■続々オッパイ星人の力学 
胸を揺さぶるパラメータ励振 編
前回、
では、純真でピュア〜な幼心に戻って公園で大きく揺れるブランコの動きを考えてみた。近所の公園でよく見かける、小学生位の子供達が一心不乱にブランコを揺らす景色の中に隠れている科学をちょっとばかり考えてみたわけだ。そして、「ブランコの漕ぎ方の謎」の中には「パラメータ励振」という物理現象が隠されていることを眺めてみた。動きの周期のタイミングに合わせて、パラメーターを変えてやることでブランコの振動を大きくしていたのだった。ところで、公園でブランコを揺らす子供達と同じく、純真でピュア〜なのが生まれたばかりの乳児達である。もちろん、そんな乳児達はまだまだ公園でブランコを揺らすなんてことはできなくて、大きく成長するために母親の母乳を飲んで、そしてただひたすら眠る毎日を過ごしているのである。
そんな乳児の頃の純真でピュア〜な気持ちを、大人になっても持ち続けている人達もいる。そんな純真でピュア〜な大人達は大人になっているにも関わらず、生まれたばかりの乳児と同じくオッパイに惹かれ続けているのである。そして人は彼らをほんの少しばかりの尊敬と沢山の侮蔑を込めて「オッパイ星人」と呼ぶのである。
これまで「できるかな?」では、そんなオッパイ星人達の科学である
を考察してきた(いやもちろん目的はオッパイ星人と闘うためであって、女性を守るためであることはもう一度ここで確認しておきたい)。今回は「純真でピュア〜」をキーワードにして「子供達がブランコを揺らす景色の中に隠れている科学」と同じように、「オッパイ星人の力学」について考えてみたい、と思うのである。
まずは、次に示す「純真でピュア〜」な二つの運動を見てもらいたい。一つは、「純真でピュア〜」な
子供達が公園のブランコを揺らしている時の動きであり、もう一つは「純真でピュア〜」な「オッパイ星人」達が眺めているGカップバストを揺らす女性の胸板の動きである。
子供達が公園のブランコを揺らしている時の動き
| 「オッパイ星人」達が眺めている Gカップバストを揺らす女性の胸板の動き
|
この二つの図をじっと眺めてみると、何か共通点が見えてはこないだろうか?少なくとも、私(純という名前を持つ位だから純真さでは保証付きである)と同じく「純真でピュア〜」な目で眺めてみれば、共通点が見えてくるハズなのである。
「何か、単に両方グニョグニョした動きにしか見えないぞ。」という人、つまり「純真でピュア〜」な目を持たない人もきっと多いことだろう。哀しいことに、この世知辛い世の中ではそんな「純真でピュア〜」な目を持ち続けるのはムズかしいことなのである。そこで、そんな不純な人でも判りやすいように、さらに
- 子供がブランコを動かすときの「子供の上下方向および水平方向の動き」
- 女性が歩くときの「女性の胸板の上下・左右方向ぞれぞれの動き」
重心の上下方向への運動  |  |
そして、こちらが女性が歩くときの「女性の胸板の上下・左右方向ぞれぞれの動き」である。
胸板の上下方向への運動  | 胸板の左右方向への運動  |
こうしてみると、ブランコを揺らす子供の動きと、Gカップバストを揺らす女性の動きが、よく似ていることがわかるだろう。上下方向への運動は全く同じであるし、左右方向への動きはタイミングが違うだけ、つまり位相が違うだけなのである。その位相の違いを実感するためには、
- 時間
- 左右の動き = X
- 上下の動き = Y
 |  |
方向性が逆であるだけで、全く同じであることがよく判ると思う。方向性の違いを除けば、ブランコを揺らす子供の動きとGカップバストを揺らす女性の動きは全く同じなのであって、私はこれら二つの運動の根本原理は全く同じものなのではないか、と思うのだ。もちろん、その原理を「純真でピュア〜な心」である、と言ってしまえばそれで終わってしまうわけなのだが、それでは「科学(?)」ではない。「純真でピュア〜な心」がブランコを動かし、世界を動かし、ついにはGカップバストを動かしているのだぁ、と言えば哲学的(?)ではあるが、科学(?)ではない。いや、そんなのは科学的でも哲学的でもなくて、単なるエロ・エロ・トークだと言う人もいるかもしれないが、そういうことを言うヤカラは「純真でピュア〜」な目を持たない人に違いないのである。少なくとも、「なんて素晴らしいファンタジ〜なんだぁ」という位には言って欲しいのである。
ただ、「ブランコを揺らす子供の動きとGカップバストを揺らす女性の動きは方向性が逆がである」ということは実は面白い考察ができるのである。前回、ブランコの動きを考えた時に、ブランコの効果的な漕ぎ方と方向性が逆の「ブランコが下にきたあたりで座り込み、ブランコが上にきたあたりで立ち上がった場合 」のシミュレーション計算をしてみた。その結果は、ブランコの振動がどんどん小さくなってしまったのであった。つまり、除振効果が働いてしまうのである。
ということは、である。Gカップバスト(いやAAAカップでも同じであるが)を揺らす女性の動きは、実は揺らしているのではなくて、Gカップバストを揺らさないために最も効果的なのではないだろうか?Gカップバストが揺れ動いてしまってはオッパイ星人はともかく、本人はとても困るわけでそのために実は彼女らは「パラメータ(パラメトリック)励振」という物理現象・科学を応用しているのではないか、と想像してみるのもオツなものではないか、と私は思うのである。
もちろん、ブランコの動きが実は結構複雑であるの以上にGカップバストの動きは複雑である。弾性・塑性・そして様々なブラジャ〜による拘束条件も解明しなければならないだろう。それは実にメンド〜な試みではあるが、きっといつか「純真でピュア〜な心」を持つ学生諸君がその謎を解明するに違いない。「天使のブラによる拘束条件とGカップバストのパラメトリック励振」なんていうタイトルの論文を近日中に目にすることができるに違いない、と私は夢見ているのであった。


