2001-04-07[n年前へ]
■スカートの力学 予習編 
風に吹かれるスカートは
四月になって、春風が強く吹き始めた。春風と言えば聞こえは良いけれど、コンタクトレンズを使っていたりする人は強い風が吹くとゴミが入ったりしやすくて辛いだろうし、まして花粉症だったりすると涙が止まらなかったりしてきっと辛いことだろう。そんな辛い季節でも、たまにドキドキするような気持ちになる瞬間がある。もちろん、それは春風にスカートが舞い上がった瞬間だ。スカートが風に吹かれた瞬間に、私は理由もなく(いや理由はちゃんとあるのだが)心と体がドキドキする。それはもちろん私だけでなくて、男なら間違いなく誰しもがそんなドキドキを味わったことがあるはずだ。もっとも、そんな男心を理解しないヤカラはそんなドキドキを軽蔑するに違いないのだが、それが男というものなのだからしょうがないのである。
とはいえ、男心は「男の心」という位だから、女性にはなかなか判りづらいことだろう。「女子高生なんかはどうせスカートの下に短パンを履いているのに、それでもドキドキするものなの?」などと言う女性も多い。しかし、「それでもドキドキしたりする」ものなのである。いや、もちろんスカートの下にジャージを履いてるなんてもっての他ではあるが、短パンくらいならドキドキ度は全然減らないものなのである。それが、つまりは男というものなのだ。
そして、逆に「スクール水着の秘密」ではないが、女性には常識でも我々男には全然判らないことが世の中にはたくさんあるに違いない。ちなみに、私にとってはスカートもその一つである。何しろ、あまりスカートについて自分のこととして考える機会がなかったのである。いや、実際のところそんな機会は全然無かったのである。そこで、今回は「春風に吹かれるスカート」について考えてみることにした。(本題に入る前に一応書いて置くけれど、今回も「スクール水着の秘密」と同じく、女性から見たら「なんて当たり前のことを」とか「それちょっと違うんじゃないの」ということを書いている。そんな風に感じた方は是非、メールででも私に情報でも頂けたら、と思う次第である。)
| さて、本題である。 この右の図のような「風に吹かれながら女性がスカートを押さえている風景」をよく見かける。もっとも、「よく」見かけるなんていうと、私がさぞそういう風景を探し求めているように聞こえるかもしれないが、そんなことはない。風が強い季節であれば、そんな風景は満ちあふれているのである。 さて、この女性のスカートのように風に吹かれたスカートについてちょっと考えてみよう。
| 女性がスカートを押さえている風景」 (animeBODY)  |
まずは、体の前方から強い風が吹いているものとする。つまり、強い向かい風が吹いている状態である。ちょっとその女性にとってはツライ状態である。そこで、うすみどり色のスカートを履いている女性は、スカートがめくれ上がらないように、スカートの前部を両手で膝近くで押さえているわけだ。しかし、それでも風に吹かれてスカートの後ろは舞い上がってしまう。例えば、下の右図で女子高生の体の後ろでスカートがめくれ上がっている。それをもっと単純にしたのが左で、この図中ではスカートはCの位置まで上がってしまっている。
 |  M.H.Tさん画 |
もちろん、男心からすればCどころではなくて、Aくらいまでスカートには高く高く舞い上がって欲しいわけであるが、女心からすればそれはとんでもない話だろう。
さて、このスカートのめくれあがる位置Cは何で決まるだろうか?もちろん、流体力学・弾塑性体力学などを総動員して解かなければならないわけではあるが、それは次回以降のお楽しみということにしておいて、予習編の今回は単純にスカートがOC方向には曲がらないものとしてみよう。だとしたら、話は簡単だ。ただスカートの裾の広さでCBの長さは制限されるわけである。スカートの裾が広ければ、スカートの端は高くまでめくれあがってしまうし、スカートの裾が狭くなっていれば、スカートは比較的低いところまでしかめくれない。
だから、この下の色々なスカートの中でプリーツ・スカートのようなフレアタイプの場合は、スカートは高隈でめくれ上がってしまうだろうし、タイトスカートのようなスカートの裾が狭いものであれば、強い風にも負けず、スカートはめくれ上がることはないだろう。
プリーツ・スカート
|
|
|
|
しかし、しかしである、スカートの裾を狭くすれば春風にスカートが舞い上がってしまうことはなくなるかもしれない。だけど、スカートの裾の長さが制限するのはスカート自身だけでない。スカートを履いている女性の動き自体も制限してしまうのである。それではずいぶんと窮屈になってしまうことだろう。スカートの裾が狭いせいで歩幅も狭くなって、走り回ったりすることもできなくなるに違いない。だからこそ、脚を蹴り上げる藤原紀香のJ-PHONECMのスカートも、脚の動きが制限されないように、スカートの後ろに切れ目が入っているのだろう。
ということは自由に駆け回ったりしようとすると、つまり、スカートが足枷にならないような裾の広いスカートを履いていると、そんなスカートは風に吹かれて舞い上がりやすいわけだ。そして、そんなスカートを履いていると春風に困らせられることになる。
とはいえ、実際にスカートを履いたことがあるわけじゃないから、私には実際のところよく判らない。だから、女性の方々の「本当はこうなのだ」という教えでも請うしかないのである。結局、スカートの話は、スカートを履く人には常識きわまりない話だろうが、私はこれまで考えたこともなかったので全然よくわからない。これが、男と女の常識の違いなのかもしれない。いや、単に私の常識知らず、という可能性が一番大ではあるのだけれど…
そういえば、辞書でskirtを引いてみると「女;女の子」なんていう風にも書いてあった。なるほど、風に吹かれるスカートも走り回るスカートも、確かにその女性そのものなのかもしれないなぁ、と少しばかり思ったりしたのである。だとしたら、風に吹かれるスカートは向かい風には負けないで欲しいな、と柄にもなく思ってみたりするのである。ホントに私の柄じゃないのだけれど。
2001-07-25[n年前へ]
■遠い空のはて? 
地平線の向こうに手を伸ばせ
先日、富士山の五合目へ行った。と一言で言っても、富士山の五合目にも色々ある。何しろ上り口が、第一人気の「吉田口・河口湖口」、下りの「砂走り」で有名な「御殿場口」「須走口」、そして測候所の白ドームを目指し最短距離一直線の「富士宮口」と四種類もあるのだ。その色々ある五合目の中で、先日私が行ったのは富士宮口の五合目というところだ。富士山の太平洋側から富士山頂に向かう登山口の標高2400m地点ということになる。もしかしたら、表富士五合目と言う言い方のほうが有名なのかもしれない。
その表富士五合目から下を眺めると、ずいぶんと遠くまで見えることに本当に心からビックリした。雲が下のほうに広がっていて、そしてその向こうに海や山や地平線が見える。そして、気のせいか地平線がとても丸いような気がする。その五合目までは車で簡単に来ることができたのだけれど、さすが標高2400mは伊達ではなかった…。やっぱり富士山は日本一の山かもしれない…。そして、そんな景色を眺めているうちに、私は色々考えてしまった。
あぁ、下を眺めると遠くまで景色が本当にきれいだ。そういえば、眺めると言えば…これまで、私は急な階段の下から上を眺めたらスカートの内側の下着なんかを覗けるかどうかをジックリ考えてみたりしてきたなぁ。それに、SONYの誇る可愛いらしいAIBOの気持ちになって、やっぱり同じく低いAIBOの視点から上を見上げたらやっぱりスカートの内側が覗けるかどうかを考えてみたりしたなぁ。見上げてばっかりだなぁ、しかも、どれもスカートの内側かぁ…。
そういえば、透け透け水着もマズかったなぁ…。あれ、本当に仕事の話から始まったんだけどなぁ…。誰も信じてくれないし…。あぁ、だけど、やはりそんなことを考えていてはいけなかったんだ…。そんなことをしてたから、画像処理追求サイトを目指したハズだったのに、何時の間にか有害サイト認定されてしまったりしたに違いないんだ…。ついには、「こどもに見せられないページ」保証までされたりするしなぁ…
私は一体何処で間違えてしまったのだろう…? あぁ、それにしても地平線がきれいだ…。地平線が丸い…。 あぁ、地球はやっぱり丸いんだなぁ…。
と、まるで「生きる」で「ブランコに乗りながら人生を振り返る」志村喬のように、我が身を振り返っている内に、ふと「そういえば、地平線って一体どのくらい向こうにあるんだっけ?」と考えはじめてしまった。そもそも、地球が丸いからどうしてもある距離以上は見通すことができなくて、それが地平線なわけだけど、それは一体どのくらい先なのだったのだろうか?
おぼろげな記憶を辿ると、意外に地平線は自分の近くにあって、確かほんの数km先程度だった気がするのだけれど…。さて?あれ? はて… 果て…?
というわけで、地平線までの距離を計算してみた。まずは、そのために下図のように視点の高さYと地球の半径Rをとってやる。
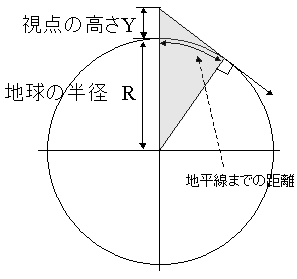 |
「視点位置」と「地球中心」と「地平線」を結んだ三角形(グレーで塗りつぶした部分)がもう簡単なくらいに直角三角形なことに注目して解いてみると、「地平線までの距離」は「視点の高さY」の関数として
というような形になる(計算が合ってれば…)。これに、地球の半径R = 6400kmを代入してやれば、視点の高さYに応じた地平線までの距離が求められるわけだ。
そこで、まずは視点の高さが0〜3m位までの場合をグラフにしてみたのが次の図である。歩き始めて広い世界で暴れだすだろう頃の一才児の身長を緑○、そして、かつてはデカイの代名詞といえばコイツという存在だったアンドレ・ザ・ジャイアントの身長223cmを青○で記入してみた。
青:アンドレ・ザ・ジャイアントの身長 = 223cm  |
このグラフを見ると、一才児の地平線はおよそ3km先にあって、アンドレ・ザ・ジャイアントの地平線は5〜6km先にあることがわかる。もちろん、その間の身長の人達の地平線はその中間、そう4km先くらいにあるわけだ。私たちの地平線はほんの4km先、なんと走ればほんの20分位のところ、歩いても一時間かからない程度の近くに地平線はあるのだった。地平線なんていうと、遥か遠くにあるように思えるけれど、手の届くほんのすぐ先にいるのである。
そして、歩き始めた子供の地平線と巨人アンドレ・ザ・ジャイアントの地平線がたいして変わらない、というところも面白いものだ。あれだけ背が高ければ、さぞかし広い世界を眺めているのだろう、と思ったりするがそういうわけでもないのである。
じゃあ、もう少し高い場所に行くとどうか、ということで1000mまで視点の高さを上げてみたのが次のグラフである。東京タワーの特別展望台の250mを緑○で、あくまで計画中の秋葉原タワーの特別展望台の500mを青○で示してある。 ここまで上がると、250m地点で地平線は60km先になり、500m地点では80km程度先まで見通せることになる。東京駅の位置からの距離で言うと、60kmでは箱根くらい、80kmで三島くらいだろう。
青:計画中の秋葉原タワーの特別展望台 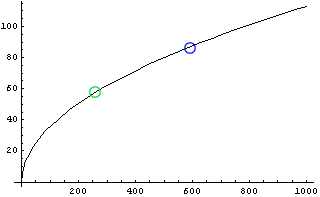 |
調子に乗って、さらに視点を高くしてみよう。先の表富士の五合目2400m地点では200km近く見渡せ、東京駅からの距離で言うと地平線は遠く浜名湖辺りまで離れていく。そして、さらにさらに視点を上昇させ、ジャンボジェット機の巡航高度地上10kmからであれば、なんと350kmほども見渡せるのである。350kmだと東京駅から京都くらいだろうか。東京-京都と言えば、そうちょうど東海道五十三次だ。江戸時代の人達が一月近くもかけて歩いたくらいの彼方まで地平線は後ろへ下がっていくわけだ。地平線は時が流れるにしたがって、遠くに広がっていくのだ。
青:ジャンボジェット機の巡航高度 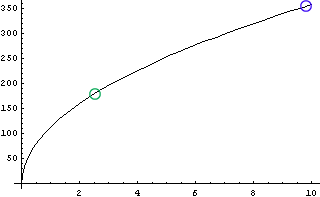 |
そのジャンボジェット機から見える地平線は、かつては一月近くもかけて歩いたくらいの遠く、400kmも遠くなのだから、そこまで行くと地平線が「遥か遠く」に思える。一瞬そう思える、のだけれど実はそんなことはない。ジャンボジェット機の速度からすれば、そんな遥か彼方の地平線だって、やっぱり30分ちょい位のすぐ近くだ。私たちが普通に立っているときの地平線が4〜5kmくらいのすぐ近くにあって、歩いてみればやっぱり30分ちょいで行ける、というのとほとんど同じなのだ。

ジャンボジェット機から眺めた地平線(水平線)
五歳くらいの子供の地平線と、空を飛び回るジャンボジェット機の地平線を時間を距離の単位として比較してみれば実はほとんど同じ遠さだ、というのは何だかとても面白い。大地の果てと天とが接っする地平線はとっても近くにあって、そこまで行くのにかかる時間は小さな子供でも巨大なジャンボジェット機でも同じなのである。
「地平線」なんて言うと、まるで「手が届かないもの」の代名詞みたいに使われたり、あるいは「その先には何があるのかわからないもの」の代名詞に使われたりするけれど、ちょっと行こうとして見れば、片道30分ちょっとでその「地平線」まで辿りつくことができるわけだ。案外、遠くにあると思い込んでいるものも、手を伸ばしてみれば、もしかしたら手が届くものなのかもしれない。しかも、それは地平線まで辿り着く時間が小さな子供でも巨大なジャンボジェット機でも同じだったように、誰でもできたりするものなのかもしれない。
もちろん、かつての「地平線」だった場所まで辿り着いたとしても、新しい「地平線」は視界の向こうに下がって行くわけなのだけれど、そこまでだってやっぱり歩けばほんの30分だ。遠い空の果て、地平線の向こうは、すぐそこだ。
2001-08-07[n年前へ]
■「ボケ」た背景で包み込め 
デジカメ画像をキレイにボカそう アルゴリズム編
最近、新しいデジカメを物色中である。私はこれまではFinePix4700zを使っていたのだけど、そのFinePixが半年程度で壊れてしまった。というわけで、C-4040ZOOMがどんなものか期待しているところである。
壊れたFinePixと言えば、そもそも壊れたFinePixは一台ではなかった。私はすでにFinePixを二台も買っているのだ。そして、もうすでに二台とも壊れてしまっているのである。連続殺人事件ならぬ、連続カメラ自殺事件なのである。
まず、一台目に買ったFinePix700ははメキシコのティファナでポケットから落としたら、バッテリーから電源が供給されなくなった。もちろん、ACアダプターを使えば立派に動くのだけれど、それでは少しばかり機動性に欠けてしまう。まさか発電機を持ち歩くわけにはいかないし、コンセントの近くでしか撮影することができないとなると、それは非常に困ってしまう。そこで、すかさず二代目としてFinePix4700zを私は買った。ところが、買ってから半年位たったある日、今度は勤務先の駐車場でポケットから落としてしまった。すると、今度はファインダー視野がズームに連動しなくなって、なおかつレンズがまるでジョイスティックのようにあらゆる方向に曲がるようになってしまった。
こんな風にデジカメはとっても壊れやすくて、半年毎にデジカメ出費を強いられる私に周囲は「落としたオマエが悪い」と非常に冷たいのである。残念なのだ。「そういうのは壊れたんじゃなくて、壊したんだ」と被害者である私をまるで加害者のように告発する人さえいるのである。連続カメラ自殺事件は実は他殺で、しかも犯人は私だと告発する輩さえいるのだ。ひどい話である。
ところで、C-4040に期待しているのは、コンパクトで、レンズアダプターが使えて、レンズがF1.8と明るいことなのである。コンパクトなのは持ち歩くために必要だし、私はなんと言っても超広角デジカメが欲しいのだが、そんなデジカメはないので、ワイドコンバーターを付けたいのでレンズアダプターが必要なのである。明るいレンズの方は、うす暗い中でも撮影する時に重宝しそうなので、少し期待しているのである。
ところで、この位明るいレンズであれば、もう少しぼかすことができるものだろうか?デジカメで写真を撮ってもどうしてもボケない。35mmフィルムを使っているカメラなどと比べるともう全然ボケない。もうほんとにボケない。
例えば、35mmカメラで135mm F4.5開放のレンズなら、ピントの合ってない背景はこの位はボケる。これは京都の哲学の道近くにある吉田山で撮った写真だ。
 |  |
ピントが合っている位置以外は光がボケて、キレイなボケが発生する。どちらの写真も絞りは開放で撮影しているので、後ろの風景はほぼ丸くボケている。ぼかせばキレイというわけではないけれど、背景などがごちゃごちゃしている中で対象物だけを浮き上がらせたい場合には、「ボケ」させるととても良い感じになる。
しかし、デジカメではそうそう簡単にボケた画像を撮影することはできない。35mmフィルムに比べて、CCDサイズが小さいからである。35mmカメラよりAPSカメラはもっとぼけなくて、それよりデジカメはさらにボケないのである。そんな様子を見るために、二台目として買ったFinePix4700zで「ボケ」を意識して撮影してみたものが下の写真である。手前の植物にピントが合って、奥の道の先はボケてはいるのだけれど、それでも先程の写真などとは比べものにならないほどわずかしかボケていない。
 |
ところで、このような画像の「ボケ」を考えるとき、「ボケ」た画像をシャープに復元しようという話は非常にポピュラーな話題である。例えば、本「できるかな?」でもこれまでに
といった感じで遊んできた。また、さらには「恋の形」を復元しようとしたとか、このようなアプローチを遥か昔に考えていた漱石の「文学論」を振り返ってみたりしたきたのである。しかし、これらはいずれも「ボケたデータを復元する」という問題であった。一方、この逆のアプローチである「シャープなデータをボケたデータにする」という問題も結構ポピュラーである。例えば、音楽をホールやライブハウス風にボケた音にするDSPはかなりの数のオーディオ装置に付けられている。これも、もともとはシャープな音声データが部屋の中でボケていく様子をシミュレートする回路である。また、画像に関する話題でも、ピント位置をずらした複数の画像から任意の「ボケ」画像を作成するといった話題もたまに見かける。
そこで、「できるかな?」でもデジカメ画像を35mmカメラ風にキレイにぼかすことに挑戦してみることにした。今回は、まずはアルゴリズムを確認して、次回以降で簡単プログラムを作成してみることにしたい。
まずは、似たようなソフトウェアがあるかどうか、Googleで適当なキーワードを使って検索をかけてみると、IrisFilter(http://www.reiji.net/iris/)というソフトウェアがあった。これは、「写真のぴんぼけを再現する」というフィルターだった。サンプル写真などを見てみると、これがなかなかきれいだった。例えば、早朝の御殿場の路上を「在りし日のFinePix4700z」で撮影した写真にこのフィルタをかけて、「ボケ」を加えてみたのが下の画像である。
 |  |
ここではこんな![]() 六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
WEBページの記載によれば、このIris Filterは「フィルム特性曲線を利用し、レンズから通った光がフィルムを感光させる様子を再現しています」ということである。なんでも、特許も国内・USP共に出願済みということだが、特願2000-100042もU.S.PTO 09/772532も未だ公開にはなっていないようで、残念ながら特許の内容を読むことはできなない。
このWEBページの記述の中で面白いのは、「データ上の数値をそのまま拡散させる従来のPhotoshopをはじめとした画像処理ソフトと違い、実際のフィルムに当たる光の量(露光量)を逆算し、その露光量をもってピントがずれている様子を再現します」という歌い文句でPhotoshopの「ガウスぼかし」と比較広告してある部分である。
試しに、先の画像をIris Filterで「ボケ」を加えた画像と、Photoshopの「ガウスぼかし」とで「ボケ」を加えた画像を比較してみると、下の二枚の画像のようになる。確かにIrisFilterの売り文句通り、こうして比較してみるとPhotoshopガウスぼかしが写真の「ボケ」っぽくないのに対して、IrisFilterの「ボケ」が写真のそれっぽいことが良くわかる。
 |  |
さて、お仕着せのソフトを使ってみるだけではなくて、自分でデジカメ画像をキレイに「ボケ」させてみることにしたい。というわけで、hirax.net風「ボケ」フィルターの動作を考えてみる。
まずは、毎度のことだがオリジナル画像が「ボケ」る様子を計算する式は
逆フーリエ変換( フーリエ変換( オリジナル画像 ) x フーリエ変換(ボケ具合 ) )と表すことができる。詳しくは、「宇宙人はどこにいる?」の回でも読んでもらうことにして、簡単に言えば周波数領域でオリジナル画像とボケ具合を掛け算をしさえすれば良いのである。つまり、今回のデジカメ画像をぼかす場合だったら、
- デジカメ画像と「ボケ」具合をそれぞれフーリエ変換し周波数空間に変換
- 周波数空間で乗算を行う
- 逆フーリエ変換して実空間に戻す
じゃぁ、早速やってみようとなるわけだが、その前にもう一つ注意することがある。それは、RGB画像の数値というものは実は元々「明るさを対数変換した値」であるということなのである。人間の目も含めて世の中の大抵の材料は対数的な感度を持っている。例えば、人間の目に「2倍明るい」という場合に、光は「2倍明るい」というわけではない。その場合には指数的にX^2倍明るいのである(ここで、xの値はそれぞれのデバイスによって色々と違う)。その明るさをRGB画像の数値データにする時に、明るさの対数をとってLog[x,X^2]で2という数値として表しているわけだ。
RGB画像の数値が「明るさを対数変換した値」だというようすの一例を示すと下の図のようになる。
横軸 = 0〜255の数値データ 縦軸 = エネルギー  | 横軸 = 0〜255の数値データ 縦軸 = エネルギー  |
逆に明るさからRGB画像の数値データへの変換グラフは例えばこんな感じである。RGB数値で200と255と言っても実はその明るさは大違いであることがわかると思う。
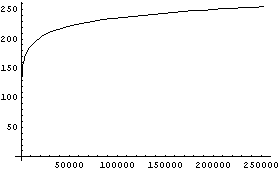 |
だから、この手の処理を行う際には、まずは指数変換してから処理を行い、そしてその後対数変換してやらなければならないわけだ。もちろん、今回のデジカメ画像をぼかす場合にも、RGB画像の数値をまずは指数変換した後、「ボケ」演算を行って、その演算結果を対数変換でRGB画像の数値に戻してやらなければならないのである。といっても、別に難しい話ではなくて画像を扱う装置だとごく当り前の話だ。
そう、「ボケ」演算のhirax.net風レシピはたったこれだけ〜というわけで、早速このレシピに従ってhirax.net風デジカメ「ボケ」フィルターをかけてみたのが下の画像である。キレイな「ボケ」画像ができあがっていることが判ると思う。
 |
ところで、デジカメ画像のRGB画像の数値を指数変換したものに「ボケ」演算を行ったわけだけれど、もしRGB画像の数値そのものに対して「ボケ」演算を行ったら、どんな結果になるだろうか?つまり、「データ上の数値をそのまま拡散させる」やり方をしたら、どうなるのだろうか?そこで、試しにRGB画像の数値そのものに対して「ボケ」演算を行ってみるとこんな結果になる。
 |
何だかボンヤリとにじんだだけの「キレイじゃない」写真になってしまっている。それは、当り前である。本来2倍明るいものはX^2倍明るいわけで、すごく光の量は2倍どころでなく多いわけだ。それが広がる量を仮にRGB数値そのまま2倍として扱ってしまうと、その光の部分は薄暗くなってしまう。コントラストのはっきりしない、ぼんやりとした写真になってしまうわけだ。ちゃんと、X^2倍のデータとして扱ってやらなければならないわけである。
試しに、指数処理したものと線形処理をしたものとを並べてみるとその画像の違いがよくわかるだろう。
キレイなボケ画像(指数処理)  | キレイじゃないボケ画像(線形処理)  |
さて、今回はデジカメ画像の「ボケ」フィルターのhirax.net風レシピを確認してみた。次回(と言ってもいつになるか…)以降に、このレシピに従って実際にソフトを作成していこうと思う。
ところで、「文学論」の中で漱石は「ボケ」は焦点的印象又は観念に付随する情緒を意味する、と言っている。それは、言い換えれば「何かの出来事をきっかけとして感じた怒り・悲しみ・喜びなどの感情がボケである」ということだ。そして、さらに言えば、写真で背景をぼかすということは、つまり「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて包み込む」ということなのである。
だから、何かを撮影する時に対象物の背景をぼかすということは、「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて対象物を包み込んで、そして対象物を浮き上がらせる」ということなのかなぁ、とぼんやりと考えてみたりする。そんな写真は対象物を写しこんでいるのと同時に、それを包みこむ背景も写しこんでいるンだろうなぁ、と考えてみたりする。

2001-08-13[n年前へ]
■二年ぶり?の山小屋 
謎のリスが布団から飛び出してきたり、大量に買ったビールと食べ物があっという間になくなって、結局店まで三往復したり、小屋ではNTTドコモはOKなのに、CdmaOneは圏外で悔しかったりの一日。
こんなみどりに囲まれた生活(最低限のネットワーク環境付きで…)もしてみたいなぁ。(リンク)(リンク)(リンク)
2001-10-08[n年前へ]
■廊下に立たされた男… 
テロの影響で某年中行事が中止なので、10月前半のいつもの東京出張は中止になってます。数年前の「まるで廊下に立たされている中学生のような」わき・ひがしペアーが懐かしいです
でもって、先週の「席替え」の結果、私の左隣「く」さん、右隣「い」くん、真後ろ「ロボすずき」さんになりました。ひがしさんは「ロボさん」の左二つ隣です。こんなカタチのご報告もアリですよね?本来なら、美少年でご報告したいどころなのですが、新鮮なうちにということで、ここで…。
とりあえず、色々動いた半年でしたが、なにはともあれありがとうございました。とはいえ、これでやっと"Starting Over"といったところです。



