1999-05-30[n年前へ]
■パーマンのパラドックス 
ボトルネックは何処だ?!
以前、
ハードディスクのエントロピーは増大するか?- デフラグと突然変異の共通点 - (1999.03.28)
の最後に「突然変異(あるいは、ハードディスクで言えばデフラグメント)のような現象が起きて、エントロピーが減少しない限り、熱的死(いや企業や会社であれば画一化、平凡化、そして、衰退だろうか)を迎えてしまうのだろう。」と書いた時に少し不思議な感じがした。それは、次のような矛盾を感じたのである。
まずは、
- 何事につけても、全体としての強さは一番弱いところで決まってしまう。
- 全体としての完成度を高くするためには、どこの強さも同じであるのが理想的である。
- 従って、全体を構成する部分というものは均質であるのが理想的である。
もし、ビルの鉄骨の一部に弱い所があれば、そこから崩壊が始まり、いずれビルが崩壊することは免れないだろう。
精度・力が高い所がいくらあろうと、「一番精度・力が低い所の=全体の精度・力」なのである。従って、一番精度・力が低い所を改良するのが全体としての完成度を高めるための唯一の方法である。
これは、モノであろうが、個人であろうが、グループであろうが同じである。例えば、写真を撮って出力することを考えよう。いくら写真の素材が良くてもカメラマンの腕が悪ければ駄目であるし、写真自体が良くても、写真の出力装置が悪ければ、それもやはり駄目である。そもそも、カメラマンが狙う被写体自体が悪ければ、答えはやはり同じである。
従って、精度・力を揃えた均質的な状態でなければ良いものは生まれないわけである。
これと、先の「画一化、平凡化、そして、衰退」すなわち、「画一化は良くない」ということの間に矛盾を感じたわけである。
しかし、少し考えてみると特に矛盾が無いことがわかる。ロボットを作る場合を考える。
- まずは一人で機械系も電気系もソフト部分も自分で作っていた。
- ソフト部分がどうも苦手なので、ソフトが得意な友達に手伝ってもらう。
- すると、電気系が比較的うまく行かないようだ。
- そこで、友達の友達に電気系を手伝ってもらう。
- それぞれ得意な部分で力を発揮し、特に弱いところもなくなった。
- ロボットの完成だ。
それでは、数学的にふざけたことを考えてみる。といっても、難しく考えるのではなく、中学生でも知っていそうなあの式を使うのである。
簡単の為にX,Y二つの部品からなるものを考える。それらの単独での精度(あるいは、出力)をx,yとすれば、全体としての精度(あるいは、出力)を考えると、それは(x* y)^(1/2)と置くのが自然だろう。それぞれ単独であれば、単なる和としては(x + y)/2であるわけである。ここで、2で割ったり1/2乗しているのは規格化しているようなものである(あとの落ちに繋げるためでもあるのだが...)。
今やりたいことは、(x * y)^(1/2)がなるべく大きくなるようにしたいのである。というわけで、相加相乗平均の関係式の登場である。
| x->(0,50),y->(0,50)の範囲で図示したもの | |
| (x+y)/2 ...相加 |  |
| (x * y)^(1/2) ...相乗 |  |
| (x * y)^(1/2)-(x + y)/2 ...相乗-相加 |  |

すなわち、x=yの時に(x * y)^(1/2)は最大になるわけである。良く知られている、相加相乗平均の関係式である。今回の話では、それぞれの精度・力が均質であれば理想的というのはこういったことである。異なる分野・方法で力を発揮しという方は簡単だ。異なる分野・方法で力を発揮するのでなければ、わざわざ乗算、すなわち、いっしょに組ませる必要がない。
さて、タイトルの「パーマンのパラドクス」であるが、少々疲れてきたので、本題は次回にしたい。今回はタイトルについての考察を上の話に絡めてしてみるに留める。
私は「パーマン」についてほとんど知識がない。TVアニメを観ていた記憶がある位である。だから、パーマンの名前の由来が何であるか知らない。スーパーマン+罰としての「パー」からきているのかもしれないが、ここで勝手な想像をしてみる。英語で考えてみると、par=同等、同水準、平均であるから、par-manは「平凡な主人公ががんばってスーパーマンになる」という気持ちが込められているのかもしれない。これはありそうな話である。
ここで、「平均」でなくて同等というような意味をそこに入れたらどうなるだろうか?パーマン1,2,3,4号に対して、par=同等、同水準、平均というような視点から考えてみるのである。あるいは、パーマンだけではなく、他で考えたらどうだろうか....
1999-08-14[n年前へ]
■年始は景気が悪いの法則 
株価・為替グラフ表示ソフトを作ろう
自慢ではないが、私は経済には疎い。しかし、霞を食べて生きているわけではないので、勤務先の景気の行方は私の食生活を左右してしまう。その年の給料は年始に労使交渉の後に決まるのだが、何故か毎年その時期は勤務先の景気は悪いのである。当然、毎年不景気な労使交渉が行われることになる。
「何故か毎年その時期は勤務先の景気は悪い」と書いたが、わかっている理由もある。例えば、その前年末に売れてない製品を売れたことにして前年の売上に押しこめてしまうから、次の年始は当然製品の売れ行きが下がるわけである。従って、給料を安く抑えるためには、労使交渉を年始に行うのがいいと思われる。
そういうことはおいておいても、経済の勉強は少しはしなければならないだろう。こう思ったきっかけは、「今日の必ずトクする一言(http://www.tomoya.com/)」の
- 株価の先読みは可能か?(風水学的に店頭市場を見る編)
- (http://www.bekkoame.ne.jp/~jh6bha/higa9904.html#990427)
それでは、今回のサンプルには「カシオ計算機(株)」を使うことにしてみる。まずは、カシオ計算機の株価の最近一年間の変動を以下に示してみる。
 |
さて、これだけでは何がなんだかわからないし、カシオ計算機の特徴もわからない。
- 他の会社の平均に対してカシオ計算機の特徴はどうか?
- カシオ計算機の株価と相関があるパラメータは何か?
他の会社の平均を調べるためには、日経平均株価を見れば良いのだろう。そして、カシオ計算機のような輸出を主体とする製造業の場合は、円vsUS$為替が株価と極めて相関が高いことが多いので、日経平均株価と円vsUS$為替の変動を示してくれるサイトがあれば簡単に比較ができるだろう。例えば、そういった情報はYAHOOやASAHI..COMから得ることができる。
しかし、大雑把に探した限りでは、日経平均株価と円vsUS$為替の変動を同時に表示してくれるサイトが見当たらなかった。そこで、日経平均株価と円vsUS$為替の一年間の変動を表示するソフトウェアEconomicを作成することにした(経済の勉強から離れてしまっている気もするが...)。
プログラムの内容はごく簡単で、ASAHI.COMにアクセスして「日経平均株価」と「円vsUS$為替の変動」を示す画像を取得して、合成するだけである。今のところ、proxy対応にはしていないが、そうするのもごく簡単なので、気が向けばproxy対応にするつもりだ。
また、動作のためにはSUSIEプラグインのJPEG対応プラグインを必要とするので「Susieの部屋」から適当なプラグインをダウンロードし、Economicプログラムと同じディレクトリか、システム、もしくはSUSIEアプリケーションのあるディレクトリに入れておく必要がある(経済の勉強をするのに、何故SUSIEプラグインの話になるのだろう? というツッコミは無しだ。)。Economicプログラムは以下からダウンロードできる。
 緑 : 円vsUS$為替 紫 : 日経平均株価: |
- 他の会社の平均に対してカシオ計算機の特徴はどうか?
- カシオ計算機の株価と相関があるパラメータは何か?
それでは、このEconomicを用いて、カシオ計算機の株価の変動を見てみよう。
 |  |
見比べてみると、カシオ計算機の株価は日経平均株価(左の紫の線で示してあるもの)とはあまり相関が無い。日経平均株価が右上がりで高くなっているのに対して、カシオ計算機の株価は最初に大きく低下した後に、低迷を続けている。
それに対して、円vsUS$為替の変動(左の緑の線で示してあるもの)と見比べてみると、ほぼ同じであることがわかる。輸出を行っているメーカーはどうしてもこうなってしまう。例えば、1円円高になると為替で数十億円も損失が出たりするのである。素晴らしい製品を作るかどうかよりも、円高になるか円安になるかの方が重要であったりするのだ。しかも、(私の気のせいだとは思うが)いつも年始は円高で、そのため毎年給料が不景気になるような気もするのだ。困ったものである(私が)。
さて、こういったプログラムは作るのが簡単な割に面白い(私としては)ので、色々と応用プログラムを作成して遊んでみるつもりである。そうして、いつか経済オンチを克服してみたいと思うのであった(経済の話なんかほとんど出てきてないような気もするが...)。
2000-05-14[n年前へ]
■恋する心を見てみたい 
恋のきっかけはどの出来事?
まずは、簡単な背景から... 今回の話は
を元に大幅に書き直したものである。少し思うところがあって書き直した結果、まったく別物になってしまった。そこで、ここに登場する次第である。以前の話の場合は、「恋のインパルス応答」という言葉を思いついて、最後におまけのように書いてみたわけであるが、今回はそれをメインに書き直してみたのである。A子:「あのさ、アイツほんと酷い男よ。」
A子:「なんで、あんな男好きになったの?」
B子:「そんなこと言われても、私にだって判るわけないじゃない。」
TVドラマを見ていると、時々こんな会話が流れる。登場人物は二人の女の人、舞台はバーのカウンターや旅先や、とにかく日本全国津々浦々である。そして、話をしている雰囲気は真剣そのものである。きっと、B子は悪い男を好きなっていて苦労しているのだろう。そして、きっとB子の親友であるA子が、悪い男に騙されている「恋する心」で一杯のB子を諭しているところなのだろう。
本当のところ、こんな会話が巷に溢れているのかどうか、私は知らない。そりゃそうだろう。私は男であって、女の人が二人というシチュエーションは全然立ち会える筈がない。じゃあ、同じような会話を私ができるかというと、それもやはりできないのだ。論より証拠、もし私がそんなことを言ったらどうなるだろうか?
私:「あのさ、アイツほんと酷い男だよ。」これは相手が女の人だからで、男なら大丈夫だろう、と言われるかもしれない。しかし、そっちの方が実は質が悪い。
私:「なんで、あんな男好きになったの?」
B子:「そんなこと、何でアンタに言われなきゃならないの?。」
私:「いや、ちょっと…」
私:「あのさ、アイツほんと酷い女だよ。」これはとても危険な会話であることが判るだろう。この後は修羅場が待っているハズだ。あるいは、私は道端に倒れていることになるかもしれない。「小さな親切、大きなお世話」である。根本の原因は私の人間性にあるような気もするのだが、そこは今回は考えないでおきたい。
B男:「なんで、オマエがそんなこと知ってんねん?」
私:「いや、ちょっと…」
さて、最初のB子のセリフ「そんなこと言われても、私にだって判るわけないじゃない。」という会話の真偽はともかく、恋する本人にも恋のきっかけというのは不思議なものなのだろう。そして、本人以外にとっても「恋する心」の揺れ動く様子というものはとても興味深いものだ。
そこで今回は、色々な「出来事・きっかけ」が「恋する心」を変化させていく様子を調べてみることにした。今回の登場人物は、
- A子 : 「瞬間」的に燃え上がるタイプの女の人
- B子 : 「ゆっくり」燃えるタイプの女の人
- C男 : いつも、とっても良い男
- D男 : ほとんどの場合、悪い男
次のグラフは
- 横軸 = 時間軸 左から右へ時間は進んでいるとしておく
- 縦軸 = 「恋する心」の大きさ
 |
「瞬間」タイプの女の人A子の場合、その出来事の前後には「恋する心」が瞬間的に盛り上がる。しかし、それほど持続するわけではないのだ。燃えやすく、忘れっぽいタイプである。芸能人で言うと松田聖子あたりがこの例に当てはまるだろう。
それに対して、「ゆっくり」タイプの女の人であるB子の場合には、「恋の炎」がずいぶんとゆっくり燃え出している。また、「恋する心」の広がりが広い分だけ、「恋する心」の最大値も低くなっている。芸能人で言うと誰になるだあろうか?私にはちょっと思いつかない。
それでは、この 「瞬間」タイプのA子と「ゆっくり」タイプのB子が、いつもとっても良い男であるC男に恋をした場合を考えてみる。まずは、優しいC男は色々なことをするのだ。それが、「恋のきっかけ」となる。
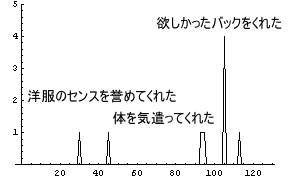 |
時間が左から右へ進んでいくわけであるが、その間にC男は色々なことをするのである。洋服を誉めたり、体を気遣ったり、バックをプレゼントしたり、何ともマメな男である。
また、ここでは「洋服のセンスを誉めたり」、「体を気遣ったり」するという「出来事」よりも、「欲しかったバックをくれた」という「出来事」の方がポイントが高い。ずいぶんと、「即物的」な場合にしてしまった。これなどは、適当にそうしただけで、「私は精神的なポイントの方が高い」という人の方がもちろん私は大好きである。
それでは、これらの色々な「出来事」が起きる時のA子とB子の「恋する心」の変化はどうなるだろうか?先ほど、ある一つの「出来事」に対する「恋する心」の応答を、「恋のインパルス応答」と呼ぶ、と書いた。ある一つの「出来事」によって「恋する心」がどうなるかは、「恋のインパルス応答」を見れば判るわけだ。だったら、色々な出来事が起きた数の分だけ、「恋のインパルス応答」を足し合わせてやれば良いわけだ。この「色々な出来事が起きた数の分だけ、- 恋のインパルス応答 - を足し合わせてやる」という作業を、恋の信号処理では「畳み込み」と呼ぶ。結局、
色々な「出来事・きっかけ」と「恋のインパルス応答」の畳み込み= 「恋する心」という「恋する心」の信号処理が可能なのである。
早速、A子とB子の「恋のインパルス応答」を用いて、先の色々な「出来事・きっかけ」に対する「恋する心」を計算してみた。それが、下のグラフである。黒字がA子、赤字がB子の「恋する心」である。
 |
「瞬間」タイプのA子の場合、ホントに燃え上がるのが早い。C男が洋服のセンスを誉めてくれただけで、もう結構「恋する心」が盛り上がっている。「ビビッ」と恋をして結婚をしてしまいそうなタイプだ。その代わり、一瞬でその「恋する心」が消えているところが怖い。あっという間に離婚をしそうなタイプでもある。
「ゆっくり」タイプのB子の場合は、洋服のセンスを誉められた位では「恋する心」は盛り上がっていない。もちろん、C男に対して良い印象は持ち続けているようだが、恋というほどでもない。
その代わり、A子のように欲しかったバックを貰っても、しばらくすると「恋する心」はすぐに冷める、というようなことはない。C男にとっては、「恋人」になるまでは大変であるが、その後は落ち着いた恋人生活を過ごせそうな相手である。私はC男にはA子よりも、B子の方が相応しいと思うのだが、どうだろうか?(しかし、次回C男には哀しい現実が待ち受けるのであるが...)
さて、このページも少し長くなってきた。そこで、この後は次回に続くことにする。今回、まだ登場していない
- D男 : ほとんどの場合、悪い男
A子:「あのさ、アイツほんと酷い男よ。」という冒頭の会話のような、女の人たちがなぜ数多くいるか(少なくともTVドラマの中では)を明らかにしてみたい。そして、優しいC男の悲しい恋の行方を描いていきたいと思うのである。
A子:「なんで、あんな男好きになったの?」
B子:「そんなこと言われても、私にだって判るわけないじゃない。」
ところで、「辛(つらい)」と「幸(幸せ)」という漢字は互いによく似ている。時々、どっちが「幸せ」だったっけ?と判らなくなりそうになるくらいだ。次回、「恋の印象の平均化効果」というものを武器に、「辛(つらい)」が「幸(幸せ)」にすりかわる様子を見てみることにしたい。「辛(つらい)」が「幸(幸せ)」は紙一重なのだ。「辛(つらい)」は「幸(幸せ)」で、「幸(幸せ)」は「辛(つらい)」なのである。
2000-05-17[n年前へ]
■恋の形を見た人は 
恋の相対性理論
さて、前回
では、三人の登場人物A子 : 「瞬間」的に燃え上がるタイプの女の人達の間で繰りひろげられる色々な「出来事・きっかけ」と、それにより発生する「恋する心」を「恋のインパルス応答」を用いて計算してみた。その結果、C男とB子がカップルになれば「ほのぼの」とした幸せな生活をしそうだ、というところまで考察した。
B子 : 「ゆっくり」燃えるタイプの女の人
C男 : いつも、とっても良い男
今回は、その三人に加えて
- D男 : ほとんどの場合、悪い男
さて、今回登場する「D男 = ほとんどの場合、悪い男」はかなり酷い男である。D男がA子とB子に対して何をしたか時系列を追ってみてみることにしよう。
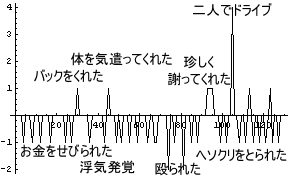 |
- お金をせびり、
- 浮気をするし、
- それを追求すると殴る蹴るの暴行を働き、
- せっせと貯めたヘソクリを奪いパチンコに行ってしまう、
それに対して、前回のC男は次のグラフのように悪いことは何一つしない良い男だ。
 |
悪いことは何一つしない。良いことばかりをしてくれるのである。何とも良い人である。普通に考えれば、女の人の「ハート」はC男ががっちり掴み、D男は警察官にでもがっちり掴まれているのが当然であろう。掴まれたが最後、シャバには二度と出てきてこないで欲しい位である。しかし、そう単純な話ではないのだ。
人の感覚には「順応」というものがある。簡単に言えば「慣れ」である。ひどいことしかしない男と普段接していると、それが当たり前に思えてしまうのである。相対化してしまうのだ。普段のD男に対する印象が「当たり前」に思えてしまうのである。
さて、その「恋する心」の「順応」を計算するにはどうしたら良いだろうか?そう、普段の印象を基準にすれば良いのだ。普段の印象、すなわち「印象の平均値」を「恋する心」から引けば良いのである。例えば、A子のC男に対する「恋する心」を計算してみることにする。次のグラフで黒字が「色々な出来事」と「恋のインパルス応答」の畳み込みであり、本来のあるべき「恋する心」である。そして、緑字が環境順応後、すなわち、本来のあるべき「恋する心」から「印象の平均値」を引いた「恋する心」である。
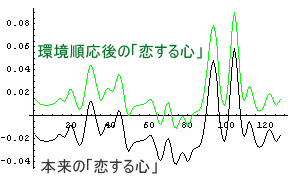 |
この図で、環境順応後の「恋する心」が本来の「恋する心」よりいい印象であることがわかると思う。何故かというと、環境に順応するということは普段の印象が当たり前の状態と思ってしまうことである。普段「悪い」男を相手にする場合は、「悪い」のが当たり前だと思ってしまうのである。数学的には、「悪い」のを引くのであるから、「マイナスを引くとプラスになる」のと同じである。それを式で表してみると、
環境順応後の「恋する心」 = 本来の「恋する心」 - 普段の態度
なのであるから、普段の行動が極めて悪いD男の場合は
環境順応後の「恋する心」 = 本来の「恋する心」 - ( 悪い印象)ここで「悪い印象」が「良い印象」の反対であることから、( 悪い印象 ) =( -良い印象 )とおくと、
環境順応後の「恋する心」 = 本来の「恋する心」 - ( -良い印象)であるから、
環境順応後の「恋する心」 = 本来の「恋する心」 + ( 良い印象)となる。なんと、「悪い印象」が「良い印象」にすり替わるのである。恐るべし、「環境順応」である。スイカに塩をかけると、ショッパイどころか逆に甘く感じられるのと同じく、ひどいD男がちょっとでも良いことをすると、「ものすごく良いこと」に感じられてしまうのである。前回、
「恋の印象の平均化効果」というものを武器に、「辛(つらい)」が「幸(幸せ)」にすりかわる様子を見てみることにしたい。「辛(つらい)」が「幸(幸せ)」は紙一重なのだ。「辛(つらい)」は「幸(幸せ)」で、「幸(幸せ)」は「辛(つらい)」なのである。と書いたが、これがそうだ。普段の「辛(つらい)」を引くと、マイナスをマイナスすることでプラスに変わり、「辛(つらい)」が「幸(幸せ)」にすりかわるのである。
そして、普段悪いことをしないC男の場合はこれとまったく逆に、普段の良い印象を引いてしまうが故に、環境順応後の「恋する心」には「悪い印象」が加わってしまうのである。「普段良い男」が少しでも悪いことをすると、散々に悪く言われてしまうのと同じである。
さて、こういった環境順応した状態での、A子のC男に対する「恋する心」とD男に対する「恋する心」を眺めてみることにしよう。次のグラフは黒字がA子のC男に対する「恋する心」を示し、緑字がA子のD男に対する「恋する心」を示している。
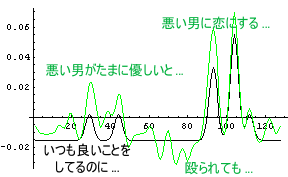 |
なんと、A子は普段悪いD男の方に強い「恋する心」を感じてしまうのである。「おいおい、それでいいのか?」、と言いたくなるような状況である。「オマエはマゾか!?」と、つい言ってしまいそうである。
まぁ、じっくり物を考えないA子はおておいて、それではB子はどうだろうか?きっと、C男と上手くいくだろうB子はどうだろうか?もちろん、「人の良い」C男を選んでくれるだろう。というわけで、次のグラフが、A子とB子のD男に対する「恋する心」を比較したものである。緑字がA子のD男に対する「恋する心」を示し、黒字がB子のそれを示している。
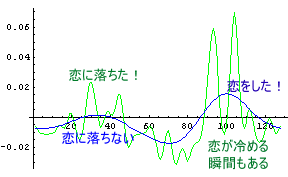 |
何ということだろう。こともあろうに、B子もD男に恋をしてしまうのだ。哀しいかな、C男は失恋してしまうのである。しかも、こtもあろうにD男にである。なんということだ!もちろん、D男がB子にひどいことをした時、すなわち「B子のD男に対する恋する心」が低下した時にA子とD男が別れるという可能性もある。しかし、残念ながらB子は「ゆっくり」タイプなのである。A子と違って、「すごく恋が冷める瞬間」がないのである。A子の場合はとっさのいきおいでD男と別れるという可能性もあるが、B子の場合はむしろD男にひっかかりやすいと言えるかもしれない。
このようにして、「普段は悪い男がたまに優しいことをすると、女の人はふと恋に落ちてしまう」という恐怖のストーリーがいたるところで発生するのである。
私の楽しみ「ちゃろん日記」の2000/03/09の「わしはダメだった」に、「印象の平均化定理」に関するしみじみとした一節があるので、そのまま引用してみたい。
「下僕(仮名)は、不幸な女がどぅやってできるか知っとるか?」「一般相対性理論」によれば、完全なる時空間の基準がない。それと全く同じように、絶対的な幸せの基準など存在しない。本人がそれでいいと言うなら、それでいいのかもしれない。強引を承知で言うならば、それが「恋の相対性理論」である。恋の座標軸は本人が決めるしかないのである。「・・・う?ん」「不幸な女は、フダンはとんでもない男がたま?にほんのすこしだけ見せる優しさが忘れられないコトにより生産される」「・・・・・・」「母ちゃんがそぅだった、こりからもそりは生産されるだろうしそんな女が絶えるコトはないだろう、でもそりでいいのカモ知れんの、本人がそりで幸せだったのなら」
さて、これまで、「できるかな?では何度も「恋のかたち」を何とか目に見える形にしようとしてきた。きっと、それはこれからも変わらないだろう。とりあえず今回の話は、私の好きな本橋馨子の「兼次おじ様シリーズ」の中のセリフを引用して、締めくくることにしたい。
「なぁ兼次、愛はどんな形をしているか知っているか?」
「見た事ないからわかりません。」
「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...」
「もし愛に優劣を決めるものがあればなんだろう?... たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」