1998-11-13[n年前へ]
■明るさを測ろう。 
新技術の女神
今日は浜松ホトニクス(http://www.hpk.co.jp/hpkj.htm)が主催している浜松 PHOTN FAIR 98を見に行った。入場する際に、全員に粗品として、照度計を配っていた。もちろん、私ももらった。 というわけで、今回はいろいろな場所の明るさを測りたい。というわけで、帰る途中、照度計を片手に測り続けてみた。周りから見ると「変なおじさん」に見えたかもしれない。
| 日が照っている時の新幹線ホーム(日陰部) 位置は胸の高さで測定 | 3500 | 雑誌、文庫本を読んでいる人が多い。 |
| 日が陰った時の新幹線ホーム(日陰部) 位置は胸の高さで測定 | 2000 | 明るい景色が目に入らないので、目が痛くなるということがない。 |
| 新幹線の太陽と反対の窓側(12:30) 位置はPCの液晶の上で測定 | 4500 | 明るく、PCのTFT液晶も見づらい。 |
| トンネルに入った時の新幹線の窓側 位置はPCの液晶の上で測定 | 200 | PCの液晶が見やすく、目も疲れない。 |
| 新幹線の太陽と同じ側の窓側(12:45) 位置はPCの液晶の上で測定 | 4500 | 日が直接当っている所が目に入り、目が疲れる。 |
| 居間の理想照度 | 50-100 | これは結構暗い。日本人の居間は普通こんなに暗くないだろう。 |
| 便所の理想照度 | 50-100 | 一体、どのような基準で決めたのだろう? |
| 廊下の理想照度 | 100-200 | |
| 実験室の理想照度 | 200-750 |
理想照度の例によれば、製図作業の場合で750-2500 lxということだから、「日が陰った時の新幹線ホーム(日陰部)」で本を読んでいるのは、なかなか理想的と言えるだろう。ただし、勉強机の理想照度は500-1000lxとなっている。この勉強机と製図作業の差がどこから来るのだろう?
また、「教室、実験室」の理想照度が200-700であるから、PCで作業をするにはトンネルに入った時位でないと辛い。バッテリー駆動で液晶が暗くなっているなら、なお更である。同じ窓側で、太陽と同じ側と反対側でPCの液晶位置での照度自体は同じだったのは少し意外である。ただし、その位置で同じであっても、直接日に当っている所が視野に入るか、入らないかが大きく違う。そのため、目の疲れ方が違うことになる。それは、新幹線ホームの例でも同じである。
上の表の下部にいくつかの環境下における理想照度を示した。ぜひ、測って自分の快適度と重ね合わせて実感してみたい。ちなみに、私の居室は400 lxであるから、なかなか良い感じである。
ところで、「浜松ホトニクスを創業したグループが高柳健次郎に師事した人達であった」というのを初めて知った。高柳健次郎というのはTVを発明した日本人である。前に、NHKの朝の連続TV小説で題材となっていたから、知っている人も多いだろう。そのTVドラマ自体もとても面白かった。もちろん、同じような業界なので、浜松ホトニクスと高柳健次郎の間にどこかで接点はあっただろうと思っていたが、浜松ホトニクスがここまで高柳健次郎に影響を受けているというのが新鮮であった。浜松PHOTOND FAIRでも浜松ホトニクスの歴史を展示するブースで高柳健次郎の作ったTVと同じようなものを展示、実演していた。あの有名な「イ」という文字を表示していた。
そして、高柳健次郎が強く感銘を受けたという言葉が掲げてあった。こういった内容だったと思う。
「新技術の女神は後頭部ハゲだ。新技術の女神を捕まえようとして、後ろから女神を追いかけて後ろ髪を捕まえようとしても無駄だ。女神の正面に先回りし、正面から前髪を捕まえなければ、捕まえることはできない。」
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
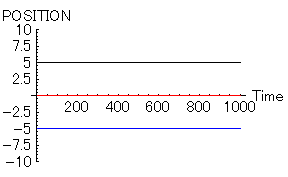 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
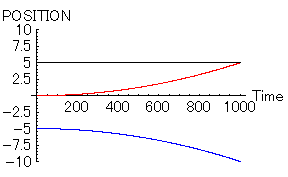 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
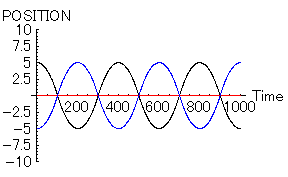 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
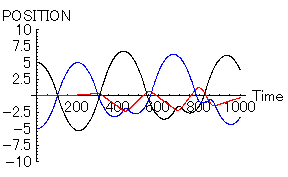 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)
2000-04-02[n年前へ]
■恋の力学 恋のグラフ配置編 
「明暗」の収束を見てみよう
前回、
で漱石の「明暗」における登場人物- 津田
- お延
- 清子
- 吉川
前回は、「津田」と他の登場人物の間の相関しか考えなかった。しかし、登場人物達の動きを考えていくならば、相互の相関を考えなければならないだろう。「続 明暗」の例を挙げるまでもなく、「明暗」の登場人物達がどこに収まっていくのか、「明暗」はどう収束していくのか、は非常に興味のあるところである。そこで、ラスト近辺の各登場人物間の相関を調べてみた。
津田 | お延 | 清子 | 吉川 | |
津田 | 1 | |||
お延 | 0.38 | 1 | ||
清子 | 0.61 | 0.42 | 1 | |
吉川 | 0.10 | 0.063 | 0.26 | 1 |
比較的大きな値の数値を青字で示した。有意であるかはともかく、この数値を見ると、話が「津田」、そして、「清子」を中心として動いていることが想像される(数値からだけでも)。
このような相関、言い換えれば関係を登場人物達が持っているときに、この後人物達の関係はどこに収まっていくのだろうか?この相関値を「互いの関係度」と考え、その値に比例して惹かれ合うと考えたときに、登場人物達はどう動いていくのだろうか?そういったことを調べたならば、そこに示される結果は書かれることのなかった「明暗」の収束する先が示されているかもしれない。
そこで、登場人物達を適当に配置して、登場人物間に働く力を考慮して、登場人物を動かした際に、結果として登場人物達がどこへ動いていくかを調べてみることにした。使うのは、もちろん"Sun"のJavaappletのプログラム例のグラフアプレットである。複数のものがあり、それぞれの関係が示された場合に、どのような配置になっていくかを調べる「グラフ配置問題」を解いてみるのである。今回の問題では、「恋のグラフ配置問題」を解くといっても良いだろう。
もう、いきなりであるが、登場人物
- 津田 = Tsuda
- お延 = Oen
- 清子 = Kiyoko
- 吉川 = Yoshikawa
 |
どうだろうか?「津田」を中心として、登場人物が蠢いているのがわかるだろう。適当に登場人物の位置をマウスで移動させてみると面白い。そして、互いの"Stress"を示してみると面白いと思う。
また、「明暗」の登場人物達の運命を、自分のマウスでコントロールしてみるとどんな感じだろう?それとも、どんな位置に登場人物を持っていっても、結局収まる位置は変わらなかったりするだろうか? だとしたら、それがやはり本来の登場人物の収まる位置かもしれない。
いつか、登場人物間全てを配置して、「明暗」における「人間関係のグラフ配置問題」でも考えてみたいものだ。「恋の力学シリーズ」は奥が深い、とつくづく思うのである。
2000-05-17[n年前へ]
■恋の形を見た人は 
恋の相対性理論
さて、前回
では、三人の登場人物A子 : 「瞬間」的に燃え上がるタイプの女の人達の間で繰りひろげられる色々な「出来事・きっかけ」と、それにより発生する「恋する心」を「恋のインパルス応答」を用いて計算してみた。その結果、C男とB子がカップルになれば「ほのぼの」とした幸せな生活をしそうだ、というところまで考察した。
B子 : 「ゆっくり」燃えるタイプの女の人
C男 : いつも、とっても良い男
今回は、その三人に加えて
- D男 : ほとんどの場合、悪い男
さて、今回登場する「D男 = ほとんどの場合、悪い男」はかなり酷い男である。D男がA子とB子に対して何をしたか時系列を追ってみてみることにしよう。
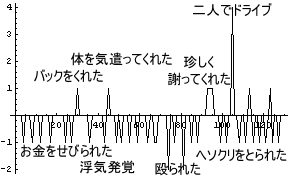 |
- お金をせびり、
- 浮気をするし、
- それを追求すると殴る蹴るの暴行を働き、
- せっせと貯めたヘソクリを奪いパチンコに行ってしまう、
それに対して、前回のC男は次のグラフのように悪いことは何一つしない良い男だ。
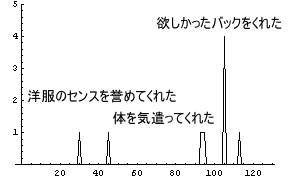 |
悪いことは何一つしない。良いことばかりをしてくれるのである。何とも良い人である。普通に考えれば、女の人の「ハート」はC男ががっちり掴み、D男は警察官にでもがっちり掴まれているのが当然であろう。掴まれたが最後、シャバには二度と出てきてこないで欲しい位である。しかし、そう単純な話ではないのだ。
人の感覚には「順応」というものがある。簡単に言えば「慣れ」である。ひどいことしかしない男と普段接していると、それが当たり前に思えてしまうのである。相対化してしまうのだ。普段のD男に対する印象が「当たり前」に思えてしまうのである。
さて、その「恋する心」の「順応」を計算するにはどうしたら良いだろうか?そう、普段の印象を基準にすれば良いのだ。普段の印象、すなわち「印象の平均値」を「恋する心」から引けば良いのである。例えば、A子のC男に対する「恋する心」を計算してみることにする。次のグラフで黒字が「色々な出来事」と「恋のインパルス応答」の畳み込みであり、本来のあるべき「恋する心」である。そして、緑字が環境順応後、すなわち、本来のあるべき「恋する心」から「印象の平均値」を引いた「恋する心」である。
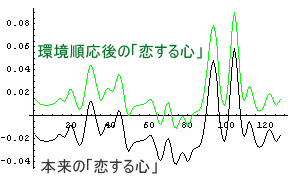 |
この図で、環境順応後の「恋する心」が本来の「恋する心」よりいい印象であることがわかると思う。何故かというと、環境に順応するということは普段の印象が当たり前の状態と思ってしまうことである。普段「悪い」男を相手にする場合は、「悪い」のが当たり前だと思ってしまうのである。数学的には、「悪い」のを引くのであるから、「マイナスを引くとプラスになる」のと同じである。それを式で表してみると、
環境順応後の「恋する心」 = 本来の「恋する心」 - 普段の態度
なのであるから、普段の行動が極めて悪いD男の場合は
環境順応後の「恋する心」 = 本来の「恋する心」 - ( 悪い印象)ここで「悪い印象」が「良い印象」の反対であることから、( 悪い印象 ) =( -良い印象 )とおくと、
環境順応後の「恋する心」 = 本来の「恋する心」 - ( -良い印象)であるから、
環境順応後の「恋する心」 = 本来の「恋する心」 + ( 良い印象)となる。なんと、「悪い印象」が「良い印象」にすり替わるのである。恐るべし、「環境順応」である。スイカに塩をかけると、ショッパイどころか逆に甘く感じられるのと同じく、ひどいD男がちょっとでも良いことをすると、「ものすごく良いこと」に感じられてしまうのである。前回、
「恋の印象の平均化効果」というものを武器に、「辛(つらい)」が「幸(幸せ)」にすりかわる様子を見てみることにしたい。「辛(つらい)」が「幸(幸せ)」は紙一重なのだ。「辛(つらい)」は「幸(幸せ)」で、「幸(幸せ)」は「辛(つらい)」なのである。と書いたが、これがそうだ。普段の「辛(つらい)」を引くと、マイナスをマイナスすることでプラスに変わり、「辛(つらい)」が「幸(幸せ)」にすりかわるのである。
そして、普段悪いことをしないC男の場合はこれとまったく逆に、普段の良い印象を引いてしまうが故に、環境順応後の「恋する心」には「悪い印象」が加わってしまうのである。「普段良い男」が少しでも悪いことをすると、散々に悪く言われてしまうのと同じである。
さて、こういった環境順応した状態での、A子のC男に対する「恋する心」とD男に対する「恋する心」を眺めてみることにしよう。次のグラフは黒字がA子のC男に対する「恋する心」を示し、緑字がA子のD男に対する「恋する心」を示している。
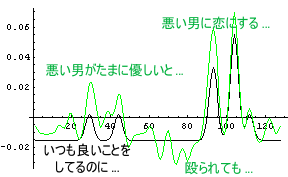 |
なんと、A子は普段悪いD男の方に強い「恋する心」を感じてしまうのである。「おいおい、それでいいのか?」、と言いたくなるような状況である。「オマエはマゾか!?」と、つい言ってしまいそうである。
まぁ、じっくり物を考えないA子はおておいて、それではB子はどうだろうか?きっと、C男と上手くいくだろうB子はどうだろうか?もちろん、「人の良い」C男を選んでくれるだろう。というわけで、次のグラフが、A子とB子のD男に対する「恋する心」を比較したものである。緑字がA子のD男に対する「恋する心」を示し、黒字がB子のそれを示している。
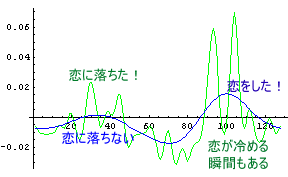 |
何ということだろう。こともあろうに、B子もD男に恋をしてしまうのだ。哀しいかな、C男は失恋してしまうのである。しかも、こtもあろうにD男にである。なんということだ!もちろん、D男がB子にひどいことをした時、すなわち「B子のD男に対する恋する心」が低下した時にA子とD男が別れるという可能性もある。しかし、残念ながらB子は「ゆっくり」タイプなのである。A子と違って、「すごく恋が冷める瞬間」がないのである。A子の場合はとっさのいきおいでD男と別れるという可能性もあるが、B子の場合はむしろD男にひっかかりやすいと言えるかもしれない。
このようにして、「普段は悪い男がたまに優しいことをすると、女の人はふと恋に落ちてしまう」という恐怖のストーリーがいたるところで発生するのである。
私の楽しみ「ちゃろん日記」の2000/03/09の「わしはダメだった」に、「印象の平均化定理」に関するしみじみとした一節があるので、そのまま引用してみたい。
「下僕(仮名)は、不幸な女がどぅやってできるか知っとるか?」「一般相対性理論」によれば、完全なる時空間の基準がない。それと全く同じように、絶対的な幸せの基準など存在しない。本人がそれでいいと言うなら、それでいいのかもしれない。強引を承知で言うならば、それが「恋の相対性理論」である。恋の座標軸は本人が決めるしかないのである。「・・・う?ん」「不幸な女は、フダンはとんでもない男がたま?にほんのすこしだけ見せる優しさが忘れられないコトにより生産される」「・・・・・・」「母ちゃんがそぅだった、こりからもそりは生産されるだろうしそんな女が絶えるコトはないだろう、でもそりでいいのカモ知れんの、本人がそりで幸せだったのなら」
さて、これまで、「できるかな?では何度も「恋のかたち」を何とか目に見える形にしようとしてきた。きっと、それはこれからも変わらないだろう。とりあえず今回の話は、私の好きな本橋馨子の「兼次おじ様シリーズ」の中のセリフを引用して、締めくくることにしたい。
「なぁ兼次、愛はどんな形をしているか知っているか?」
「見た事ないからわかりません。」
「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...」
「もし愛に優劣を決めるものがあればなんだろう?... たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2000-06-16[n年前へ]
■ヘルメットの色空間分布 
学生運動の色空間とグラフ配置
さて、私は「迷信の押し付け」は大嫌いである。もちろん、その人の中で信じている分には結構で、それも文化の一つだとは思う。しかし、それを私にまで押し付けられるととたんにムッとしてしまう。そんな私ではあるが、「占い」はそう嫌いでもなかったりするのが面白いところだ。いや、むろん「占い」を信じているわけでは毛頭無くて、「遊び」として好きなのである。
何しろ、占いというのは「根拠無し」に「決めつける」ことが出来る素晴らしいものである。何の前振りもなしに
「君はお菓子の食べすぎでデブになる。」と言うと、普通であれば張り倒されることだろう。しかし、それを
「君の前世は象だった。だから、君は太る運命だ。」と言えば、どうなるだろうか。悪いのは「前世」や「運命」であって、「口の悪い私」ではないのである。それどころか、
「えぇ〜、なになにその占い〜。教えて、教えて〜」という好意的な反応すら予想される(あくまで予想だけ)のである。これを便利と言わずして、何と言おう。
しかも、占いの特徴の一つは後付けの結論・理由付けが可能、というところにある。その結果、「占い」というものは現実にとても近くなり、さらに「本当らしさ」がアップする。そういうわけで、私は大好きなのである。
例えば、私の職場の私の机の端には、名前、生年月日、アンケート式etc.といったありとあらゆるタイプの占いを職場の人がやった結果がファイルされている。そして、恐ろしいことにそれらの紙には、それを読んだ人の書き込みがあるのである。例えば、私の性格占いの結果をプリントアウトした紙を見てみると、「もう少しイイ子になる必要があります。」という文章の下に赤線が引っ張ってある。この赤線を書き込んだのは誰だか知らないが、実に失礼な輩である。また、「思ったことをすぐ口に出す傾向があります。」という部分は二重線が引っ張られており、これなども世の中には訳のわからないことをする人間がいる良い一例である。そのくせ、「とても心優しいひとです。」という部分は赤線で消されたりしているのが、私としては理解に苦しむ部分でもある。きっと、この書き込みをした輩は「心優しい」という意味を知らないのであろう。
そういうわけで、こういった人々による書き込み・添削のされた占いの結果、すなわち、後付けの結論・理由付けのされた占いの結果と言うのは実に恐るべき迫真性を持つのである。そして、同時に笑うことができる(本人は別にして)、という素晴らしいものなのである。
ところで、私は「色」が大好きである。もう、何回も「色」に関する話題をしているのだから、そんなことは言うまでもないかもしれない。そこで、「色」と「占い」との関連で言うと、一時期「色占い」というものが流行っていた。「XX色で連想する人は誰?」という質問をして、この色で連想された人はあなたにとって恋人、とか、この色は友達、とか占うのである。
私もこの「色占い」が流行ったときにやった記憶があるのだが、これが全く役に立たなかった。役に立たなかった理由の一つに
- 私の周りの人は服なんて着替えない。
- だから、いつも同じ服を着ている。
- その服のイメージ = その人のイメージになる。
そのために、当時の学生の典型的?な姿を下に示してみる。いや、正確に言えば典型的ではなくて、単に目立っていた学生と言うほうが正しいかもしれないが、その姿を示してみたい。
 |
この絵を見るとわかるように、頭の部分を覆うヘルメットというのは何より目立つのである。この人達が身に付けている服装というものは、そんなにカラフルなものではない。いや、ハッキリ言えば、特徴のない色ばかりである。そりゃそうだ、個性的で目立つ色の服なんか着ていたら、個人的に目をつけられてしまう。
しかし、それに対してヘルメットの部分は実にカラフルである。セクトごとに個性ある色分けがされている。人目見ればわかるような色使いがされている。それは、チームスポーツのユニフォームと同じである。敵か味方か一目で見分けがつかないと、困ってしまうわけである。
そして、そのヘルメットの色の印象が強いがために、
その人達の印象 = その色というような状況すら生まれるのである。だから、先の「色占い」のような質問はそのような場においては、何の意味も持たないのである。それは単なるセクト分け問題と化してしまうのである。とたんに、生臭い問題になってしまうのだ。
ところで、さまざまな場所に位置する各セクトが、どのような「色」の住み分けをしているかは、非常に気になるところである。「色」に常日頃こだわってきた「できるかな?」であるから、各セクトのヘルメットの色空間における空間分布を見てみることにしたい、と思う。
そこで、マルチメディア共産趣味者連合 中央委員会の
- ヘルメットで見るセクト( http://marukyo.cosm.co.jp/MET/index.html )
 |
こうしてみると、ヘルメットによる色表現を考えてみると結構広い「色空間分布」になっているようである。カラー画像をヘルメット画像に色分解する、ヘルメットディザなんていうのも実現できるかもしれない。
しかし、これだけではつまらないので、
- 学生活動家組織の変遷 (http://marukyo.cosm.co.jp/KEIZU/gakusei-keizu.html )
そして、グラフ配置の結果の一例を色空間に重ねてみたものを次に示す。
 |
この画像と先程の「ヘルメットの色空間分布」を比較してもらうと、結構似ているのが面白いところだと思う。もちろん、似たような配置になったものを使用したわけではあるが、それにしても面白いと思うのだが、どうだろうか?
私が大学に入学した当時は、セクト間の陣地争いが盛んだった。といっても、私のいた学校がガラパゴス諸島のように(その手の部分では)化石的な学校だったからで、決して古い昔の話ではない。授業をやっている横の廊下で、内ゲバで殺される人がいたり、朝のキャンパスで血みどろの戦いが行われていたりした。実際のところ、それは私にとって結構衝撃的な出来事だった。少なくとも、そのせいで、あの手の陣地争いを大嫌いになったことは確かだ。とりあえず、現実空間ではともかくこの色空間においては、そんな陣地争いがないのが良いところだ。
さて、今回はタイトルをゲバ字(トロ字)っぽくしてみた。ゲバ字(トロ字)というのは、チラシや立て看などでよく使われた(る?)文字のことである。だから、別に「こういう形」というものがあるわけではない。とりあえず、それっぽくしてみたわけであるが、どうも本WEBにはこういうフォントは似合わないようである。うーむ、失敗である。