2011-03-28[n年前へ]
■「ビルの階数」と「エレベータが停まる回数」で「乗り込んだ人たちが”およそ”何人連れ」なのかがわかるの法則 
「ビルの階数」と「エレベータに並ぶ人数」でエレベータが停まる回数がわかるの法則 で登場したのが、こんな法則です。
M階のビル（の一階）で、エレベータの前にN人が並んでいるならば（そのN人がエレベータに乗り込むならば）、平均的に、エレベータが停まる「階の数」は
M ( 1- ( (M-1)/M )^N )
と表されます。
たとえば、お昼間近のデパートやオフィスビルのエレベータに実際に乗り込んで、「エレベータに乗り込んだ人数」と「エレベータが止まる階の数」を眺め・調査してみると、この法則よりも「エレベータが停まる階の数」はかなり少ないことに気づきます。それは、エレベータに乗り込んでいる人たちの中には「一緒に行動する”グループ”」がいるからです。たとえば、エレベータの中に１０人いたとしても、それが５人家族×２組だったとしたら、この法則の「人数」Nには10でなく2を入れ込んでやらなければならないからです。
…ということは、ビルの階数」と「エレベータに並ぶ人数」でエレベータが停まる回数がわかるの法則 は、「ビルの階数(M)」と「エレベータが停まる回数(F)」で「乗り込んだ人たちが”およそ”何人連れ(N)」なのかがわかるの法則、と見ることもできます。
つまり、M階建てのビルの一階でエレベータに乗り込んだら、素早く人数(N人)を数えた上で、（エレベータが止まることを示す）点灯したボタンの数（F)を眺めれば、
G=N / (log(F/M) / log( 1- ( (M-1)/M )))という式を使うことで「フムフム、この人たちは”およそ”G人連れなんだろうな」などと推理すれば良い、というわけです。
エレベータという密室中に乗り込んだ人たちが、連れ同士が言葉を一言も交わすことがなかったとしても、こんな「法則」のごとく統計・数学的な推理をすることができます。日常生活の中には、こんなミステリーが満ちあふれていて、開花を待つ桜の蕾（つぼみ）のように、解き明かされる瞬間を待ちわびているような気がします。
2011-08-15[n年前へ]
■実は体育会系な 「京都市鴨川源流」を廻る「理系風デート」
今はカリーニングラードと呼ばれ、かつてはケーニヒスベルクという名前だったバルト海沿いにあるロシアの街を舞台にして、「流れる川により区切られた土地を、一筆書き状にすべて渡り、スタート地点に戻ってくることができるか？」という「謎かけ」が、「ケーニヒスベルクの橋渡りの問題」です。
ケーニヒスベルクでなくとも、日常生活をする中で眺める街の景色の中にも、「ケーニヒスベルクの橋渡りの問題」は結構顔を出しているものです。たとえば、それは川崎の東京湾寄りのTOKIOのDASH海岸がある辺りに行けば、「ケーニヒスベルクの橋渡り問題」な案内看板を見かけることができます（街で見かけた「ケーニヒスベルクの橋渡り問題」）。そして、京都市街東部を流れる鴨川辺りにも、そんな「ケーニヒスベルクの橋渡り問題」があって、そこを巡る「理系風デート」が有名？であったりします（「京都市鴨川源流」を廻る「理系風デート」）。
実際に鴨川辺りに行くと、「この橋渡り問題を解くべし」と、まさに「ケーニヒスベルクの橋渡り問題」な地図・看板がたくさん掲げられています。面白いことに、それぞれの地図ごとに川に渡された橋の数が異なっていて、つまり、地図ごとに「答え」が違うことに気づかされます。ある地図では、一筆書きが可能だけれども、ある地図では一筆書きをすることは不可能だということがわかったりするのです。…それを逆に言えば、地図ごとに答が違うからこそ、「ケーニヒスベルクの橋渡り問題」な地図を見つけるたびに、新しい問題（地図）を解く楽しみが生まれる、ということなのです。
「一筆書きできる地図」を見つけ出し、一筆書きをしつつ川縁（かわべり）を回ってみても楽しいし、あるいは、川端（かわばた）にあるたくさんの「ケーニヒスベルクの橋渡り問題」な地図を眺め、それら「ケーニヒスベルクの橋渡り問題集」を解いて回るのも面白いものです。
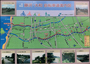
ところで、実際に「京都市鴨川源流」を廻る「理系風デート」をしてみると、結構長い距離を回らなければいけないことに気づきます。徒歩で歩き回るのはもちろん大変ですし、自転車で走り回るにしても、…やはり結構な時間ペダルを漕がなければなりません。また京都市街は南に比べて北の方が標高が高い、当たり前ですが、鴨川下流よりは上流の方が標高が高いわけですから、（目に見えないほどの斜度とはいえ）北上する時には坂を登る体力が必要です。
たとえば上に貼り付けた地図のように、橋と橋の間の距離や、橋と橋の間の標高差が書かれている「ケーニヒスベルクの橋渡り問題」も見かけます。こんな問題（地図）を見かけたならば、「一筆書きをすることができるか」という問題だけでなく、「移動に必要な体力を最小化するにはどうしたら良いか」という（いわゆる）制約条件付き最小化問題を解いてみるのも興味深いかもしれません。…そして、その最小化問題を解いたなら、地図から解き明かした答えを確かめるべく、ひたすら鴨川の川縁（かわべり）を汗をかきつつ走り回るのです。
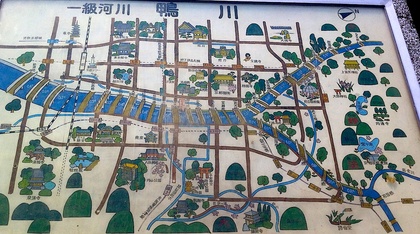
「京都市鴨川源流」を廻る「理系風デート」は、実はとても体力を使う、実はかなり体育会系なデートです。少しだけ頭を使って考えたことを、体力と根性で確かめる、そんな楽しい「ケーニヒスベルクの橋渡り問題」なのです。
2011-10-03[n年前へ]
■「機械的な能力だけを持つものからは有効な助力は得られない」
岡部恒治「考える力をつける数学の本
（今まで）単なる機械的計算能力を有するものから、有効なる助力を得たろうと思われる場合はない。
カール・フリードリヒ・ガウス（高木貞治『近世数学史談』）
2012-04-17[n年前へ]
■百次方程式の係数を複素平面上で動かして、百個の解のダンスを眺め・楽しんでみよう!?
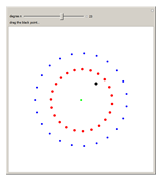多項式からなる代数方程式の「係数」をマウスでつかんで動かした時に、「（その代数方程式の）”解たち”の配置」と「”解たち”が動き回るようす」を眺めたいな…と思ったのですが、ググってみると「x^n + b x + 1 = 0 おいう代数方程式の係数bを複素平面上で動かした時に”解たち”がどのような配置になるか・どのように動き回るか」をインタラクティブに味わえる・楽しむことができる（Monodromy of z^n + b z + 1 = 0）というものがありました。
そこで、”x^n + b x + 1 = 0”という二次から百次までの代数方程式で、係数”ｂ”を複素平面上で（マウスで）動かして（青丸）、（その動きに応じて）解の集団（赤丸）が形作る美しいダンスを眺め・楽しんでみました。
中学生くらいの頃、"X^2+2=0"といった方程式を（各々の軸が実数の）XY平面上で黒板の上で眺めつつ、その黒板上に描かれたXY平面には、"Y＝X^2+2"というグラフと"Y=0"というグラフが「どこでも交わっていない」ようにしか見えないのに、方程式の「答え」は「（どこかに）２つの解がある」というもので…それは理不尽で不思議で…つまりは納得できなかったような気がします。
あの頃、複素平面上に複素数値を描いたグラフを見ていたら、黒板の上で多項式の解が複素平面上で円を描いてフォーク・ダンスを踊る風景を眺めていたら…数学に恋をしていたかもしれない、と思います。
オクラホマ・ミクサーやマイムマイム…黒板の上の複素平面上で代数方程式の係数が動くにつれ、その方程式の解の群団が踊るフォークダンス…が今日見た景色、です。
2012-06-21[n年前へ]
■「ケーニヒスベルクの橋渡り問題」 藤沢・江の島"境川サイクリングロード" 編
天才オイラーが解き明かした「バルト海沿いにあるロシアの街ケーニヒスベルクで、街を流れる川に架かる7つの橋を、一筆書き状にすべて渡り、（どこでも良いから）スタート地点に戻ってくることができるか？」という”ケーニヒスベルクの橋渡りの問題”」は、私たちが日々過ごす街にも溢れています。
たとえば、神奈川県は川崎・鶴見の辺りにある『街で見かけた「ケーニヒスベルクの橋渡り問題」』や、あるいは京都の町で「鴨川源流で眺める理系風デート」…といったように、どんな町にも一筆書き問題は潜んでいるのです。
今日は、東京都町田市近くから神奈川の江の島に流れる「境川」に掲げられていた「ケーニヒスベルクの橋渡り問題」を眺め・挑戦してきました。これまでに挑戦した「橋渡り問題」の中では、最も橋が多く・距離も長い…巨大な「一筆書き・橋渡り問題」です。
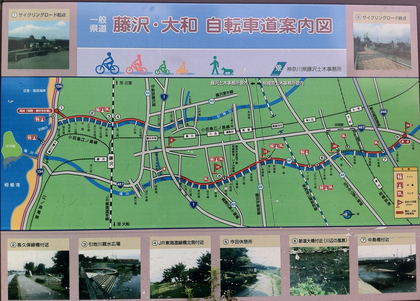
ところで、境川の「ケーニヒスベルクの橋渡り問題」は、江の島を領域に入れてしまうと、「一筆書きできないことは自明」です。何しろ、地図上は橋がひとつしか無いので、江の島は「その場所をスタート地点としたら、戻って来ることができない、けれど、通過することもできない場所」であることが明らかだからです（本当は、江の島には橋が２本かかっているのですけどね）。
…かつてケーニヒスベルクと呼ばれたバルト海沿いのカリーニングラードという街に、「江の島」のような島があったとしたら、オイラーのような天才でなくとも、容易に「ケーニヒスベルクの橋渡り問題」を解き明かすことができたのかもしれない、一筆書き問題が成立するための条件をいともたやすく気づいたのかもしれない、と想像したりします。
これが、今日眺めた「理系の散歩道」です。
」など。