2000-02-27[n年前へ]
■「文学論」と光学系 
漱石の面白さ
前回、
でさて、モナリザと言うと、夏目漱石と「モナリサ」にも言及しなければならないだろう。と書いた。何しろ
- 恋の力学 三角関係編 - 恋の三体問題 - (1999.12.27)
- 草迷宮・空間'99 - ネコの目から見た世界- (1999.11.05)
- 「こころ」の中の「どうして?」-漱石の中の謎とその終焉 - (1999.09.10)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- [Scraps]人静月同照 - ぼくらが旅に出る理由- (1999.06.17)
その漱石は「永日小品(リンク先は青空文庫)」(リンク先は青空文庫)の「モナリサ」中で
「モナリサの唇には女性(にょしょう)の謎(なぞ)がある。原始以降この謎を描き得たものはダ・ヴィンチだけである。この謎を解き得たものは一人もない。」と書いている。女性には興味がなかったとも言われ、ずっと付き添っていた男性との関係も噂されるダ・ヴィンチである。ここらへんは、果たしてどうか?とも思う。むしろ、新宿のホストクラブのホストの方が女性(にょしょう)の謎(なぞ)については詳しいのではないかとも私は考えたりもする。
が、そんなことはどうでも良い。漱石はレオナルド・ダ・ビンチのモナリザに興味を持ち、小品を書き上げたのである。そこで、漱石とダ・ヴィンチの相似点を考えてみたい。
レオナルド・ダ・ビンチの著作には「文学論」というものがある。漱石にも同じ名前の「文学論」がある。この「文学論」はこれまで読んだことがなかったのだが、
- 「漱石の美術愛」推理ノート 新関公子 平凡社 ISBN4-582-82927-9
- 遠近法
- 漱石の文学論の「公式」
これが、とても面白い。仮名遣いが古いため、なかなか目に入ってこないのであるが、とても面白い。これは絶対に文庫本にすべきである。眺めているだけでも面白い。
まずは、冒頭のフレーズがいきなりこうである。
およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。まるで、理系の教科書である。そして、目次(編)を大雑把にさらってみる。
- 文学的内容の分類
- 文学的内容の数量的変化
- 文学的内容の特質
- 文学的内容の相互関係
- 集合的F
また、「文学論」中では、例えば、浪漫派と写実派の違いについて数値的な比較を通じて述べられていたりする。実に「科学的」な思考による「文学論」である。いや本当に漱石は凄い。
さて、中の文章を解説する力は私にはない。そこで、中の図表を示してみることにする。そこで適当に思うことなどを書いてみようと思う。
次に示すのは、「文学論」の冒頭の方で「意識の焦点・波形」を説明した図である。
 漱石全集第十一巻より |
この図は人間が何かを感じるときには焦点にピークがある、そして、その周りはぼやけたものが連続的に続いているということを示したものだ。これなど、
の時の「恋のインパルス応答」を彷彿とさせる。あの時の「恋のインパルス応答」を次に示してみる。 |  |
この意識される恋心(f)は先の「意識の波形」と全く同じである。ある出来事(F)と、それに付着する情緒(f)を示したものとなるわけだ。付着する情緒(f)というのは中心が一番大きく、その周りにぼやけたものが繋がっているというわけである。人間の感じ方・情緒を光学系と結びつけているわけだ。
いやはや、「恋のインパルス応答」と同じようなことを考える人はやはりいるものである。まさかそれが漱石だとは思いもしなかった。しかも時代を考えると凄まじい、としか言いようがない。
そして、さらに次に示すのは
およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。ということを示す図である。先の - 「漱石の美術愛」推理ノート - ではこの図と遠近法の関連が述べられている。
 漱石全集第十一巻より |
ここで、縦軸は「時間」となっており、横軸は「色々な出来事」である。ある人が感じた「色々な出来事」を時間方向に収斂させていくと、そこには「作者自身の視点がある」というわけだ。これが漱石の言う「文学論」の中心である。
この図などカメラや望遠鏡の光学系を彷彿とさせる。「光学系の一例」を以下に示す。
 |
先の「文学の焦点」を示した図はレンズで光を焦点に集めるのと全く同じだ。いや、「焦点から光を投光する」のと同じと言った方が良いだろうか。以前、
で、景色に焦点を合わせて、フィルムに結像させるのがカメラだ。しかし、フィルムに写っているのは単なる景色ではない。カメラの光が集まる焦点にフィルムが位置していると思い込むとわからなくなる。逆から考えてみれば簡単に判るはずだ。カメラの視点にフィルムが位置しているのだ。フィルムに景色が写っているのではなく、フィルムが景色を選び、景色を切り取っているのである。と書いたのと全く同じである。その光学系には歪みもあるかもしれないし、色フィルターもかかっているかもしれない。しかし、とにかく焦点にはその人自身がいるのである。写真に写っているのは、撮影者の視点なのである。写真を見れば、撮影者が、どこに立ち、何を見てるかが浮かび上がってくるはずである。フィルムに写っているのは撮影者自身なのだ。
写真でも文章でもとにかく何であっても、色々感じたことを表現していく時、その焦点には表現者自身がいる。私の大好きなこの2000/2/25の日記なんか、実にそれを感じるのである。
2000-06-11[n年前へ]
2000-06-13[n年前へ]
■コンクリートの隙間に 
足元にあるカメラオブスクラ

写真を撮り出した人が必ず罹る病が、「街中のありふれたものに美を感じだす」ことだと思う。カメラを使い出した最初の頃には、誰しも必ず罹るのではないだろうか?街中の看板やちょっとした何かにレンズを向けた人は多いと思う。私などは、いつまで経っても写真初心者だったりするので、今でもその病は治っていない。カメラをたまに持つと、どうしても単なる路肩などにレンズを向けてしまう。私はこんなコンクリートの隙間がとても好きなのだ。
デジカメを持ち歩く今でも、やはり道のアスファルトと建物のコンクリートの隙間や、道端の街路樹との隙間には何故か惹かれてしまう。桜の樹の下から目をそらすことができなかった人がいるように、私はその隙間から目をそらすことができない。それは、文字通りの「隙間」だけでなくて、もっと広い意味でも「隙間」も含めてである。
そんな隙間を意味する"aperture"は、同時に光学系の絞り・有効口径をも意味する。"aperture"が大きければ、焦点が合っているところは明るく映し出される。そして、分解能は高くなり、はっきりと物事が見えるようになる。しかし、それはあくまで部分的な話である。なぜなら、"aperture"が大きければ大きいほど被写界深度は浅くなり、焦点が合うのはごく一部だけになってしまうからだ。その結果、焦点が合っていない個所はボケて、そこに何があるのか見えなくなってしまう。部分的には、はっきりと写し出されていても、それは部分的だ。ある部分を正確に描写しようとすればするほど、他の部分が見えなくなることがある。
カメラオブスクラの光を通す「小さな隙間」のように、その隙間を小さくしていけば、はっきりと世界が写るようになる。隙間を小さくすればするほど、世界ははっきりと、そして暗くなる。そして、"aperture"が限りなく小さくなってしまえば、光が届かずにもう何も見えなくなってしまうだけだ。それでは、もう何も写らなくなってしまう。
そんなわけで、こじつけすぎるかもしれないけれど、ちょっとした大きさの隙間だからこそ、見える色々なものがあるはずだ、と私は思う。中途半端で、あいまいで、長続きしそうにもない隙間のような場所だからこそ、ボンヤリとしてはいても、色々なものが写っているかもしれない、と思ったりする。
2001-06-04[n年前へ]
■あなたの声が、すぐそばにある 
高原の向日葵と月見草 編
昨日、東京駅の地下街にある「王様のアイデア」でこんなものを買った。見ての通り、ピストル型の集音マイク"SonicExplorer"だ。その数日前にその集音マイクを初めて見かけたのだが、遊んでみるとどうにも気に入ってしまって、次に見た時には必ず買おうと決めていたのである。
 |
数日前に、その"Sonic Explorer"を見かけた時は出張帰りだったのだが、地下街の雑踏の中で「頭にヘッドホンを被り、ゴルゴ13のように集音ガンで狙っている」様子はさぞかしアブナイ奴に見えたに違いない。現に、私が雑踏の中に"SonicExplorer"で狙いをつけていたときには、一緒に出張していた仲間が二・三歩後ずさりして、私の側から離れていったくらいである。自分でも怪しい姿だとは思ったのだが、そんなことを忘れてしまうくらいに面白かったのである。こんなおもちゃみたいな外見に似合わないほど、これを使うと遠くの音がピンポイントでよく聞こえるのだ。地下街の雑踏の中で遥か向こうで携帯電話で話をしている人に"SonicExplorer"を向けると、私の耳元でささやいているかのように聞こえてくるのである。もちろん、遥か向こうといってもたかだか20mくらいではあるのだが、雑踏の先の20mというのはずいぶんと先に感じる。しかし、"SonicExplorer"の先のパラボラ面は見事にその遠く先の音を集めてくれる。
ところで、遠く離れた人の声はどうして聞き取れないのだろうか?それはもちろん、遠く離れた人の声は小さくしか聞こえなくなって、その人以外が発する雑音に埋もれてしまうからだろう。それでは、人がしゃべる声は距離が離れるとどの程度小さくなるだろうか?
音波が四方八方に等方に拡がっていくとすれば、音の大きさは音の発信源からの距離の二乗に反比例すると考えるのが自然である。つまり、喋っている人からの距離が10倍になれば、その人の声は1/100の大きさでしか聞こえないことになる。20m先で携帯電話で喋る人の声は、1m隣でささやく人の声のわずか1/400の大きさなのである。それでは、雑踏の中で溢れる他の音に埋もれてしまうのは当り前である。
そんな声を聞き取りたい時にはどうしたら良いだろう?そんな時、私達は耳に手を当てて、耳を澄ませる。掌で音を耳に集めて何とか声を聞き取ろうとするのである。それと同じく、この"SonicExplorer"は、先端のパラボラ面で焦点にあるマイクに音を集めて増幅するのである。それでは、"SonicExplorer"は私達の耳に比べてどの程度音を多く集めているだろうか?
そもそも、私の耳の大きさはどの程度だろう?耳はそんなに効率的に音を集めそうな形状をしているわけではなさそうだから、有効な集音面積としては直径1cmの円といったところだろう。それに対してこの"SonicExplorer"のパラボラは直径20cm程だ。ということは、直径にして20倍、面積にして二乗で400倍の面積で音を集めることができるわけである。音を集める程度は音を集める面積に比例するだろうから、"SonicExplorer"を使えば人間の耳の400倍もの鋭さで音を聞き取ることができるわけだ。400倍ということは、つまりは先ほどの「20m先で携帯電話で喋る人の声」と「1m隣でささやく人の声」との違いと同じというわけで、結局のところ"SonicExplorer"を使えば「20m先で携帯電話で喋る人の声」が「1m隣でささやく人の声」であるかのように聞き取ることができる、ということになる。
ここで面白いのは、音が小さくなってく様子は距離の二乗に比例し、音を集める量は集音面のパラボラの直径の同じく二乗に比例するから、n倍遠くの音を元と同じように聞き取りたかったら、集音面の大きさ(長さ)をn倍にしてやれば良い、という単純な関係にあることである。20m先の声を1m横の声と同じように聞き取りたかったら、耳の大きさ(長さ)を20倍にしてやれば良いのである。
そんなことを考えていると、ふと二十年位前のことを思い出した。その頃、私は夏になるといつも長野県の野辺山あるいは川上村というところに滞在していた。その数年前まで、私はその野辺山で暮らしていたのである。そして、野辺山にある45mミリ波望遠鏡の建設が佳境に入った頃だったのだろうか、その頃私の父は半分野辺山で暮らしていた。下の写真は八ヶ岳の麓にあるその45mミリ波望遠鏡である。
 http://www.icon.pref.nagano.jp/usr/minamimaki/sawayaka.htm |
そんな二十年位前のある日、父がこんなことを言った。
「45mのアンテナを赤岳(八ヶ岳の最高峰)に向けて、副鏡(焦点)の場所にいると赤岳の上にいる登山客達の話す声がまるで自分のすぐ横にいるかのようにガヤガヤと聞こえてくるんだよ」一体、それは本当だろうか?上の写真を見ても、赤岳(八ヶ岳の最高峰)の山頂は野辺山の45m望遠鏡の位置から遥か彼方に見える。少なくとも、その頃の私からすれば遥か先のずっと遠くに見えていた。今でもそれは同じことだろう。やっぱり遠く彼方に見えると思うし、その山頂でワイワイガヤガヤと話す登山客達の声が聞こえるとは思えない。
そこで、試しに地図で野辺山の45m望遠鏡と赤岳の山頂の距離を確かめてみると、直線距離にして10km程である。下の地図で赤い■の位置辺りが野辺山の45m望遠鏡が建っているところだ。10kmということは、メートルにして一万メートルである。メートルに直したところで、やっぱり遠いことには変わりない。
 |
それでは、先ほどの"Sonic Explorer"と同じように考えてみることにしよう。45m望遠鏡のパラボラ面は人間の耳(ここでも直径1cmとしよう)の45m/1cm= 4500cm / 1cm = 4500倍である。ということは、5000m先、すなわち5km先の音が1mのすぐそばにいる人の声と同じように聞こえるということになる。すると何ということだろう、10km先の八ヶ岳の山頂でワイワイガヤガヤと話す登山客達の声は、すぐ2m横でワイワイガヤガヤと話しているかのように聞こえることになる。もちろん、それは理想的な場合の話ではあるが、先の父の話は結局のところ何の不思議もないごく当り前の話だったわけである。
上の写真のような、八ヶ岳の麓にそびえる白い45m望遠鏡ももちろんかっこいいけれど、私が野辺山に住んでいた頃にはまだその45m望遠鏡は建っていなかった。私がいた頃には、下の写真の中に見える朱色の野辺山太陽電波観測所の野辺山干渉計のパラボラアンテナだけが野辺山の高原に点在していた。野辺山干渉計はもう今では現役ではないけれど、今でもやっぱりイースター島のモアイのように大空に向いているはずだ。私は白く輝く45m望遠鏡も大好きだけど、その横に点在している朱色に塗られた鉄骨で支えられている野辺山太陽電波観測所の野辺山干渉計の方が大好きだ。
 http://solar.nro.nao.ac.jp/nori/html/introduction-j.html |
現役を引退した今ではどうなのだか知らないけれど、野辺山太陽電波観測所の野辺山干渉計のパラボラアンテナは太陽電波を捕らえるためのアンテナだったので、いつも太陽の方を向いていた。まるで、巨大な向日葵のように忠実に正確に太陽のある方向にパラボラ面を向けていたのである。だから、太陽が強く照らす晴れた日も、薄暗い雨の日も朱色の鉄塔の上のパラボラアンテナを見れば、太陽の方角はいつも一目瞭然だったのである。
そういえば、私が子供の頃、一時間かけて歩く家から分校までの4キロメートルばかりの道端には、たくさんの月見草が咲いていた。高原の中で高くそびえる赤く巨大な「向日葵」達と、歩く私のすぐ横に咲いている黄色い「月見草」が私はとても大好きだった。
眩しい太陽を追いかける「向日葵」達も、静かに照らす月を見る「月見草」もどこか遠くの声を耳を澄ませて聞いているのだろうかとか、その声をすぐそば近くに感じているのだろうかとか、少し思ってみたりした。
2001-08-07[n年前へ]
■「ボケ」た背景で包み込め 
デジカメ画像をキレイにボカそう アルゴリズム編
最近、新しいデジカメを物色中である。私はこれまではFinePix4700zを使っていたのだけど、そのFinePixが半年程度で壊れてしまった。というわけで、C-4040ZOOMがどんなものか期待しているところである。
壊れたFinePixと言えば、そもそも壊れたFinePixは一台ではなかった。私はすでにFinePixを二台も買っているのだ。そして、もうすでに二台とも壊れてしまっているのである。連続殺人事件ならぬ、連続カメラ自殺事件なのである。
まず、一台目に買ったFinePix700ははメキシコのティファナでポケットから落としたら、バッテリーから電源が供給されなくなった。もちろん、ACアダプターを使えば立派に動くのだけれど、それでは少しばかり機動性に欠けてしまう。まさか発電機を持ち歩くわけにはいかないし、コンセントの近くでしか撮影することができないとなると、それは非常に困ってしまう。そこで、すかさず二代目としてFinePix4700zを私は買った。ところが、買ってから半年位たったある日、今度は勤務先の駐車場でポケットから落としてしまった。すると、今度はファインダー視野がズームに連動しなくなって、なおかつレンズがまるでジョイスティックのようにあらゆる方向に曲がるようになってしまった。
こんな風にデジカメはとっても壊れやすくて、半年毎にデジカメ出費を強いられる私に周囲は「落としたオマエが悪い」と非常に冷たいのである。残念なのだ。「そういうのは壊れたんじゃなくて、壊したんだ」と被害者である私をまるで加害者のように告発する人さえいるのである。連続カメラ自殺事件は実は他殺で、しかも犯人は私だと告発する輩さえいるのだ。ひどい話である。
ところで、C-4040に期待しているのは、コンパクトで、レンズアダプターが使えて、レンズがF1.8と明るいことなのである。コンパクトなのは持ち歩くために必要だし、私はなんと言っても超広角デジカメが欲しいのだが、そんなデジカメはないので、ワイドコンバーターを付けたいのでレンズアダプターが必要なのである。明るいレンズの方は、うす暗い中でも撮影する時に重宝しそうなので、少し期待しているのである。
ところで、この位明るいレンズであれば、もう少しぼかすことができるものだろうか?デジカメで写真を撮ってもどうしてもボケない。35mmフィルムを使っているカメラなどと比べるともう全然ボケない。もうほんとにボケない。
例えば、35mmカメラで135mm F4.5開放のレンズなら、ピントの合ってない背景はこの位はボケる。これは京都の哲学の道近くにある吉田山で撮った写真だ。
 |  |
ピントが合っている位置以外は光がボケて、キレイなボケが発生する。どちらの写真も絞りは開放で撮影しているので、後ろの風景はほぼ丸くボケている。ぼかせばキレイというわけではないけれど、背景などがごちゃごちゃしている中で対象物だけを浮き上がらせたい場合には、「ボケ」させるととても良い感じになる。
しかし、デジカメではそうそう簡単にボケた画像を撮影することはできない。35mmフィルムに比べて、CCDサイズが小さいからである。35mmカメラよりAPSカメラはもっとぼけなくて、それよりデジカメはさらにボケないのである。そんな様子を見るために、二台目として買ったFinePix4700zで「ボケ」を意識して撮影してみたものが下の写真である。手前の植物にピントが合って、奥の道の先はボケてはいるのだけれど、それでも先程の写真などとは比べものにならないほどわずかしかボケていない。
 |
ところで、このような画像の「ボケ」を考えるとき、「ボケ」た画像をシャープに復元しようという話は非常にポピュラーな話題である。例えば、本「できるかな?」でもこれまでに
といった感じで遊んできた。また、さらには「恋の形」を復元しようとしたとか、このようなアプローチを遥か昔に考えていた漱石の「文学論」を振り返ってみたりしたきたのである。しかし、これらはいずれも「ボケたデータを復元する」という問題であった。一方、この逆のアプローチである「シャープなデータをボケたデータにする」という問題も結構ポピュラーである。例えば、音楽をホールやライブハウス風にボケた音にするDSPはかなりの数のオーディオ装置に付けられている。これも、もともとはシャープな音声データが部屋の中でボケていく様子をシミュレートする回路である。また、画像に関する話題でも、ピント位置をずらした複数の画像から任意の「ボケ」画像を作成するといった話題もたまに見かける。
そこで、「できるかな?」でもデジカメ画像を35mmカメラ風にキレイにぼかすことに挑戦してみることにした。今回は、まずはアルゴリズムを確認して、次回以降で簡単プログラムを作成してみることにしたい。
まずは、似たようなソフトウェアがあるかどうか、Googleで適当なキーワードを使って検索をかけてみると、IrisFilter(http://www.reiji.net/iris/)というソフトウェアがあった。これは、「写真のぴんぼけを再現する」というフィルターだった。サンプル写真などを見てみると、これがなかなかきれいだった。例えば、早朝の御殿場の路上を「在りし日のFinePix4700z」で撮影した写真にこのフィルタをかけて、「ボケ」を加えてみたのが下の画像である。
 |  |
ここではこんな![]() 六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
WEBページの記載によれば、このIris Filterは「フィルム特性曲線を利用し、レンズから通った光がフィルムを感光させる様子を再現しています」ということである。なんでも、特許も国内・USP共に出願済みということだが、特願2000-100042もU.S.PTO 09/772532も未だ公開にはなっていないようで、残念ながら特許の内容を読むことはできなない。
このWEBページの記述の中で面白いのは、「データ上の数値をそのまま拡散させる従来のPhotoshopをはじめとした画像処理ソフトと違い、実際のフィルムに当たる光の量(露光量)を逆算し、その露光量をもってピントがずれている様子を再現します」という歌い文句でPhotoshopの「ガウスぼかし」と比較広告してある部分である。
試しに、先の画像をIris Filterで「ボケ」を加えた画像と、Photoshopの「ガウスぼかし」とで「ボケ」を加えた画像を比較してみると、下の二枚の画像のようになる。確かにIrisFilterの売り文句通り、こうして比較してみるとPhotoshopガウスぼかしが写真の「ボケ」っぽくないのに対して、IrisFilterの「ボケ」が写真のそれっぽいことが良くわかる。
 |  |
さて、お仕着せのソフトを使ってみるだけではなくて、自分でデジカメ画像をキレイに「ボケ」させてみることにしたい。というわけで、hirax.net風「ボケ」フィルターの動作を考えてみる。
まずは、毎度のことだがオリジナル画像が「ボケ」る様子を計算する式は
逆フーリエ変換( フーリエ変換( オリジナル画像 ) x フーリエ変換(ボケ具合 ) )と表すことができる。詳しくは、「宇宙人はどこにいる?」の回でも読んでもらうことにして、簡単に言えば周波数領域でオリジナル画像とボケ具合を掛け算をしさえすれば良いのである。つまり、今回のデジカメ画像をぼかす場合だったら、
- デジカメ画像と「ボケ」具合をそれぞれフーリエ変換し周波数空間に変換
- 周波数空間で乗算を行う
- 逆フーリエ変換して実空間に戻す
じゃぁ、早速やってみようとなるわけだが、その前にもう一つ注意することがある。それは、RGB画像の数値というものは実は元々「明るさを対数変換した値」であるということなのである。人間の目も含めて世の中の大抵の材料は対数的な感度を持っている。例えば、人間の目に「2倍明るい」という場合に、光は「2倍明るい」というわけではない。その場合には指数的にX^2倍明るいのである(ここで、xの値はそれぞれのデバイスによって色々と違う)。その明るさをRGB画像の数値データにする時に、明るさの対数をとってLog[x,X^2]で2という数値として表しているわけだ。
RGB画像の数値が「明るさを対数変換した値」だというようすの一例を示すと下の図のようになる。
横軸 = 0〜255の数値データ 縦軸 = エネルギー  | 横軸 = 0〜255の数値データ 縦軸 = エネルギー  |
逆に明るさからRGB画像の数値データへの変換グラフは例えばこんな感じである。RGB数値で200と255と言っても実はその明るさは大違いであることがわかると思う。
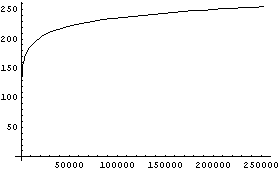 |
だから、この手の処理を行う際には、まずは指数変換してから処理を行い、そしてその後対数変換してやらなければならないわけだ。もちろん、今回のデジカメ画像をぼかす場合にも、RGB画像の数値をまずは指数変換した後、「ボケ」演算を行って、その演算結果を対数変換でRGB画像の数値に戻してやらなければならないのである。といっても、別に難しい話ではなくて画像を扱う装置だとごく当り前の話だ。
そう、「ボケ」演算のhirax.net風レシピはたったこれだけ〜というわけで、早速このレシピに従ってhirax.net風デジカメ「ボケ」フィルターをかけてみたのが下の画像である。キレイな「ボケ」画像ができあがっていることが判ると思う。
 |
ところで、デジカメ画像のRGB画像の数値を指数変換したものに「ボケ」演算を行ったわけだけれど、もしRGB画像の数値そのものに対して「ボケ」演算を行ったら、どんな結果になるだろうか?つまり、「データ上の数値をそのまま拡散させる」やり方をしたら、どうなるのだろうか?そこで、試しにRGB画像の数値そのものに対して「ボケ」演算を行ってみるとこんな結果になる。
 |
何だかボンヤリとにじんだだけの「キレイじゃない」写真になってしまっている。それは、当り前である。本来2倍明るいものはX^2倍明るいわけで、すごく光の量は2倍どころでなく多いわけだ。それが広がる量を仮にRGB数値そのまま2倍として扱ってしまうと、その光の部分は薄暗くなってしまう。コントラストのはっきりしない、ぼんやりとした写真になってしまうわけだ。ちゃんと、X^2倍のデータとして扱ってやらなければならないわけである。
試しに、指数処理したものと線形処理をしたものとを並べてみるとその画像の違いがよくわかるだろう。
キレイなボケ画像(指数処理)  | キレイじゃないボケ画像(線形処理)  |
さて、今回はデジカメ画像の「ボケ」フィルターのhirax.net風レシピを確認してみた。次回(と言ってもいつになるか…)以降に、このレシピに従って実際にソフトを作成していこうと思う。
ところで、「文学論」の中で漱石は「ボケ」は焦点的印象又は観念に付随する情緒を意味する、と言っている。それは、言い換えれば「何かの出来事をきっかけとして感じた怒り・悲しみ・喜びなどの感情がボケである」ということだ。そして、さらに言えば、写真で背景をぼかすということは、つまり「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて包み込む」ということなのである。
だから、何かを撮影する時に対象物の背景をぼかすということは、「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて対象物を包み込んで、そして対象物を浮き上がらせる」ということなのかなぁ、とぼんやりと考えてみたりする。そんな写真は対象物を写しこんでいるのと同時に、それを包みこむ背景も写しこんでいるンだろうなぁ、と考えてみたりする。
