hirax.net::Keywords::「直径」のブログ

■偵察衛星の「視力」はいくつ!?　

30倍の双眼鏡で覗くアフリカ人

　ほんの何週間か前、米軍がイラクへ侵攻し始めた頃、テレビのワイドショーでは米軍の偵察能力の話題がよく取り上げられていた。なんでも、10cm前後の分解能があって飛行場に止まっている車の車種まで判別することができるとか、歩いている人を認識できるとか、そりゃまたビックリの偵察衛星の性能を事細かに報じていた。
 そしてまた同じ頃、北朝鮮の軍事施設の監視などを目的として打ち上げられた日本初の「偵察衛星」の話題もワイドショーで取り上げられていて、こちらの方は分解能1mという性能を挙げながら、米軍の偵察衛星との能力比較などが行われていた。

　とはいえ、日本の偵察衛星が高度約490kmから地表1mの物体を見分けるとか言われても、あるいは米軍の偵察衛星のように250kmの上空から10cm程度のものを見分けるとか言われても、それだけではワタシにはどうもピンとこないのである。どのくらい「よく見えているか」がなかなかワタシにはピンとこないのである。少なくとも、ワタシにとっては「どのくらいよく見えるか」ということは、もう片目を隠す「黒いしゃもじ」とあのCの形と切り離して考えることはできないのである。つまりは、昔学校で受けた視力検査の「視力」というものが「どのくらいよく見えるか」の尺度になってしまっているのである。偵察衛星がスゴイと言われても、じゃぁどの位の「視力」なの?と思ってしまうわけである。視力4.0というアフリカ人の何倍スゴイ、と言われなければワタシにはどうも今ひとつピンとこないのである。

　というわけで、今回は偵察衛星の視力を計算してみることにした。まずは視力の定義である。視力の定義は、「識別できる最小視角（単位は分）の逆数を視力とする」となっている。だから、例えば視力1.0の場合には、直径7.5mmのCの形に刻まれた幅1.5mmの切り込みの場所を5mの位置から認識できるということになる。もし、10mの距離からその1.5mmの切り込みを識別できれば、視力は2.0であるし、21mの距離から識別できるなら、おっとビックリのアフリカ人と同じ視力4.0ということになるわけである。

　それでは、偵察衛星の場合で計算してみることにしよう。とりあえず、識別できる最小サイズをS(m),識別する物体までの距離をd(km)とすると、上の定義から視力は

1/(360*60*ArcTan[S/(d*1000)/ 2 * π])

と表される。そして、先のワイドショーで知った数字などをこの式に入れてみると、

• 高度約490kmから地表1mの物体を見分ける日本の偵察衛星 = 視力 143
• 高度約250kmの上空から10cm程度のものを見分ける米軍の偵察衛星 = 727

と、偵察衛星の「視力」を知ることができるのである。日本が誇る偵察衛星であれば、おっとビックリのアフリカ人の視力の35倍ほど上で、そして米軍の偵察衛星であればさらにその5倍以上の視力、つまりビックリ・アフリカ人の何と180倍ということになるのである。何だか、スゴイんだかスゴくないんだかよく判らなくなってしまうのである。日本がガンバッて打ち上げた偵察衛星が「スゴイ視力のアフリカ人が30倍の双眼鏡で覗いているのと同じ性能」だと言われても、偵察衛星がスゴイんだか、アフリカ人がスゴイんだか、それとも実は偵察衛星がスゴくなかったんだか、何が何だか判らなくなってしまうのである。そしてまた、ワタシの視力は日本人としては良い方の2.0位なので、アメリカの偵察衛星はワタシが400倍の望遠鏡を覗く程度のスゴさだと判るのである。まぁ、どっちにしてもピンとくるような、こないような不思議な感じだが、とにかく日本人の偵察衛星は視力が140程度で、アメリカ人の偵察衛星の視力は730程なのである。そんなことが、今回はとにかく判ったのである。

　さてさて、目がいい人が高倍率の双眼鏡を覗いていれば、私たちは当然「何が見える？」と聞くに違いない。ましてや、それが偵察衛星で、軍事行動に走る前であるならば偵察衛星から何が見えるかを丹念に調べるに違いない。もしも、私たちが高度250km偵察衛星に

「そこの街には誰かが居る？」

と訊けば、それが15cmの精度の偵察衛星ならきっとちゃんと答えてくれるに違いない。

- 今、そこには人が何人か歩いています

そこで、私たちは偵察衛星にもう少し詳しく聞いてみる。

「その人達はどんな表情を浮かべてる？」
「悲しんでる？それとも、笑ってる？」

15cmの精度では人の表情までは判らない。人が居ることは判ったとしても、今の偵察衛星では人の顔までは写らない。近くで眺めてみないことには、人の表情は判らない。

■アルキメデスのパンチラの式　

「スカート円錐」の明るさを探れ

「スカート円錐」の明るさを探れ

　以前、「ミニスカートの幾何学」として、女子高生の間などで流行っていたミニスカートの丈の短さの限界について考えてみたことがある。階段を上ろうとしているミニスカートを履いた女性（別に男性でも構わないが…）の下着が見えてしまうかあるいは見えないのかを、女性達が履くミニスカートの丈の長さから考察をしてみたのであった。

　その「ミニスカートの幾何学」の考察をした結果、ミニスカートの丈がちょうど32cmの時に、ミニスカートで下着が隠されはじめる境界線がちょうど階段と平行になる、ということが判ったのである。そして「下着が隠されはじめる境界線がちょうど階段と平行になる」結果、ミニスカートの丈が32cmより短いと下着が階段下を上る人達から見えてしまうようになり、逆にミニスカートが32cm以上の丈であればスカートの中の下着はなんと幸か不幸か見えることはないのだ、ということが判ったのである。ミニスカートをはいた女子高生が急な駅の階段なんかを上るときでも、ミニスカートの丈が32cm以上であれば、パンチラの恐怖に怯える必要はないということが判ったのであった。


　ところで、ミニスカートの中が見えてしまいそうになる場所というのは、必ずしも急な階段だけではないらしい。最近の東京の有名スポットなどでは、「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかがたくさんあったりするというのである。そして、そんな場所では、真上にいる「スカートを履いた女性」を急角度で仰ぎ見ることができて、スカートの中の下着がチラリと見えてしまうことがあるというのである。

　しかし、である。角度的にスカートの中の下着が見えるからといって、果たして本当に下着が見えるものなのだろうか？角度的には見えるはずでも、実際には人間の目には見えないことだってあるのではないだろうか。なぜなら、スカートが「私たちの視線から下着が見えるのを遮っている」のと同じように、スカートは「照明の光が下着にあたるのをも遮っている」のである。スカートの中というのはスカートに光が遮られて（たぶん）かなり暗いハズなのである。いや、実際に覗いてみた経験があるわけでは決してないので自信を持って「ハズ」と断言することはできないのだけれど、スカートの中が明るいわけはないと思うのである。もし、スカートの中が明るくなければ、仮にその中身を覗くことはできても結局暗くて何も見えないわけで、「スカートの中が（見えるくらいに）十分に明るいかどうか」が肝心だと思うのである。そこで、今回は「下着が角度的に見通せる条件」ではなくて、「スカートの中の下着が十分明るく見える条件」を考えてみたい。


　まずは、スカートをはいた女性を下の図のように簡単に示してみよう。スカートを下向きに開いた円錐として考えてみる。もちろん、スカートの中の下着はこの円錐の頂点に位置するわけだ。そして、スカートが広がる角度をΘとでもしてみることにしよう。その時、円錐の頂点にはどれだけの光が当たるものだろうか？

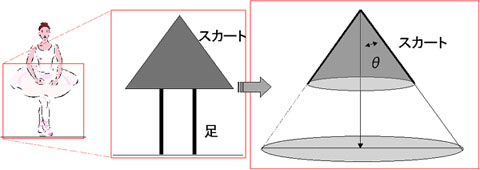　もちろん、円錐状のスカートが上からの光は遮っているわけだから、スカートの中の下着を照らす光というのは、下の床からの反射光だけである。つまりは、上の図で、「色を付けた部分の床」からの反射光のみが下着にまでたどり着き、それ以外の床からの反射光はスカートに遮られて、スカートの中を照らすことはない。ということは、「スカートの中はどれくらい明るいか？」という疑問を考えることは、それは「色を付けた部分の床からスカートの中の下着にまでたどり着く光がどれだけあるか？」ということを考えることと同じなのである。

　そしてまた、床上での光の反射に方向性が無く、光が完全に等方的に周囲に拡散するとするならば、円錐の中心（つまりはスカートの中の下着部分だ）にあたる光の量は、下の左図の色を付けた部分球の面積に比例する。つまり、「スカートの中の明るさ」は「スカートの広がり角」で決められる「部分球」の面積に比例するのである。


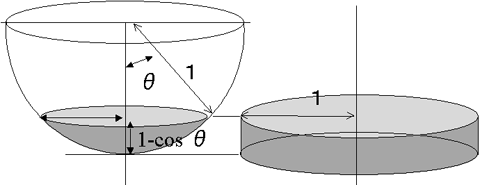　つまり、角度Θで広がるスカートの中が「どれくらい明るいか？」という疑問は、「下図で色を付けた部分球の面積はどのくらいか？」という問題に変わるわけである。「半球全体の面積に対して、スカートの広がりで決められる部分球の面積はどのくらいの割合か？」ということの答えが、それすなわち「スカートの中の明るさ」を決めているのである。

　ところで、アルキメデスが発見したように、球（もしくはその一部）の面積はその球に外接する円筒の面積に等しい。つまり、上の図の左で色を付けた部分の面積というのは、右に示したような（色を付けた）円筒の面積に等しいわけだ。ということは、右の円筒部分の面積は

円筒の面積 = 2 π (1-cosΘ)

であって、左の半球の面積が(直径=1とすると)2πだから、円錐状のスカートの中の明るさは、スカートの広がる角度をΘとするならば、「スカートの中の明るさ」は

という実に簡単な式で表されることになる。アルキメデスも、まさか自分の球と円筒の表面積に関する発見が「スカートの中の明るさを示す式（ここでは仮に『パンチラの式』とでも呼ぶことにする）」を導くために使われるとは想像だにしなかっただろうと思うが、とにかくアルキメデスのおかげで私たちはスカートの中の明るさを知ることができるのである。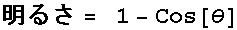

　試しに、このくアルキメデスの『パンチラの式』を使って、スカートの広がり角度Θに対して、スカートの中の明るさがどのように変化するかを計算してみると、その結果は下のグラフのようになる。このグラフは、横軸が「スカートの広がる角度」で、縦軸が「スカートの中の明るさ」を示している。周囲の「照明に照らされている床」の明るさを１とした時の「スカートの中の明るさ」を示しているのである。

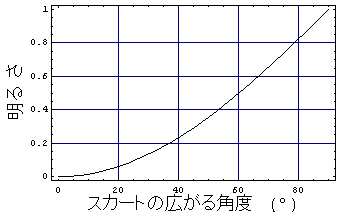　基本的にはスカートが広がるにつれて「スカートの中の明るさ」は明るくなるわけであるが、このグラフを眺めてみると、スカートの広がる角度が20°を超えるあたりから次第にスカートの中が明るくなることが判るだろう。例えば、スカートの広がる角度が30°の時には、スカートの中は「床の明るさの10%程度の明るさ」しかないが、スカートの広がる角度が60°にまで広がれば、スカートの中は「床の明るさの半分程度の明るさ」になる、ということが判るわけだ。


　ところで、人間の目というものは「見るものの明るさ」に合わせて順応する。例えば、暗いものを見るときには目の感度は自動的に上がる。だから、スカートの中がほのかでも明るかったならば（例えば床の明るさの5%程度にでも明るければ）、自動的にその明るさに目が順応してスカートの中が見えてしまうかと思いきやそうはいかない（ハズだ）。なぜなら、人間の目は明るいものを見る時には、目の感度が逆に自動的に低下してしまうからである。スカートの中以外の明るい場所（例えば照明や、照明に照らされた明るい壁）だって、自動的に視界の中に入ってくるわけで、目の感度はそういう明るい部分に自動的に合ってしまうハズなのである。

　例えば、下の画像は周りの明るさに対して、

1. 5%の明るさ
2. 10%の明るさ
3. 20%の明るさ

を持つ三種類のロゴである。この三つの画像を眺めてみれば、明るさが5%のものはなかなか判別しにくいが、20%以上の明るさのものであれば比較的容易に判別できることが判るだろう。明るいものが視野に入っている限りは、人間の目は「一番明るいものの10%以下程度の明るさのモノ」はなかなか識別することはできないのである。

5 %

10 %

20 %

　ということは、先のグラフで「スカートの中の明るさ」が10%を超えていないと、つまりは周囲にある明るい床（や照明や壁）などの明るさの10%を超えているくらいでないと、スカートの中が仮に幾何学配置的に見える条件であったとしても、実際には目の感度的にその中のようすを判別することができないに違いないのである。その場合、おそらく明るい床や壁の明るさに目の感度が合ってしまい、ほの暗いはずのスカートの中は真っ暗にしか見えず、幸か不幸かスカートの中身は識別することができないハズなのだ。

　というわけで、先ほどのグラフに「識別できる明るさか否か」を書き入れてみると、次のグラフのようになる。

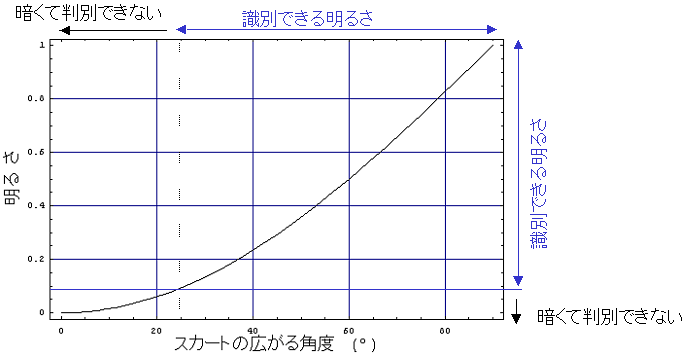　つまり、スカートの広がる角度が25-30°を超えていないと、スカートの中身は周囲の床や壁の明るさに比べて相対的に暗すぎて人間の目ではおそらく見ることができないのだ。


　例えば、スカートの広がる角度が30°以下に制限されるようなタイトスカートを穿いて、明るい壁や照明などが視界にどうしても入ってしまうような場所にたたずんでいる限りは、もし仮にスカートの中を覗かれたとしてもスカートの中は（人間の目からすると）真っ暗で何も見えないわけで、スカートの中身を見られたりするような被害にあうことはまずないだろう、ということが先のアルキメデスの『パンチラの式』から判るわけなのである。「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかであったとしても、背後に明るく輝くものがある限りには、見る人の目を眩ませることができて、スカートの中身は安全なわけである。

　ところが逆に、床が白かったりして明るいクセ（つまり下からの照明が強いクセ）に、周りに明るい壁や照明が何故かあまりないような場所がもしあったとして、もしそんな場所で（下から）スカートの中を覗かれたりしてしまうと、（下から覗く人の視界に入る）周囲の明るさに比べてスカートの中が十分明るく見えるせいで、しっかりとパンツの模様をチェックされてしまうということになるだろう、ということも予想することができてしまうのである。だから、そんな場所をもしも短いスカートをはいて歩かなければならないような場合には、例えば何かの「ピッカピッカ輝く光りモノ」でも身につけて、その光りモノの明るさを「スカートの中身をのぞこうとするスナイパー」の視界に入れて、彼らの目を眩ませてしまえば良いだろう、というアルキメデスの知恵さえ授けてくれるのだ。

　
　ところで、今回は「スカートの中の明るさを示す＝パンチラの式」を考えてみたわけであるが、この式は考えるまでもなく実にアブナイ式である。パンチラの被害防止に役に立ちそうな気もするし（全然役に立たないような気もするが）、逆に単なる「パンチラの科学」になってしまっているような気もしてしまう。「スカートの中身をのぞこうとするスナイパー」の魔の手から逃げるためのバイブルになるような気もするし、「スナイパー」のための手引き書になってしまいそうな気もする。ギリシャ神話で、あらゆる災厄が入っていたという箱がパンドラの箱だったけれど、このパンチラの式だって案外そんなパンドラの箱のような、色んな災厄の元になってしまうものかもしれないのである。しかも、パンドラの箱の場合には最後に箱の中に『希望』が残っていたわけでまだ良い（？）のである。しかし、アルキメデスの『パンチラの式』の場合には「スカートの中にだっては『希望』が入っているのだぁ」などと口に出したりしたら単に変態扱いされてしまうだけなわけで、そこはパンドラの箱よりもずっとたちが悪いのである。つまりは、科学もアルキメデスの『パンチラの式』も使う人次第なのである。

■トイレットペーパーの直径と平均的ウンコ長の関係式　

　誰かこの仮説

トイレットペーパーの直径はそれぞれの国の平均的ウンコ長に比例するのではないか？数学的に。

の真偽について考えてみて欲しいもの。海外のトイレットペーパーの長さって…、そう言えば覚えてないぞ。というか、気にしたことがなかったぞ、と。