1999-07-05[n年前へ]
■目に映る明るさって何ですか? 
君は天然色
前回、デジカメ画像をスクリーンセーバーにしたい-記念写真を飾ろう - (1999.06.30)
を作るために、いくつか調べ事をした(ホントはずっと昔に)。それについてまとめておきたい。
調べたことは、
- カラーから白黒への変換はどうする?
- セピアカラーって一体何だ。
- セピアカラーへの変換はどうやろう?
カラーから白黒への変換はどうする? どうしよう? これは結構難しい問題(結果的にやったことは簡単でも、プロセスとしてはすごく難しい)だ。そうそう白黒の世界を見たことのある人はいないだろう。特殊な状況下(たとえば、すごく暗い所とか)では色を感じないこともあるだろうが、普通の世界は天然色である。フルカラーの世界だ。そもそも明るさって一体何だ?(明快に答えられる方教えてください。) 例えば、下の図で明るい順番はどうなっているだろうか?自信を持って答えられるだろうか。
 |
とグチを言っていてもしょうがないから、決めてしまおう。うす暗い(1lx程度)部屋で景色を眺めてみよう。その時見える世界が、明るさの世界だ。そこには色など存在しない。確かめて欲しい。今回は、とにかくそれを「明るさ」の尺度としてしまおう。
(興味ある方は明るさを測ろう- 新技術の女神 -(1998.11.13)もご覧下さい)
次に明るい部屋へ移動する。そこでは、新たなものが加わる。それが「色」である。ということで、「明るさ」+「色」で世界を表現することにしよう。
いきなりではあるが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。
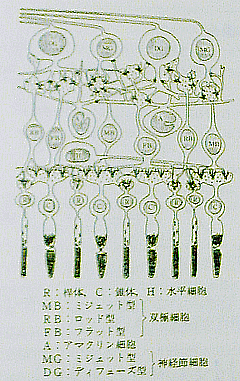 「視覚と画像」 大頭・行田 著 森北出版より |
それでは、明るい部屋で感じる色はどうなっているだろうか。色を感じる錐体の中には波長感度の異なる3種類の視物質がある。それぞれの波長感度を以下に示す。
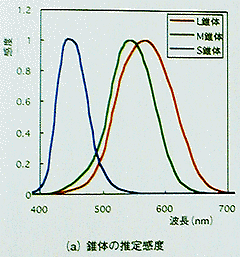 CQ出版 洪 博哲著 「お話・カラー画像処理」より |
次に、それらの3種類の視物質による錐体が組み合わさった時の波長比視感度を以下に示す。点線で示してあるほうは比較的暗い場所での波長比視感度なので、今回は無視して欲しい。
 「視覚と画像」 大頭・行田 著 森北出版より |
後は、このグラフを元に赤、緑、青の3点で重み付けしてやれば良いだろう。
というわけで、グレー化のために使っているのはこの式だ。
- Red: ptr[2]
- Green: ptr[1]
- Blue: ptr[0]、として
やっと、ここまで辿りついた。結局使うのはこんな簡単な式なんだ、っていうツッコミは無しにして欲しい。同じ式を使うのでも、私はそこまでのプロセスも重視したいのだ。
さて、こういった色を扱う話題であれば、脇色彩研究所のWEB(http://www.mmjp.or.jp/rwicp/ )中から
- 色に対する感じ方(眼とフィルム)( http://www.mmjp.or.jp/rwicp/data106.html )
- カラーフィルムの特性と色再現( http://www.mmjp.or.jp/rwicp/filmirosai.html )
- 明るさの見え方(明暗対比)( http://www.mmjp.or.jp/rwicp/data506.html )
- 色覚、眼の色に対する感じ方( http://www.mmjp.or.jp/rwicp/data509.html )
また、文中でも書いたが、「明るさとは***ということだ」と明快に答えられる方は私に是非教えて頂きたい。もし、素晴らしい答えが頂けたら、粗品(言葉通りの)を進呈しても良いと思っているくらいだ。
なお、以下のような答え方は遠慮致したい。
例1:
私 「液体と固体はどう区別するの」
A 「融点を境にして上と下」
私 「....」
例2:
私 「クジラは哺乳類、魚類どっち?」
A 「卵生まないから哺乳類」
私 「...」
1999-08-08[n年前へ]
■瞳の中の真実 
目の屈折率を調べよう
先日、近所の海へ行ってきた。水中メガネで覗いているとまるで熱帯魚みたいな魚が泳いでいて素敵なのだ。水中メガネを使うか使わないかで、海の楽しさは雲泥の差である。水中メガネで覗いてみると、裸眼の時とは別世界のようにくっきり見えるのである。
 |
さて、「水中視の光学」と言えば、物理の散歩道の「アユと泳ぐ」(新物理の散歩道-第2集- 中央公論社)に詳しく面白い考察がされている。本WEBでもScrapsにて「焦点」ということを考えたばかりなので、「アユと泳ぐ」と同様の解析を「できるかな?」風に行ってみたい。光学シミュレーターを作ってみたいのである。そのために、まずは人間の目の中の屈折率を調べなければならないだろう。というわけで、今回は下調べ編である。
それでは、人間の左目の水平方向の断面図を調べてみる。
 |
この中で普通のカメラでいうレンズの役割を果たしているのはどこだろうか。レンズの部分を赤く塗るとどのようになるだろうか?下に並べた3つのうちどれだと思われるだろうか。
A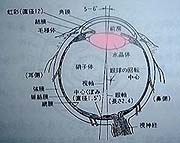 | B | C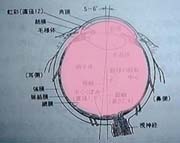 |
まずは、目の中の物質の屈折率を調べてみると、以下のようになる。
| 場所 | 屈折率 |
| 角膜 | 1.376 |
| 眼房 | 1.336 |
| 水晶体 | 1.386 |
| 硝子体 | 1.336 |
空気(15℃の乾燥空気)の屈折率はほぼ1.0であるから、空気と比較するならば、目の中の物質はほぼ同じ屈折率を持つといっても良い。角膜も眼房も水晶体も硝子体も同じ屈折率を持つとして良いだろう。すなわち、大雑把な近似においては図.2のCに示したようなピンク色のレンズがあるとして良い。つまり、目全体がレンズであり、レンズ面に焦点を結ぶようになっているのである。水晶体は若干の補正を行うに過ぎない。レンズの焦点はレンズから離れた場所にあるはずと思っている人もいるかもしれないが、レンズの表面に焦点があるものも実はよく使われている。
さて、人間が水の中に入るとどうなるだろうか?水は1.333(589.3nmの波長の光に対して)の屈折率を持つ。これは人間の目の中の物質の屈折率とほぼ同じである。水を主体として出来ている人間なのだからこれは当然だろう。しかしこれでは、目は光を屈折させることはほとんどできなくなる。そのため、水の中に入るときには水中メガネなどで目の回りを空気で満たしてやることが必要なのである。
本題からははずれるが、資料を眺めていると、面白いグラフが目に入ってきた。人間の目の断面方向の視細胞個数の分布を示したものであり、錐体と桿体を個別に示してある。「盲点」なんかも図中にある。
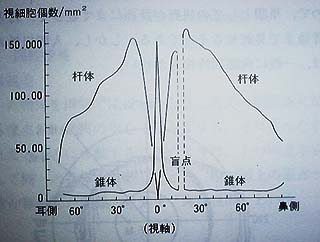 |
目に映る明るさって何ですか? - 君は天然色 - (1999.07.05)
の回に錐体と桿体については触れたが、桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上で働く。従って暗いものを見るには桿体の働きが重要になるわけだが、上のグラフは桿体が視点の中心にはほとんど存在していないことを示している。
従って、暗い所でものを見る際には、視点の中心では感度が足りなくなりやすいことがわかる。これまで、暗い星を眺めるときに視界の中心で見ようとすると見えないのだが、少し視点をずらしてやると見えるような気がしていたのだが、それは気のせいでは無かったようである。
さてさて、資料集めも終わったので「瞳シミュレーションソフトウェア」の開発に着手したいと思う。もちろん、時間がかかるのはいつものことだ。すぐにはできないけどね。
1999-08-09[n年前へ]
■色を伝える時に、考え忘れていたこと(色弱と色空間 その1) 
We can work it out!
オプトニューズ (1999) No.4の光の話題に三楽病院の岡島修氏が「レーザポインタと色覚異常」という小文を書いている。色弱の人の感じ方とプレゼンテーション(特にレーザポインタの色)に関する提言である。それを読んであることを思い出した。何年か前、Labofinder(Macintoshを科学分野で使うユーザーグループ)でプレゼンテーションについて特集していた発表会だったと思う。どなたかが発表を行った後に、次のような質問があった。
「私は色弱なのですが、プレゼンテーションを行う際に使う色などについて、そのような人を意識して作成されているでしょうか?」
恥ずかしいことに、私はあまり考えたことがなかった。そして、本WEBを作るに際してもそういった点はおろそかになっていると思う。そういう自分自身への反省を込めて、色弱と色空間について考えてみたいと思う。
まずは、色弱に関する情報を調べよう。
- COLOR HANDICAP( http://www.sakuranet.or.jp/~tks/color/text/ )
- からーふぃくしょん( http://sun.endless.ne.jp/users/tanafic/ )
- Dr.MeMeの おめめ講座 (http://www.so-net.ne.jp/vivre/eye/ )
それでは、私なりの理解と考察を始めてみたい。
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
の回で触れたが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。この内、色(すなわち光の波長方向に関する感じ方)を感じるのは、錐体の働きによるものである。錐体には3種類有り、
- L錐体 -> 赤
- M錐 -> 緑
- S錐体 -> 青
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
を参照のこと)。それらの錐体に異常がある時に、色弱もしくは色盲が発生する。
| L錐体 (赤) | M錐体 | S錐体 | 先天性色覚異常の分類 |
| O | O | O | 正常 |
| X | X | X | 桿体1色覚 (全色盲) |
| O | X | X | 錐体1色覚 (赤) |
| X | O | X | 錐体1色覚 (緑) |
| X | X | O | 錐体1色覚 (青) |
| X | O | O | 第1色盲 (赤色盲) |
| O | X | O | 第2色盲 (緑色盲) |
| O | O | X | 第3色盲 (青色盲) |
| OX | O | O | 第1色弱 (赤色弱) |
| O | OX | O | 第2色弱 (緑色弱) |
| O | O | OX | 第3色弱 (青色弱) |
この図中でOは正常、Xは欠損、OXは機能低下である。
M,L錐体に関する異常はX染色体劣勢遺伝をする。また、錐体1色覚、および、S錐体に異常がある第3色盲・第3色弱は比較的少ないという。
それでは、これらの錐体に異常があるとどのような色を識別できなくなるのだろうか? 私は先に挙げたようなWEBを読んだくらいの知識がないので、数学的な考察をおこなってみる。現実をよく知らないため、実際の症例とはかなりの違いがあるかもしれない、ということは先に断っておく。
現実の症例の参考としては、岡島修氏の「レーザポインタと色覚異常」中に挙げられているCIEXYZ表色系における強度色覚異常者(第1異常、および、第2異常)の混同色を用いる。その図を加工し、XY色度図を重ねたものを以下に示す。それぞれの図において、白い直線上の色を混同してしまうのである。
 |  |
今回は、通常の(Red,Green,Blue)データを基本として考える。PCなどで表示を行う際に一番よく使うからである。任意のRGBデータをCIEXYZ表色系に直すためには、
WEBページは会社の顔色 -WEBページの色空間を考える2- (1999.04.26)
で用いたハイビジョンTVの色空間を例に用いて、
- X= 0.412391R + 0.357584G + 0.180481B
- Y= 0.212639R + 0.715169G + 0.072192B
- Z= 0.019331R + 0.119195G + 0.950532B
- x=X/(X+Y+Z)
- y=Y/(X+Y+Z)
それでは、通常、第1色盲(赤色盲)、第2色盲(緑色盲)の3種類についてxy色度図の計算例を示してみる。ある錐体に異常が存在する場合に、どのような色空間が再現されるかの計算を行ってみる。通常のxy色度の位置において、ある錐体の刺激を無くした場合に色がどう変化するかを示したものである。であるから、第1色盲(赤色盲)、第2色盲(緑色盲)においては通常使われるxy色度図とは異なるものになる。また、ここで示した色が色弱の人が見ている色という意味でもない。
単純に、ある錐体が得るであろう情報を無くしたときに、情報の識別がどのように困難になるかを確認した、と言った方がいいかもしれない。
また、本来3錐体の波長感度特性はRed,Green,Blueの単波長というわけでもない。しかし、今回は簡単のために、3錐体の波長感度特性はRed,Green,Blueの単波長であるという仮定の元に計算を行っている。そのため、かなり現実とは違う結果になっている。近々、きちんとした計算をするつもりである。
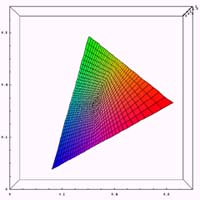 |  | 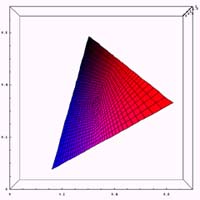 |
ここでは、Z方向(明るさ方向)に対して無視を行っているので、かなりの誤差が存在すると思う。また、計算の中で一つの錐体に異常があるときの、RGBデータの再配分を計算する部分に極めて大雑把な近似をおこなっているので、その部分でも誤差が大きいと思う。
また、Red,Green,Blueの三色により色空間を形成しているため、各点を頂点とする三角形内に色空間は収まることになる。
この計算結果を眺めながら、岡島修氏の「レーザポインタと色覚異常」中に記述されている色弱における混同しやすい色の例、
- 第1色盲
- 赤と黒
- ピンクと青
- 第2色盲
- 赤と緑
- オレンジと黄緑
- 緑と茶
- 青と紫
- ピンクと白
- 緑と灰色
例えば、通常の色空間において赤(すなわち右上)の場所を第1色盲の色空間の中で見て欲しい。黒との識別が困難なのは一目瞭然だろう。また、下の図に示すように、通常の色空間でピンク(1)と青(2)が第1色盲の色空間の中でどうなっているかを見れば、
 | 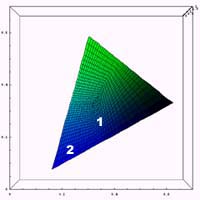 |
これも1と2の識別が困難であることが容易に想像がつく。第2色盲でも同じように見てみて確認して欲しい。
なお、上の図中で中心部が暗くなっているが、それはグリッド線のためであり、本来の色はもっと白っぽい色である。また、今回は岡島修氏の「レーザポインタと色覚異常」中の図と比較するために、CIExy色度図を用いたが、もともとxy色度図は人間の感じ方とは結びつけにくい。いずれ、均等色空間における解析を行うつもりである。また、先に記述したようにきちんと錐体の波長感度特性を考慮に入れた計算をするつもりである。今回はあくまでごく簡単な実験である。
というわけで、今回は色弱の方がどのような色空間を感じているかを考察してみた。今回の話中には色々間違いもあると思う。なにか訂正すべき情報を見つけてくださったら、教えて欲しい。
画像出力に携わる方でこのWEBをご覧になっている人もいるはずだ。色を正しく伝えることを日夜考えている人もいるだろう。しかし、色を正しく伝えることを考えるときに、考え忘れていることはないだろうか? 「正しい伝え方」は、誰にとって「正しい」のだろうか?私達が当然のように感じている色についても、異なる感じ方をする人のことを考え忘れてはいないだろうか?
そういった人は少数だと言われる方もいるかもしれない。しかし、あなたが当然の権利のように享受しているものは果たして全ての人が得ているものだろうか? もしかしたら、その権利を享受している人の方が少数派であるものもあるのではないだろうか?
やることは至極簡単なことだ。技術的に言うならば、人の知覚も「デバイスの一部」として考えた際に、「人の知覚」が数種類あるものとして、異なるデバイス間のカラーマッチングを考えれば良いだけのことだ。もちろん、一筋縄ではいかないだろうが、得られるものの大きさからしたら、やってみる価値はあるだろう。
プレゼンテーションソフト、あるいは数多くのソフトウェアにそういったことをきちんと考えたテンプレートが現れ、WEBサイトの色、画像機器のカラーマネジメントにそういった「全ての人(健常者と呼ばれる人のモデルだけでない)の感じ方まで含めたカラーマッチング」が適用されていく日も必ず来るはずだ。もしかしたら、このWEBサイトに来ている人の中には、今すぐにでもそういうことを始めることが出来る人もいるかと思う。果たして、そんなことが「できるかな?」と思われる人もいるかもしれないが、きっとできる筈だ。
こういったことは色覚に限る話ではないと思う。考え忘れていることは数多くある。できることも数多くある、と私は思う。
1999-08-10[n年前へ]
■WEBページは会社の心 (色弱と色空間 その2) 
WEBページのカラーを考える 3
前回、
で色弱の人の感じる色空間について少し考えてみた。また、などで、WEBページの配色やレイアウトからその会社自身について考察してみたことがある。今回は、それらを組み合わせてみたい。前回考えたやり方(ある錐体の情報を無くした際に得られる色空間をシミュレーション計算する)で色々なWEBページを解析してみるのだ。その結果として得られるものは、会社の「心」を示しているかもしれない、と思うのである。
まずは、そのためのプログラムを作成してみた。といってもごく簡単なユーティリティーである。画像ファイルを読みこみ、RGBデータの内任意の1チャンネルの情報を削除した画像を作成するのである。
実作成時間は15分程である。使いやすさはほとんど考えていないし、ボタンの押す順番によってはプログラムが簡単に落ちるというゲーム代わりにもなるものである。もし、使いたい人がいるならば、そこらへんはちゃんと直すつもりだ。それでも使うのは簡単だとは思う。今のところ、私以外に使う人がいるとも思えないので、こんなもので構わないのだ。
簡単に今回作成したプログラムTrueColorの動作画面を説明する。
 |  |
 |  |
TrueColorは画像ファイルを読みこみ、
- RGBの内の1チャンネルを全て0にする
- RGBの内の1チャンネルを他の2チャンネルの平均値にする
また、画像読みこみに関してはSusieプラグインに対応している。
使う人がいるとも思えないが、一応ここからダウンロードできる。
truecolor.lzh 360kB
それでは、各社のWEBページを調べてみる。各社のWEBを見た上で、一番識別が困難になりそうな条件で解析を行ってみた。その結果、前回調べた7社中(ただし、今回は日本国内の会社のみ)では、ある1社以外は何の問題もないように思われる。大丈夫と思われる例を示してみよう。これはアップル株式会社である。
 |  |
特に見にくい個所は見当たらない。それは他の会社についても同様であり、ある1チャンネルの情報を欠如させても特に識別しにくい個所は見当たらなかった。
さて、問題があると思われる1社はどこだろうか? そう、RICOHである。ただでさえ、見にくいデザインなのであるが赤のチャンネルの情報を削除すると文字の識別が困難になるボタンがある。このボタンのデザインは非常に見にくい。
 |  |
RICOHは内容的には非常に素晴らしいWEBなのだから、WEBの色にももう少し気を配ると良いと思う。内容が伝わらない可能性があるというのは、非常にもったいないと思う。
さて、他のWEBも調べてみよう。気を配っているはずの厚生省だ。
 |  |
1箇所ハイライト部分が識別不能(ハイライトになっていることを)であることを除けば、問題は無いようである。
さて、他のWEBを調べるなら当然本WEBについても調べなければならないだろう。
 |  |
背景に色をつけているので、若干見にくいとは思うが、うーん、落第かな... どうしたものか。
1999-08-20[n年前へ]
■色空間の世界へ (色弱と色空間 その3) 
Someday
今回は、
色を伝える時に、考え忘れていたこと(色弱と色空間 その1) - We can work it out! - (1999.08.09)
で行った計算を少し改良し、なおかつ色空間の世界を自由自在に動かしてみたいと思う。今回のメインは「立体グリグリ」のテストである。
まずは、前回と今回の計算の違いは、
- 前回はL,M,Sの各錐体の波長感度特性はRed,Green,Blueの単波長であるという仮定の元の計算
- 今回はL,M,Sの各錐体の波長感度特性はRed,Green,Blueの単波長とは異なるという条件での計算
- X= 0.412391R + 0.357584G + 0.180481B
- Y= 0.212639R + 0.715169G + 0.072192B
- Z= 0.019331R + 0.119195G + 0.950532B
- l = 0.16*X + 0.54*Y - 0.033*Z
- m = -0.16*X + 0.46*Y+0.033*Z
- s = Z
それでは、通常のRGB色空間と第1色盲(赤色盲)のRGB色空間を以下に示してみる。今回はMathematicaの出力をJavaAppletで動かすことができるLiveGraphics3Dを使用している。そのため、RGB色空間をグリグリ動かすことができる。それどころか、ステレオ画像にしてグリグリ動かすこともできる。ステレオ画像の見方は交差法である。ぜひ、試してもらいたい。
下のグラフの操作方法は
- 操作 = 作用
- マウス左ボタンドラッグ = 回転
- シフトキー + 垂直ドラッグ = ズームイン・アウト
- シフトキー + 水平ドラッグ = 垂直軸についての回転
- コントロールキー + 垂直ドラッグ = 焦点距離の変更
- マウス右ボタン垂直ドラッグ = 部品除去
- "s"キー = ステレオ画像作成
PageLiveGraphics3D
( http://www.nikonet.or.jp/spring/sanae/LiveGraphic3D/LiveGraphic3D.htm)
を参考にして欲しい。それでは、RGB色空間(ハリボテバージョン)を自由自在に動かしてみよう。
|
|
どうだろうか? RGB色空間を自由自在に動かせただろうか? 立体グリグリはできただろうか? 「ハリボテでつまらない」なんていう文句がある人もいるかもしれないが、気が向けば立方体の全面について描画を行うよう変更するつもりである。
こういった、Javaなどを使用した立体表現は表現力が非常に高い。しかし、読み手によっては必ず見れるとは限らないところが難しいところである。読み手を限定してしまう可能性が有る。それは、まさに色覚異常に関する問題と同じである。
TVが白黒放送からカラー放送に移行する当時は、カラー放送においても白黒TVでもきちんと識別できる色を考慮しながら放送しようとしていた、と聞く。白黒TVで観ている人が困らないようにである。しかし、現在はどうだろうか? 白黒TVで観ている人のことを考慮したTVなどほとんど無いのではないのではないか?
TV放送に限らずWEB、プレゼンテーションなどにおいて、最新の可能性と広い互換性を両立させていくためには、他の人を配慮する力が必要だと思う。そういう点においても非常に優れ、私がとても好きなWEBサイトが今日から一時停止してしまった。非常にさみしい。
それでは、今回の色空間自由自在はこんな所で終わりにしたい。