1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
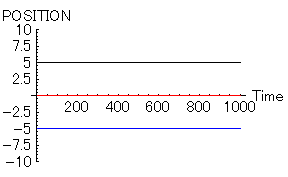 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
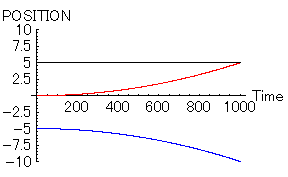 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
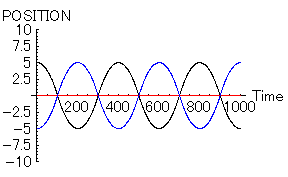 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
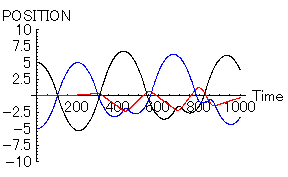 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)
2000-02-05[n年前へ]
■恋の固体物理学 前書き編 
シリコン・エイジの恋
これまで、様々な「恋の形」について考えてきた。古くは、
であったり、あるいは、であったりした。最近の「恋の力学」シリーズでは、初めに男と女の間の「恋の二体問題」を考え、そして二人の男と一人の女の間の「恋の三体問題」を考えてきた。しかし、それらの「恋の力学」が取り扱ってきたものは、ごく少数の登場人物により演じられる物語を解析したものである。また、特に「男」と「女」の間に性質的な差がないものとして、解析を行ってきた。
このような解析の前提条件、
- ごく少数の登場人物
- 「男」と「女」の間に性質的な差がない
- 数え切れない多数の人物が登場し
- 「男」と「女」の性質の間に差がある
例えば、
- 「男」も「女」も結構人数はいるのであるが、その数がかなり違う。
- 「男」が諸星あたるのように、やたら行動力があるが、「女」の方ははなかなか動かない
- 恋人達に何かのショックを与えると分かれてしまう。
- その場の雰囲気でカップルになっちゃった
こういった色々なことが「恋の物理学」では起きる。しかし、
で書いたように、夏目漱石の時代に作り上げられた「恋の力学」ではそのような現象の解明は困難である。そこで、新たな「恋の科学」の分野を作り上げ、そういうことについて考えを巡らせていきたい、と思う。とはいえ、いきなりやるのは私には難しい。そこで、まずは解析のための準備をしていきたい。
というわけで、本シリーズは題して、「恋の固体物理学」である。先に述べたような「不均等な恋の挙動」を例えば半導体工学のような固体物理学のテクニックを用いて解明したいと思うのだ。割に単純な「恋の力学」シリーズとは別に、「恋の固体物理学」シリーズを始めたいと思うのである。
普通に考えるならば、 - 何故「恋」の挙動解明に、半導体工学? - と思われるかもしれない。確かに、唐突であるとは思う。しかし、考えてみればそれほど不自然ではない。何しろ、現在はシリコンの時代であると言われる。
プラスティック・エイジを経て、現在はシリコン・エイジが世界を支配している。シリコン= 半導体技術により、世界は動いているのだ。そうであるなら、「恋に動かされる人」の挙動も、、半導体技術を用いることにより解き明かすことができるかもしれない。(いや、もちろん今考えた理屈である。簡単に言えば、こじつけである。)
そしてまた、「恋」は一般的に(例外はあるが)
- 男
- 女
- プラスの「正孔(ホール)」
- マイナスの「電子(エレクトロン)」
- 「男」も「女」も人数はいるが、その数がかなり違う。
そのような理屈で半導体工学と関連づけながら、「恋の固体物理学」について考えてみたいと思う。
このシリーズは少しヘビー(私にとって)なので、今回は前書きのみに留めたい。これから公開予定の作品群を紹介すると、
- 恋の固体物理学 恋のバンドギャップ編 - 彼女の防護壁を突破しろ! - (仮称)
- 恋の固体物理学 恋のドーピング編 - 女子校の教師はパラダイスか? - (仮称)
- 恋の固体物理学 恋の熱励起編 - 別れたくなかったら頭を冷やせ - (仮称)
- 恋の固体物理学 恋のp-n接合編 - 一方通行の恋の行方 - (仮称)
- 恋の固体物理学 恋のEinsteinの関係式編 - 本気と浮気の境界線 - (仮称)
まだまだ続く「恋の力学」シリーズと共に「恋の科学」を作り上げていきたいと思う。
2000-04-21[n年前へ]
■オレにはヤツらが見える 
スギの花粉は「見える?見えない?」
少し前まで、スギ花粉が飛びまくっていた。スギ花粉症の人にとっては、とても苦しい季節だろう。私の家族も結構スギ花粉症にかかっている。ということは、私もいつか苦しむことになるのだろう。いや、むしろブタ草を主因とする小児喘息で酸素吸入を繰り返した私であるから、まだかかっていないのが不思議なくらいである。
さて、私の勤務先でもスギ花粉で憂鬱になっている人は多い。ヒドイ(もちろん症状が)人などは、この季節になると、
「今日はスギ花粉がいっぱい飛んでいる。」と囁き始めるのである。毎日、である。そういう時に
「オレにはヤツらが見える。」
「ヤツらがオレに襲いかかってくるんだ。」
「誰かがオレの頭に電波を飛ばしてくる、という話に似ていますね。」などとチャチャを入れると大変である。
「スギ花粉症にかかっていないやつに何がわかる!」と言われてしまうのである。いや、確かに私には見えないのだ。ピンクの象が飛んでいるのが見えないように、スギの花粉も私には見えないのである。
「オマエら、スギ花粉症にかかっていないものに、所詮ヤツらは見えないんだ!」
「ほら、あそこにスギ花粉が見えるだろう」と指さす辺りを眺めても、私には何も見えない。ただ、ボンヤリした霞が見えるだけである。仕方がないので、そんな時には、なおさら
「普通の人には見えないところなんか、ホント電波と同じですね。」と言ってみたくなる。いや、私の性格からするともしかしたら言っているかもしれない。うん、言っているだろう。それどころか、
「その花粉を飛ばしてくるのは、宇宙人かナニかですか?」と、火に油を注ぐようなことを言っているに違いない。しかし、その性格は親譲りだ(坊ちゃんじゃないけれど)。
それはさておき、
「オマエら、スギ花粉症にかかっていないものに、所詮ヤツらは見えないんだ!」と言われているだけではくやしいので、私もスギ花粉を見てみたいと思う。当然である。あらゆるものを「目に見えるかたち」にするのが私の好みである。というわけで、可視化シリーズの始まりである。いや、可視化という言葉はどうも小難しく感じるので、名前を改めて「見える?見えない?」シリーズの続きである。これまで、漱石の小説、星の王子さまの内側、透け透け水着、ミニスカートの内側…などさまざまなものを「目に見えるかたち」にしてきたが、その続きというわけだ。
今回登場する、秘密道具はコイツである。
 |
この道具は、チンダル現象を利用して微粒子を可視化してくれるのだ。というと、小難しく聞こえるかもしれないが、とても簡単な原理である。光を微粒子に当ててその反射光を目で見るだけである。もちろん、微かな反射光を捉えるわけであるから、
- 微粒子からの反射光以外は目に見えないようにする
- ボケを小さくするために、絞りはできるかぎり小さくする
さて、それではコイツでスギ花粉(らしきもの)を見てみよう。暗闇に浮かぶ「スギ花粉(らしきもの)」が見えるのだ。
 |
こういった感じでスギ花粉(らしきもの)を可視化することができる。といっても、この微粒子がスギ花粉である保証は「全く」ないのであるが、あえて「スギ花粉(らしきもの)」としておくことにする。ちなみに、この画像もスギ花粉の最盛期に撮影したものである。とりあえず、こうすればスギ花粉症のあなたの敵、すなわちヤツらを目にすることができるのだ。敵であるターゲットの姿を知らずして戦うことはできないだろうから、スギ花粉症のあなたにはこの実験をすることを強く勧めたい。この画像はデジカメで撮影したのだが、実際に人間の目で見ると、ものすごい数の微粒子が飛び回っているのがわかる。今回見えた画像がスギ花粉かどうかはさておき、こういった微粒子は部屋の中ではほとんど見られない。しかし、戸外ではかなりの数の微粒子を目にすることができる。
もう一枚、参考までに示しておく。微粒子が動き回る様子が実感できるはずだ。こういう微粒子があなたの鼻や喉の粘膜に襲いかかってきているのだ。
 |
これらの飛び回る「スギ花粉(らしきもの)」を撮影したmpeg動画(115kB)をここにおいておく。スギ花粉症の人はぜひ敵であるヤツらを自分の目で確認して頂きたい。
さて、「可視化」シリーズ、改め、「見える?見えない?」シリーズはこれからも続く。ありとあらゆるものの「見える?見えない?」境界線を追求したい。どんなにクダラナイものであっても、あらゆるものを「目に見える」ようにしていきたいと思うのである。
2000-05-12[n年前へ]
■メガネの内側にある歪み 
隠れたストレスに光を当てろ
また、可視化の話である。いや、自分でも忘れていたが、「可視化」改め「見える?見えない?」シリーズである。今回はメガネの内側にある「歪み」、隠れたストレスに光を当ててみたい。そして、そこに何があるかを見てみたいのである。
私の眼はどうも明るさに弱い。やたら太陽の光が眩しく感じることが多い。といっても、単に私のガマンが足りないだけかもしれない。あるいは、睡眠不足のせいかもしれない。そして、私は同時に暗さにも弱いのだが、こちらは単にビタミン不足による鳥目だろう。
そういうわけで、明るいのに弱いので車を運転する時には大抵サングラスをかけている。サングラスは何本も持っているわけだが、最近のお気に入りはこれである。
 |
これは、偏光フィルター機能付のサングラスである。偏光というギミック付のところがお気に入りの理由である。以前、
で書いたように、偏光フィルターがあれば色々なものの反射光のみを遮ったりすることができる。例えば、下の右側の写真では左の写真に比べてガラス表面の反射光が減少していることがわかるだろう。これは偏光フィルターの作用のせいである。 |  |
これと同じように、偏光フィルター機能付のサングラスを使えば色々な反射光を防ぐことができる。例えば、通常は反射光などで車のフロントグラスの内側にいる人の姿はよく見ることができない。しかし、このメガネをかけていれば、反射光に邪魔されずフロントグラスの内側を見通すことができるのである。もう、対向車なんてまるでフロントグラスがないかのようである。
この偏光フィルター機能付のサングラスは、通常「釣り」などで用いられるものだ。水面の反射光を防ぐことにより、水中の魚の姿などを見やすくするためのものである。結構、海の近くに住んでいる私にはうれしい機能である。
このサングラスをかけている時に、ふとある実験を思いついた。普段は透明にしか見えない「普通のメガネ」の影に隠れたストレスを目に見える形にしてみようと思ったのである。よく、「メガネの奥にストレスが隠れている」というが、そのストレスを見て取れる形にしようと思うわけだ。
そこで、新婚ホヤホヤの「夜の帝王」I田氏(関係ないが、I田氏から「Hirabayashiさん、小杉のメーリングリストで-できるかな?-の話題が出てましたよ。」と言われた時はビックリした。とりあえず、どなたか知らないが、メーリングリストで紹介して頂いた武蔵小杉勤務の方には一言お礼を言っておきたい)にメガネを借りてみた。このメガネをじっくり眺めてみてもらいたい。
 |
この透明なメガネの奥に何か見えるだろうか?そこに「歪み」は見えないだろうか?「透明だから、何も見えないだろう。」という人もいるだろうが、あるグッズを使うと、もう明らかに見えてくるのである。それが、下の写真である。レンズを固定している辺りをよく見てもらいたい。不思議な
虹模様と十字の模様が見えるはずだ。
 |
プラスチック等は製造過程での不均一な応力や、外力により複屈折性を示す。光弾性と呼ばれる現象である。そのため、偏光面を直行させた偏光フィルターの間にそういうプラスチックなどを挟みこむと、その弾性体の内部に働いている応力分布の状態を調べることができる。それを応用したのが、偏光顕微鏡などである。
例えば、下の写真はカセットテープのケースの左側部分を、偏光面を直交させた二枚の偏光フィルターで挟んでみたものである。見事に弾性体の内部に働いている応力分布が可視化できているのがわかると思う。これを応用すれば、例えば熱変形をしているようなものであれば、透明体の熱分布も簡易的に見て取ることができる。
 |
そういうわけで、先の写真あるいはそれを拡大した次の写真のように普通では見えない透明なプラスチックレンズの中に隠れている「ストレス」を見て取ることができるわけだ。
 |  |
とりとめもないが、今回は透明なメガネの影に隠れたストレスに光を当ててみた。ちゃんと見ようと思いさえすれば、目に見えるものは数多くある。「見える?見えない?」の境界線はその人自身が決めるのである。「できるかな?」では、これからも色々な「見える?見えない?」を追求し、「見えるかな?」について考えていきたいと思う。
2000-05-27[n年前へ]
■ささやかだけれど、役にたつこと 
メール紹介の小ネタ集
「できるかな?」の話題に関して色々と面白いメールを頂くことがある。その中には、私の知らない色々な面白いことが書いてあるものも多い。今回はそういったものの一部から小ネタ集(探偵ナイトスクープの桂小枝風)をやってみたい。メールは多少こちらで書き換えている部分もあるが、基本的には頂いたそのままである。
まずは、
の時のように計算間違いをしたりすると、さまざまな正解がメールで送られてくる。非常にありがたいことである。簡潔に間違いの個所を指摘してあるメールもあれば、私と同じように迷路にはまり込んでしまった答えが書いてあるメールもある。どちらにしても、私にはとても面白く、ありがたいものである。 例えば、最近で言うとこんな面白い「間違い指摘メール」を頂いた。
早速ではありますがにてどんぐりころころ、どんぐりこと記述されておりますが「どんぐりこ」ではなくて「どんぶりこ」が正しい歌詞だと記憶しております。真偽を確認の後、然るべき行動を取られることを切に願います。 |
「えっ」、と一瞬思うが、口ずさんで、後の歌詞のつながりを考えてみると、確かにそうかもしれない。どんぐりがお池にはまるなら、確かに「どんぶりこ」の方が自然である。桃太郎の桃が「どんぶりこ」と川を流れてきたように、どんぐりも「どんぶりこ」となるのが自然である。
そこで、WEB上で情報を探してみると、
- どんぐりの歌( http://www.jstudy.ne.jp/~donnguri/html/dongurisong.htm )
そして、同じ「どんぐりころころ」ネタと言えば、こんなものもある。
| にて、 - 「どんぐりころころ」と水戸黄門の主題歌の輪唱 - というものを書かれておりましたが、「赤とんぼ」と水戸黄門の主題歌(あぁ、人生に涙あり)も輪唱可能 です。 他に思いついたのが、 おたまじゃくしは、カエルの子。ナマズの孫ではないわいなぁ。も、「あぁ人生に涙あり」の節でいけそうです。 どうも、山田耕作系の曲は合うようですね。以前、「山田耕作の曲は日本語の音韻律に合わせてある。」という話を聞きましたがこれが関係しているのでしょうか? 他に、昔TVで見たものですが、
|
私には水戸黄門の主題歌の題名が「あぁ人生に涙あり」であると知れただけでも、うれしくてたまらない。いいタイトルだ。日本人の心にグッとくるタイトルである。
そして、その後の
- 山田耕作系の曲と「あぁ人生に涙あり」のカノンについての関係性
と、思いつつなかなか手をつけられないでいるので、今回ここに紹介してみた。もちろん、いつか挑戦しようという気持ちは変わっていない。いつか、必ず登場させるだろう。
そして、同じ「モナ・リザ」つながりでは、こういう面白い話を教えてくれるメールもある。
| の福田繁雄氏とモナリザの微笑みで思い出したのですが、トーストの焦げ目で描いた作品を見た記憶があります(これが福田氏の作品だったかどうかあいまいなのですが)。この時の作品は、焼け具合の違うトーストを並べてありましたが、展示が終わった後はどうしてしまったのでしょうか。 インドあたりでやってる砂で描いたマンダラに通じるものがあると思いました。(その場限りのものという意味で…) |
このメールを読んでから、「モナリザ」の自己相似形ソフト 料理材料編 に必ず挑戦したいと考えているのである。そのために写真満載の料理ブックも購入してしまった程である。
他にも色々な知識と言えば、こんな情報もとても勉強になった。
で、ところで、ドレミファソラシドの語源はどこにあるのだろう?SoundOfMusicがdoeの歌のイメージから"doa dear ..."と鼻歌を歌うことはあるが、語源は一体?次の宿題にしたいと思う。とありますが、これはなんと、ドレミ....も歌からとられたもので、<聖ヨハネ賛歌>という歌の歌詞から引用したものだそうです。聖ヨハネ賛歌は当時使われていた、6音音階の各音を正しく理解、視唱させるために各行の開始音が6音音階の各音になっていた曲です。 つまり、聖ヨハネ賛歌の各行のはじめの歌詞が、Ut,Re,Mi,Fa,Sol,Laだったので す。 Do Re Mi、は、もとはフランス語のUt Re Mi Fa Sol La Si Utでしたが、16世紀になってイタリアで呼びにくいUtが現在のDoに変わったのでした。 |
こういう言葉が変化していく様子というのは私のとても興味のあるところである。そういう話、「蝸牛考」、あるいは探偵ナイトスクープの「アホとバカの境界線」のような面白い話があったら、ぜひ私まで教えてもらえるとうれしい限りである。
さて、最後にこんなメールをご紹介したい。これは、さまざまな色空間の多様性について書いたものについて頂いた意見の一部である。
| 複数種類の蛍光色素を用いて動物組織を染色し顕微鏡観察した画像をコンピュータで解析する技術が一般的になっています。ここで使われている疑似カラーが緑と赤ですが、私は緑と紫にしました。2色が重なるところは白くなります。通常使用される疑似カラーで赤を暗く感じることも問題ですが、もっと問題なのは、赤と緑の重なったところを黄色に表示した場合、緑と黄色が区別できないのです。 自分が赤の変わりに紫を使って、緑と紫、重なったことろが白としたのは、これであれば健常者の人でも赤緑色盲の人でも余容易に区別がつくと思ったからです。色盲の人は日本で5%ですがアメリカではその倍以上います。学会の会場や雑誌の読者の中にこのプレゼンテーションが理解できない人が10ー20%いたら、発表している人にも損が生じます。 |
この考えには私もずいぶんと影響を受けた。そのせいで
つくった自作ソフトの色はその方式に合わせたし、では他のソフトの画面をWEB上では色調変換して表示している。 |  |
こういう「ささやか」なやり方ではあるが、私は緑-紫の疑似カラーの布教活動に勤めているのである。
今回は五通のメールを紹介してみた。その他にもたくさんの「面白いメール」を頂いている。別に技術的な話でもなんでもなくて、単に「こんな面白いことがあった」というメールを頂くこともあるが、それもまたとても私には役に立つのである。例え、現実的には「役立たなく」ても、それはとても「役に立つ」のである。
そんな「ささやかだけれど、役にたつこと」を今回はいくつか紹介してみた。そういうことは「どんなことでも」、こちら(jun@hirax.net )まで送ってもらえると、とてもうれしい。