1999-12-16[n年前へ]
■スキー場の特殊相対性理論 
ジャンプの飛距離は何メートルだ?
突然ではあるが、HIRAX.NETのドメインレコードを調べてみると、
Record created on 16-Dec-1998.となっている。自分のドメインのレコードをわざわざ調べたのは、一体いつ取得したのか私自身が忘れてしまったからである。何しろ、「できるかな?」は当初異なる場所での二本立てで公開していたため、私の記憶がごっちゃになっているのである。あと各回の公開順序も実はかなりシャッフルされている。そのため、完全に忘れていたのである。
「できるかな?」はHIRAX.NETのコンテンツの一部である。しかし、HIRAX.NETの誕生日よりも、「できるかな?」の誕生日の方が実は早い。
で書いたように、「できるかな?」はすでに満一年を迎えていたわけである。そしてやっと、本日でHIRAX.NETも満一歳になったわけだ。何はともあれ、目出度いことである。子供の頃やらされた「ドリル」でも3日も続かなかったのに、1年続くとは、正に奇跡である。奇跡はそうそう続かないような気もするが... さて、関係ない話はここまでである。今回の舞台は万座温泉だ。なぜなら、先週末私は万座温泉でスキーをしていたからだ。何故だか理不尽な話しではあるが、私は万座温泉でローレンツ収縮を考える羽目になったのだ。もう少し正確に言えば、スキー場で特殊相対性理論を考える羽目になったのである。(先に断っておくが、私はトンデモ話をマジメな顔で言うことが多い。)
 |
話の発端はスキーに行く前に遡る。職場の今年の新入社員であるタカノリ君(仮名)とスキーの話をしていた。彼は秋田出身であり、子供の頃からスキー三昧の生活をしていた。大学に入り京都へ行ってからは、スキーをやる頻度は下がったが、チョコチョコ行ってはいたという。
そのタカノリ君(仮名)と話していると、彼はさりげなくこう言った。
「10m位のジャンプはよくするスよ。」10mである。2mの身長の人の5人分である。それは、スゴイ。
「えぇ、本当かぁ〜〜」
「いやぁ、そんなのよくやることじゃないスか?」
今回のスキー&温泉旅行は職場(と何故か競合他社)の人達30人程で行った。ほとんどの人は、割にスキーは好きな人が多い。従って、スキーも上手い人が多い。その人達に囲まれながら、タカノリ君(仮名)は断言した。
「6,7mは簡単だけど、10mってスゴイなぁ。」タカノリ君(仮名)、ただ者ではない。
「本当かぁ〜〜」
「えっ、だってただ飛ぶだけじゃないっスか。」
そこで、スキー場でその確認をしたわけである。場所は万座プリンスゲレンデの下部である。リフトとコースが交差する辺りに、ジャンプできる場所があったのだ。そこで、彼は軽く滑り出し、力一杯ジャンプした。
果たして、タカノリ君(仮名)は何メーター飛んだのであろうか? それとも、ただのホラ吹き男爵であったのだろうか?
ところが、その答えをすぐに書くわけにはいかないのである。なぜなら、タカノリ君(仮名)がジャンプをしてみせた時に事件は起こったのである。
「どうスか!10mはいったんじゃないスか!」
「3,4mしかいってねーぞ!おイ!」
これは、一体どうしたことだろうか? しかも、会話はまだ続くのである。
「何でっスか!軽く1秒は宙に浮いてたっスよ!」ますます不思議なことに、時間感覚すら違っているのである。一体何が起こっているのだろうか?
「そんなことはねぇぞ!コンマ数秒だろう!」
私はここで気づいたのである。観測者の間で時間と空間の不一致が生じているのであれば、ここはもちろんアレの登場である。アレと言えば言うまでもない、もちろん特殊相対性理論である。
そう、万座温泉スキー場ではローレンツ収縮を実感することができるのである。「スキー場でジャンプする」という現象を考える際には、「スキー場におけるhiraxの特殊相対性理論」を導入しなければならないのであった。
それでは、簡単に「スキー場におけるhiraxの特殊相対性理論」を説明しよう。今回、生じている不思議な現象は以下のようになる。
登場人物
- タカノリ君(仮名) 速度vでジャンプをしている。
- 観客 静止している。
| タカノリ君(仮名) | 観客 | |
| 飛んだ距離 | 10 | 3 |
| 飛んでた時間 | 1 | 0.3 |
つまり、速度vで飛んでいるタカノリ君(仮名)の感じる空間や時間といったものは、静止している観客に比べて、いずれも3倍程度に膨張しているのである。
通常の世界で生じるローレンツ収縮は、速度vで移動している観測者の空間軸も時間軸も
![]()
倍縮むのであるが(ここでは光速c=1の単位系を使用している)、
であるが、「スキー場におけるhiraxの特殊相対性理論」では、速度vで移動している観測者の空間軸も時間軸も静止している観測者に対して、逆に![]()
倍に延びてしまうのである。もし、ミンコフスキーの時空図を書いて確認しようとする人がいるならば、座標軸の傾きの変化も通常のローレンツ変換と逆に考えてみてもらいたい(その延長で考えていくと、矛盾があるというご指摘メールはノーサンキューである。)。
さて、そもそもローレンツ収縮は、マイケルソン - モーリーの実験結果(エーテルの影響が検出できない)を説明し、なおかつエーテルの存在を認めるために立てられた。それは、「運動体はすべてその運動方向に収縮する」という仮説である。その仮説を理論的に完成させたのが、アインシュタインの特殊相対性理論である(考え方としては根本的に異なるが)。
今回の話の中で「エーテル」に変わるのは、「空気」だろうか? いや、違う。私はむしろ、速度そのものであると、考える。つまり、特殊相対性理論と同じである。スピードを出して飛んでいるという感覚、速度が与える感覚の変化、すなわち速度そのものが、「スキー場におけるhiraxの特殊相対性理論」を要請するのである。
今シーズン、スキー場でせっせとジャンプをする人がいるならば、ぜひ「スキー場におけるhiraxの特殊相対性理論」について考えてみてもらいたい。
このWEBへ来る人の中で、同時期に万座温泉スキー場にいた人はいるだろうか?12/11.12に万座温泉スキー場のプリンスゲレンデの下部でジャンプにいそしんでいたのが、私達の一行である。そして、その中の一人(ショートスキーでせっせと飛び跳ねていたヤツ)はこんなことをずっと考えていたのである。
さて、実際のタカノリ君(仮名)の飛距離がどの程度であるか知りたいと思う人も多いだろう。オマエらの主観的な評価でなくて、実測定した距離を教えろと思う人も多いに違いない。
「絶対的な基準など存在しないから、そんなことは私はわからない。」と言い放ちたいところだが、タカノリ君(仮名)の名誉のために書いておく。彼が飛んだ距離は、2m弱のスキー板で4本分はあった。実は、タカノリ君(仮名)の基準が一番正しかったのである。彼は、「やるときはやる有言実行の人」なのであった。
2000-01-03[n年前へ]
■音場の定位を見てみたい 
立体音感を考える その2
前回(といっても間に他の話も挟まっているのだが)、
で「音の立体感」について考え始めた。今回はその続きである。「音の立体感」を考えるための道具を作る準備をしてみたい。色々なことを考えるには、その目的にあった測定器が必要である。何か新しいことをしようと思ったら、そのための新しい測定器を作成しなければならない(と思うだけだが)。そして、何より私は計測器なんてほとんど持っていない。だからといって、計測器を買うお金があるわけではない。というわけで、困ってしまうのだ。
そこで、立体音感を考えるための測定器を作っていくことにした。といっても、すぐにできるとも思えないので、色々実験をしながらボチボチとやってみることにした。勉強がてら、ボチボチやってみるのである。オーディオ関連のことにはかなり疎いので勉強にはちょうど良いだろう。
資料をいくつか眺めてみたが、特に
- 「立体視の不思議を探る」 井上 弘著 オプトロニクス社
- 音像定位の因子
- 両耳差因子 (音響信号)
- 音の強さ(振幅)の差
- 位相の差
- 周波数スペクトル因子
そこで、いきなりだが今回作成した解析ソフト「音場くん一号」のアルゴリズムは以下のようになる。
- PCのサウンド入力から、サンプリング周波数 22.05kHz、Stereo 各チャンネル8bitで取り込みを行う。
- 取り込んだデータを4096点毎にウィンドウ(Hamming or無し)処理をかける。
- 高速フーリエ変換(FFT)を行う
- FFTの結果の実部について、左右のチャンネルの差分を計算する
次に示すのが、「音場くん(仮名)一号」の動作画面である。「音場くん(仮名)一号」の画面構成は、
- 右側->制御部
- 左側->計測データ表示部
- 音声波形データ(赤=左、緑=右)
- 周波数(横軸)vs左右での音圧の差(縦軸)
- 時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)
 (黒字に赤、緑の色構成は変更の予定) |
計測データ表示部の拡大図を下に示す。
- 音声波形データ(赤=左、緑=右)
- 周波数(横軸)vs左右での音圧の差(縦軸)
- 時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)
この表示計の意味を例を挙げて説明したい。例えば、下の画面では左の方に定位している音が鳴ったときの状態を示している。一番上の音声波形データでは緑(右)の波形は小さいのに対して、赤(左)の大きな波形が見えている。
また、真ん中の「周波数(横軸)vs左右での音圧の差(縦軸)」では横軸100(任意単位)程度の高さの辺りで左チャンネルに位置する音が発生しているのがわかる。
また、一番下の「時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)」では時間的に一番最後(横軸で右側)の方の横軸560、縦軸100位の位置に白い(すなわち左チャンネルに定位する)音が発生しているのがわかると思う。
 |
この曲のイントロでは、「ポンッ」という音が高さを変えつつ、左右にパンニング(定位位置を変化させること)する。
一番下の「時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)」を示したグラフ中で白・黄色(左に定位)と青・黒(右に定位)する音が時間的にずれながら現れているのが判ると思う。
このようにして、この「音場くん(仮名)一号」では音の定位状態についての「極めて大雑把な」計測が可能である(保証はしないけど)。「音場くん(仮名)一号」を使った他の例を示してみる。
下は種ともこの「O・HA・YO」の中から「The Morning Dew」のイントロ部を示したものだ。
- 左(白・黄)チャンネル方向に定位するピアノ
- 右(黒・青)チャンネル方向に定位するガットギター
 |
これはまるでオルゴールのピンを見ているようだ。あるいは、シーケンサーや昔の自動演奏ピアノのロール譜のようである。対位法などの効果をこれで確認したくなってしまう。
さて、ここまでの例は楽器も少なく、比較的自然な定位状態であった。しかし、以下に示すような場合には不自然なくらいの「音の壁」状態の場合である。かなり状態が異なる場合だ。
 |
これは、種ともこの「O・HA・YO」の中から「KI・REI」のラストのラストコーラス部を示したものである。人のコーラスが重なり合っていく部分である。色々な高さの声が重なり合っていく様子がわかるだろう。
ところが、このグラフをよくみると、同じ音が時間的に持続しているにも関わらず、時間毎に定位位置が左右で入れ替わっているのがわかる。
これはきっとエフェクターで言うところのコーラスなどをかけたせいだろう(素人判断だけど)。人工的にフィルタ処理をしているためにこのようになるのだろう。こういう結果を見ると、「音場くん(仮名)一号」をプログレ系の音の壁を解析してみたくなる。
さて今回は、音声の定位状態を解析する「音場くん(仮名)一号」を作成し、いくつかの音楽に対して使ってみた。まだまだ「音場くん(仮名)一号」は作成途中である。これから続く立体音感シリーズとともに「音場くん(仮名)」も成長していく予定である。
さて、一番先の画面中に"Re"という選択肢があるのがわかると思う。もちろん、これと対になるのは"Im"である。FFTをかけた結果の"実部"と"虚部"である。"実部"の方が左右の耳の間での音の大きさの違いを示すのに対して、"虚部"の方は左右の耳の間での位相差を示すものだ。つまり、ある周波数の音が左右の耳の間でどのような位相差を示すものか、測定しようとするものである。
左右の耳に対する音の位相差というものは、立体音感を考える上では避けては通れないのだろう。しかし、位相差を処理しようとすると、どうしたらいいものかかなり迷う部分がある。また、今回のようなFFT処理をかけたときに得られる位相を用いて良いものかどうかもよくわからない。というわけで、今回は位相解析処理は後回し、ということにした。
2000-01-08[n年前へ]
■着メロの音響工学 
この着信音は誰のだ!? 立体音感その3
街中で携帯電話の着信音が鳴ると、周辺の人が一斉に自分のポケットを探る光景というのはよく見掛ける。それは、まるで「クイズ・ドレミファドン」のようである。そう「超・イントロクイズ」そのものなのだ。「このイントロはオレのか!?それとも!?」と皆が考えている瞬間である。
着メロのイントロが始まるや否や、腰の携帯電話に手をやる様子は「おまえは荒野のガンマンか!」とツッコみたくなる程である。
特に、私の勤務先などでは全員が同じPHSを持ち歩いているせいか、着信音が聞こえ始めると、みな自分のポケットを探り始める。もちろん、そのPHSの着信音は数種類ある。しかし、1500人程度の従業員がいるわけだから、1500人/ 数種類だけ同じ着信音があるわけだ。仮に15種類あるとしても、
1500(人) / 15(種類数) = 100(人/種類)つまり、自分と全く同じ着信音のPHSを持つ人が100人もいるのだ。世の中には「自分と同じ顔の人が七人いる」というが、職場に同じ着信音の人が100人もいるのである。これでは、着信音が鳴ると同時に多くの人がポケットを探るのも自然だろう。
もちろん、この解決策として、「着信音でなくてバイブレーターを使う」というものがあるわけだが、何故かその解決策は許されないらしい。不思議である。
さて、そもそも、何故自分の着信音を区別できないのだろうか? まず、その辺りから考えてみることにする。
着信音が鳴ったときに、「自分の着信音かどうか判断するための基準」は二つあるだろう。それは、
- 着信音の種類
- 着信音が鳴っている位置
着信音の鳴っている位置 = 自分の携帯電話の位置が成立するかどうか即座に判断できれば、着信音が同じでも「自分の着信音であるか」の判断が可能ということだ。
つまりは、「携帯電話の着信音という音源の定位」という問題を考えれば良いことになる。もし、「着信音の定位」が判れば、自分の携帯電話の着信音か他の人の着信音かどうかなんてことは考えなくて済むのだ。そう、今回は「立体音感」シリーズその3だったのである。
それでは、一体「着信音がどこで鳴っているのか、すなわち、着信音の定位」が判るためには何が必要なのだろうか?
前回、
で「音の立体感に関する因子」について- 音像定位の因子
- 両耳差因子 (音響信号)
- 音の強さ(振幅)の差
- 位相の差
- 周波数スペクトル因子
周波数スペクトル因子というのは、例えば、
の中の記述指を前方で鳴らしてみて下さい。 そしてすこしずつ手を頭の側方に、手と頭の距離を変えないようにして、移動してみて下さい。 音量がわずかに大きくなったこととある特定の中域および広域の音がより強調されることに気が付かれるでしょう。 この実験では、指を鳴らす動作は一定の音量と周波数を発生する音源として用いられたわけです。 耳は同一の音源が前方から来る場合と、側方から来る場合で全く違う音と聞き分け、頭脳にそれを登録します。 側方の音は若干大きく、また耳たぶのせいで高い周波数で聞こえます。にあるようなものである。
音波が人間の頭部を通過してくる間に音波の周波数分布が変化し、その変化具合で音波がやってきた方向を知ることができるというものだ(多分)。もちろん、位相分布も変化するだろうが、ここでは周波数分布しか考えない。
こういう音像定位の因子における「周波数スペクトル因子」を考える時に、もし音源の周波数スペクトルがごく狭いものだったらどうだろうか?つまり、単一の周波数しか含まない音源だったらどうだろうか?周波数スペクトルが変化するといっても、単一のスペクトルしか含んでいないのだから、振幅が変化する効果しかない。周波数スペクトルの分布は何ら変化しない。
ということは、「音像定位の因子における周波数スペクトル因子」が上手く作用しないことになってしまう。(もちろん、実際には非線形な効果が存在するだろうから、多少は周波数スペクトルも変化するとは思うが。)
これと全く同じことはまたしても「物理の散歩道」で触れられている。ロゲルギスト著の岩波新書「第四物理の散歩道」の「不規則なものの効用 三節」である。純音より不規則な音の方が「立体感」を得られるだろう、と書いている。
今回、「携帯電話の着信音の定位」を「着信音のスペクトル分布」という観点から調べてみることにする。携帯電話の着信音がどのような波形であるか、どのような周波数分布を持っているかを調べるのである。果たして、携帯電話の着信音の周波数分布はどうなっているのだろうか?(部品点数を考えれば、ほぼSin波か矩形波なのが当然だろうが...)
まずは手持ちの機種で着信音の波形とスペクトルを見てみることにした。使った機種を以下に示す。
 |
それでは、着信音No4と着メロ「この木何の木」の波形とスペクトログラムを次に示す。それぞれのグラフ中で上は「時間vs周波数分布」を示すスペクトログラムであり、下は「時間vs強度」の波形グラフである。
まずこれが、着信音No.4の波形とスペクトログラムであり、
 |
こちらが、「この木何の木」の波形とスペクトログラムだ。
 |
どちらも周波数分布はそれほどブロードではない。すると、「音像定位の因子における周波数スペクトル因子」を用いた「立体音感」がうまく働かないかもしれない。ただし、着信音No.4に関しては時間的に変化しないが、着メロ「この木何の木」に関しては、当然だが時間的に変化していく。
この違いが果たして、「着信音の音像の定位」の判断を左右するものか、自分の耳で実験することにした。着信音No.4と着メロ「この木何の木」を鳴らした時に、どこから鳴っているように聞こえるか判断してみるのだ。
目をつぶり頭の周囲で着信音を鳴らし、その定位を判断してみた。すると、色々な着信音を聞いてみたがいずれも定位の判断がしづらかった。特に頭の前後の判断がしづらい。それは、着信音No.4と着メロ「この木何の木」でも同様であった。やはり、純音に近いと「音像定位の因子における周波数スペクトル因子」が働きづらいのかもしれない。
そして、着信音No.4と着メロ「この木何の木」だが、むしろ着信音No.4の方が判断をしやすかった。メロディだと音が変わるときに定位が変わるかのような感覚を受けた。そのため、判断をしにくかった。もちろん、これは私だけの感覚かもしれない。その辺りは被験者を増やして実験をしてみたい(再実験をする日が来るかどうかは大いに疑問であるが)。
また、もしかしたら着信音No.4の方が矩形波に近く、純音でないのが良かったのかもしれない。もしかしたら、の話だけれど。
もし、今回使った音を聞いてみたい人がいるならば、
これを聞いてみてもらいたい。ただし、サイズがでかいので要注意だ。あとバックグラウンドがうるさいのはハードディスクとファンの回転音である。困ったものだ。 最近多い「同時発声数が多い着メロ機能」というのも、使って実験すると面白そうだ。しかも、音が分厚いヤツがあると、案外良いモノかもしれないな、とうらやましく思ったりするのである。そして、着信音スピーカーがプアァで歪んでいる機種なんかが、色々な周波数成分を含んでいて、実は「着信音の定位」に関しては良かったりするのかもしれない、と考えたりする。しかし、こちらはチットモうらやましくないのであった。
2000-01-17[n年前へ]
■夜のバットマン 
超音波を可視化しよう
どんなものに対しても、「超」という文字をつけるという安易な手段はよく使われる。「超人ハルク」、「超常現象」、「超能力少年」、「超解像」等々である。「超Ultra」+「人 Man」ならば「超人 Ultra-Man」、すなわち、ウルトラマンだ。こういう風に並べてみると、何かアヤシげなものが多いような気がするが、それは私の気のせいだろう。
「超」をつければ、「モノスゴイ」という印象を受けるかというと、必ずしもそういうわけでもない。最近、「お笑いパソコン日誌」でよく取り上げられているBTRON仕様OS「超漢字」などは、その最たるものである。個人的には好きなネーミングなのだが、その名前を聞くと昔の「超兄貴」というゲームを思い出してしまうのだ。筋肉ムキムキなマッスルな兄貴達が動き回るゲームが思い出されるのだ。そして、そんなマッスルなデスクトップのイメージが連想されてしまうのである。困ったものである。
「超」の発音は同じ日本人でも一定というわけではない。あまりものを考えないタイプの人の場合、「超」でなくて「チョー」という発音するらしい。その使用例が、「チョー、ムカツクー」などである。これらの人を「チョー人」と呼ぶべきである(既に誰かが言っていそうな気がするが...)。
何故、こんな話になるのだ。話がずれた。
本題である。今回遊んでみるのは「超 Ultra」+「音波 Sonic」=「超音波UltraSonic」である。色々な応用はあると思うが、まずは基礎から始めたい。そういった場合、色々やり方はあるのだろうが、まずは実感するのが「できるかな?」のやり方である。そこで、まずは超音波を実際に聞いてみることにした。
普通は聞こえない周波数の音波を超音波というわけであるから、超音波を聞くというのは何ともスリリングである。参考までに、色々な動物の可聴域を以下に示す。
人間は大抵20kHz前後が上限であり、コオロギと同じくらいである。超音波と言えば、コウモリであり、コウモリは200kHz弱位が上限のようである。
 |
まずは、超音波を聴くための情報を探してみた。すると、何とも素晴らしいサイトがあった。
- がーさんとたぬさんのホームページ( http://www.seaple.icc.ne.jp/~mixseeds/ )
また、コウモリ探知器である。バットディテクターに関しては、
- Bat Detecter ( http://www3.justnet.ne.jp/~hhas/BD.HTM)
迷わず、先の「がーさんとたぬさんのホームページ」の「釜利谷東ミックスシーズ」から、バットディテクターを購入することにした。こういう楽しいオモチャはすぐに手に入れるに限る。これが、購入したバットディテクターである。
 |
このバットディテクターは超音波マイクからの入力を40kHz程度の周波数の信号と合成するものである。そして、その結果得られるビート音、うなり音を耳で聞くものである。
わからない人はほとんどいないと思うが、一応書いておく。例えば、10Hz周波数の音があるとしよう。
 |
この波形は細かすぎて、この画面では目に見えないだろう。しかし、この波形と11kHzの周波数の音を合成してみる。
 |
すると、10kHzと11kHzの周波数の差である1Hzのうなりが発生する。この1Hzのビート音の波形は目に見えるだろう。こういう原理である。
しかし、これでは実は説明が不十分であると思うのだが、今回はこれだけの説明で終わらせておくことにする。
さて、どんな超音波を聴くかであるが、「できるかな?」の実験を行うときには、大抵ビールを飲んでいるのである。今日もビールとお好み焼きがそばにある。そこで、お好み焼きを焼く音を
- 可聴域
- 超音波領域
もちろん、私自身は自分の耳で実感しているわけである。しかし、WEBページ上であれば、可視化した方が良いだろう。waveファイルはサイズが大きいし...
 |
途中のスパイク部はお好み焼きをひっくり返した時の音である。レベルを合わせているわけではないし、実験は実に大雑把なものであるが、そんなに真剣に行う実験でもないのでこれで良いことにしておく。
 |
硬いものと何かを擦ると超音波が実に多く発生するが、絨毯みたいな柔らかいもの相手ではあまり超音波が発生しなかったりして実に面白い。衣擦れの音などは実にリアルである。何か色っぽい音ですらあるように感じる。(それは私だけかもしれないが...)
超音波に関してはまだまだ色々とやってみたい実験がある。実は以前秋月で買った超音波マイク・スピーカセットが家に転がっていたりする。これを使って、次回は超音波オモチャを作成してみたいと思う。
さて、今日はTVで「バットマン&ロビン Mr.フリーズの逆襲」を放映するようだ。バットマンの映画は何故か夜の街が舞台である。
バットマンと言えば、Bat(コウモリ)+Man(男) = コウモリ男だ。このTVを見たあとの私はきっとバットマンになりきっているだろう。バットディティターを耳に差せば、私だって堂々たるバットマンだ。
というわけで、バットディテクターを耳に差し若葉マークをつけたバットマンは、夜の街へ出撃するのであった。夜のバットマンは眠らないのである(下品なギャグ禁止)。
2000-01-27[n年前へ]
■「富士の樹海」を目指せ 
磁界を可視化しよう
以前から探していた「面白いもの」を入手した。この写真がその「面白いもの」なのであるが、何だかわかるだろうか? ちなみに、大きさは「1cm×5cm」位のシートである。
 |
これは「マグネビュアー」というものである。磁界を可視化してくれるシートだ。マイラーフィルムの間に磁性体を混入させたマイクロカプセルを入れることで、磁界に対する配向性を持たせたものだ。と、言葉でいってもなかなかわかりにくいので、磁界を可視化した写真を示してみる。何しろ、百聞は一見に如かずである。
次の写真は某ピザ店のマグネットシート(よく冷蔵庫の扉に張り付ける奴)の上に「マグネビュアー」をのせたところである。ピザ屋は私の食生活を支えていると言っても良い。私が生きているのはピザ屋のおかげである。
 |
私の「命の恩人」でもある某ピザ店のマグネットシートがつくる磁界が見て取れるだろう。磁界が可視化されているのである。
本WEBではこれまで様々な「可視化」で遊んできた。例えば、
- 感温液晶でNotePCの発熱分布を可視化する
- ハードディスクのエントロピーは増大するか?- デフラグと突然変異の共通点 - (1999.03.28)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- 恋の力学 -恋の無限摂動 - (1999.12.21)
- WEBサイトの絆 - WEBの世界を可視化しよう- (2000.01.13)
- 夜のバットマン - 超音波を可視化しよう- (2000.01.17)
上に示した「某ピザ店のマグネットシートの表面」の磁界の様子も面白いが、もっと面白いのは「某ピザ店のマグネットシートの境界」の磁界を可視化したものである。
それが下の写真である。磁界の様子が実感できるのではないだろうか?
 |
下に示す図はドーナツ型の磁石の周りの磁界をCUPSを用いてシミュレーション計算した結果である。この計算結果と同じようなものが「マグネビュアー」を使うと簡単に可視化できる。
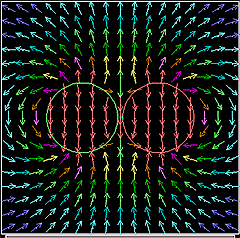 |
普通、こういった磁界の可視化は磁気造影剤や砂鉄みたいな磁性体粒子を用いるのであるが、そういったものはどうにもハンドリング性にかける。液体や粉体などを家の中で実験に使うのはイヤである。いや、もちろん仕事で使うのもイヤであるが... そこで、この「マグネビュアー」が登場するわけだ。
それでは、その他の面白そうな磁界を可視化してみたい。磁界と言えば、やはりアレの登場だろう。もちろん、アレと言えば磁気カードである。クレジットカードや銀行のキャッシュカードといった磁気カードだ。一例を次に示してみる。こんなヤツだ。
 |
カードの下に黒い磁気データ記録部があるのがわかるだろう。
それでは、その「磁気データ記録部」に「マグネビュアー」をのせてみよう。はたして、磁気データは可視化されるだろうか?
 |
といっても、この写真ではわかりにくいので、「マグネビュアー」を拡大してみよう。すると、バーコードのような模様が見えるのがわかると思う。「磁気データ」が簡単に可視化されているわけである。この「マグネビュアー」と普通のスキャナーがあれば磁気データ読み取り機がなくても磁気データが読みとれるのである。
 |
しかし、このカードに関しては内容を解析するとマズイ事情があるので、次回に「ソフマップ」のカードを題材にして磁気カードの内容を可視化してみるつもりだ。題して、
- ソフマップでお買い物 - 磁界の可視化とバーコード - (仮称)
さて、話は変わるが、私はこの「マグネビュアー」を手に「富士の樹海」を目指すつもりだ。「富士の樹海」では」方位磁針が変な方向を示すと伝えられている。そしてまた「富士の麓」ではとかく人は判断を誤りやすいとも聞く。船頭多くして船山に登ると言うが、「富士の樹海」には判断を誤った船が沈没しまくりである。
私は「富士の樹海」の真実をこの「マグネビュアー」で明らかにするつもりだ。「富士の樹海」の謎を明らかにするのである。何故、方位がそして人が判断を誤るのか、その謎を明らかにするのだ。
しかし、もしも、もしも、の話であるが、本WEBの更新が止まった際には、「富士の樹海」で私が眠っていると思って欲しい。「マグネビュアー」が役に立たないはずがないのだが、きっと何か判断を間違えたのであろう。そうそう、あくまで「富士の樹海」である。「富士の裾野」ではないので念のため...