hirax.net::Keywords::「少年」のブログ

■春夏秋冬　

　東京駅、美少年に行くがいっぱい。で、危うく八重洲口難民になりかけるが、駅ビルの中の「どんなときも、どんなときも」入れる（はいれる、でなくて、いれる、と読むのが正しい）あの店で飲む。
　やっぱり、とても、さみしいな。

■菊姫　

　年初から上野駅で飲んで、さらに東京駅美少年で飲む。いつものように、とりあえず飲んで銘柄を当てる利き酒セットを頼み、初めて当たった。偶然か、これまでの投資のおかげか？今回は「美少年」「銀盤」「???」で、謎のお酒「???」は「真澄」で大当たり〜。当たった景品？として「菊姫」をもらう。で、気づくと、テーブルの上には升酒・コップ酒がたくさん…。（リンク）

■究極の選択 テキスト編　

　いつものように自分の英語スキルの無さを実感して、英語の本を読もう、と決めたのです。が、文字の多いものは読めるとも思えないので（自分をよく知っているのだ）、マンガに決めました。が、空港の本屋にあったのは「金田一少年の事件簿」と「部長 島耕作」の二種類だけだったので、しょうがなくストーリーを楽しめそうなモノ、ということでいつもなら絶対に読まない「盗作マンガ」を買いました。はい、「金田一少年の事件簿」を買ったのです。
　で、これを読んでいたとき、ふと私は思いました。これ読んで覚えたフレーズとか単語って一体いつ役に立つんだろう？って思ったのです。
　私が、周りでやたら殺人事件が起きたり、嵐の山荘に取り残されたりする高校生なら、そんな単語やフレーズを使うシチュエーションは沢山あると思うのです。
　でも、残念なことにそんなシチュエーションには私は陥ったことがありません。いえいえ、私どころがほとんどの人はそんなシチュエーションには陥らないと思うのです。これからも、そして未来も。だって、周りでやたら殺人事件が起きる高校生なんてものすごく非現実的な設定です。「死体消失トリック」とか「犯人はオマエだ！」とかいうフレーズを覚えても、きっと何の役にも立たないと思ったのです。
　そこで、私はさらに思いました。じゃぁ、私は「部長 島耕作」を選べば良かったのでしょうか？島耕作のようなシチュエーションなら起こりうるのでしょうか？いえいえ、それも絶対に違います。何事にも女性と「良い関係」になり、すべてのピンチをオンナで切り抜けていく出世人生なんて、そうそうないと思うのです。少なくとも、私にそんな状況が訪れるとは思えません。全てを暴力と土下座で切り抜けるサラリーマン金太郎もたいがいですが、全てをオンナで切り抜ける島耕作もひどすぎる設定です。世の中にはこの二種類のサラリーマンしかいないのでしょうか？いいえ、そんなことは無いハズです。何事も切り抜ける道が「暴力・オンナ・土下座」でしか切り抜けられないなんて、それではサラリーマンというよりヤクザ屋さんです。いや、もしかしたら、サラリーマンもヤクザの一種なのかもしれませんが、私はヤクザ屋さんを目指すにはちょっとばかり弱すぎます。
　あるいは、島耕作を見習えば、もしかしたらピローロークが上手になるかもしれませんが、それは私の意図するところではありません。それに、島耕作のピローロークが上手いとも私には思えません。私には何で島耕作がモテるのか全然理解できません。あっ、そんなことは関係ないですね。
　で、私は思ってしまったのです。殺人事件に囲まれる高校生とかオンナに囲まれる島耕作とか、ありえない設定のマンガは果たして語学力向上の役に立つのか？と。つまりは、出版社の講談社に「オマエはホントに読者の語学力向上を考えているのか」と小一時間問いつめたくなったのです。どうせなら、「某理系ミステリー」とか「動物のお医者さん」とか辺りをお願いしたいのです、ハイ。

■映画のフィルムを並べたスクラップ　

映画大好きの「元」少年少女達へ

　先日、「お笑いパソコン日誌」で3次元画像ブラウザ「みょう絵」というものを知った。画像ファイルを日付や色の特徴などで三次元空間に並べてみる、というソフトだ。下の図がその「みょう絵」の動作画面だけれど、こんな風に三次元空間に配置された画像が散らばる中を「みゅぃーん」と動く感覚が結構気持ち良い。
 

「みょう絵」

　で、その「みょう絵」をいじって

　欲を言えば画像だけでなくて、色んな文章や音楽や気持ちとか、世の中のありとあらゆるものをこんな風にして眺めてみたいなぁ、と思った。あのころ撮影した写真や、眺めた景色や、読んだWEBサイトや…、とにかくありとあらゆるものを。

　余談ですが、Windows XP はムービーファイルをサムネイル化してくれるんですが、あらゆるファイルをそうしてくれればいいのにと思ったり。

　映画が展開していくそのストーリーの時系列と、その中の色々な各舞台を三次元的に眺めてみたいと思ったのだ。そして、さらにはその映画の世界の中を三次元的に散策してみたいと思ったのである。

　もちろん、それは映画の動画ファイルを静止画に展開して、それを「みょう絵」で開けばよいだけの話である。以前、動画ファイルを静止画に展開するアプリケーションを作ったこともある。

　とはいえ、それを使って映画をキャプチャーしたファイルをそのまま静止画に展開するわけにはいかない。そんなことをしたら、ものスゴイ数の静止画ができてしまうからだ。1秒あたり約30枚もの静止画を含む動画をそのまま静止画に全部落としたら、一体どれだけのファイルができるだろうか？たった2分位の映画の予告編だって、展開したら何と3600枚である…。これだけの画像を読みこませたら、少なくとも私の遅いPCでは「みょう絵」がストライキを起こすことは確実だ。

　そこで、映画の動画ファイルの中から、場面が変わるごとに一枚づつ静止画を抽出してみることにした。そうすれば、映画の中の色々な場面をそれぞれ一枚づつの画像として眺めることができる。そして、その画像を集めれば、その映画の色々な場面を一枚のノートにして見ることができるわけである。

　というわけで、作ってみたのがこのAVI2Stillsである。いつものように、テキトーに仕立て上げただけだ。下の図がAVI2Stillsの動作画面である。ちなみに、この画面中で、TrigerLebelは場面変化を検出する感度を示すパラメータで、多分60位が適当だと思う。そして、SkipFrameは動画ファイルの中を何フレーム毎に調べていくかを示すパラメータである。展開スピードが気にならなければ1でも構わない。

• avi2stills.lzh 497kB

AVI2Stillsの動作画面

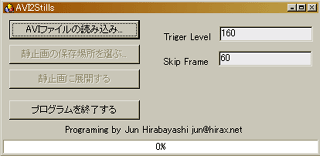　このソフトができたところで、試しに - ロケット制作に憧れる少年達を描いた「遠い空の向こうに」"OctoberSky"( = 原作 "Rocket Boys"のアナグラム) - の中の各場面を抽出してみたのが下のスクラップである。予告編の中の各シーンが絵コンテのように抽出され、並べられていることが判ると思う。
 

October Sky ( 遠い空の向こうに )

　こんな風に自分の好きな映画の場面を全部テキトーに抽出して、あとは「みょう絵」で眺めてみれば、その映画の世界を三次元的に散歩できるのである。というわけで、北村薫原作の映画「ターン」の予告編の世界を「みょう絵」で眺めてみたのが下の図である。
 

「みょう絵」で眺める「ターン」の世界

　静止画では判りにくいけれど、立体的に配置された「映画空間」の中を散策してみるのは、やはりちょっと面白い。これで、欲を言えば各場面に近づくとその場面で流れていた音楽やセリフが聞こえてきたら、面白いと思う。それは、ムソルグスキーの「展覧会の絵」のようで気持ちが良いはずだ。そして、そうすれば気持ちが良いだけではなくて、今の「みょう絵」に足りない「画像だけではない何かをも眺めること」ができるわけだ。
 

　またせっかくだから、「みょう絵」で眺めて終わりにするのも少しもったいないので、以前作った写真アルバム風のスクリーンセーバー"FilmStrip99"(手元のWindows2000では手直しが必要みたいだが…)で、白黒写真のコンタクトフィルム風のスクリーンセーバーを動かしてみた。それが下の画像である。映画のフィルムでなくて、写真のフィルム風だというところはご愛敬で許して欲しい。ちなみに、下の一連の画像は"SomeoneLike You"「恋する遺伝子」の予告編から変換したものである。

　こんな風に自分の好きな映画の予告編などを使って自分用のスクリーンセーバーを作ってみるのも面白いと思う。今なら、たくさんの映画の予告編にオンラインでアクセスできるし、その予告編の動画ファイルがもしmov形式ならmov2aviを使って、それがもしrealvideo形式ならTinraを使えば、AVIファイルに変換できる。そして、今回のAVI2Stillsを使えば良いだけなのである。
 

Someone Like You ( 恋する遺伝子 )

　ところで、こんな切り取った映画のフィルムを繋いだ一連のシーンといえば、ニューシネマパラダイスのラストシーンを思い出す。アルフレードの遺品、「主人公が覗き見ていた一連の場面」を繋いだシーンのフィルム、に主人公が涙したように、かつて少年少女だった映画大好きの人達がそれぞれ自分用のそんなスクラップフィルムを作ってみるのも面白いかも、と思う。そして、ふと思うことがあった時に眺めてみるのも、趣があるかも。

■「やおい」の評価演算子　

ベクトルの彼方で待ってて II

　東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか？

「福田Ｘ小泉っていうのは、結構上手くやっているのかな？」

「あれは、福田Ｘ小泉じゃなくて、絶対あれは小泉Ｘ福田なのー」

「福田Ｘ小泉と小泉Ｘ福田は全然意味が違うのー」

「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」

• やおい　→　一部の女性が好む「男性同士の恋愛もののストーリー」のこと
• Ｘ　→　やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…

　で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。　今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。

　で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
 

　まずは、色々な人物（実際の人物であったり、小説などの登場人物であったり）のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を

1. 攻めベクトル
2. 受けベクトル

SM平面上のサドくんとMくん

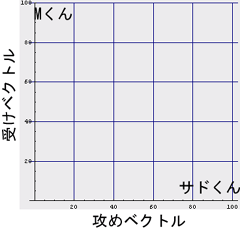　そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、

カップリング適性ベクトル = （攻め度(s)、受け度(m)）

A×Bのカップリング適性 = ( As * Bm - Am * Bs )
　　　　　　　　　　　　　　　 = Aさんの攻め度 * Bさんの受け度
　　　　　　　　　　　　　　　　　　- Aさんの受け度 * Bさんの攻め度

　とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか（?）「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。

　ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。

　これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。

　一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。

　「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
 

　そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
 

「愛はどんな形をしているか知っているか？」

「見た事ないからわかりません。」

「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう？... 異性愛か、同性愛か、そんなものじゃない　　…たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」