hirax.net::Keywords::「視界」のブログ

■「鳥の群れ」と「資本主義」　

　株価の乱高下に関するニュースがメディア上に溢れている。

　資本主義はなぜ不安定なのだろうか。それは基本的に投機によって成立しているからだ。
　岩井克人

　Boidsは大きく分ければ２つのルールで動く。「近くのものから少し離れる」・「けれど、周りの集団に動きを合わせ・その集団に近づこうとする」というルールで動く。投機を動かす鳥たちも、何か経済の言葉で翻訳してみれば、きっとそんなルールで動いているのだろう。

　どの馬券を買えばいいかわからない？
ほなら、一番人気を買っておけばええやろ。
俺は違うけどな。
競馬を見に行った時の友人の言葉

　競馬を成り立たせているのは、意見の違いだ。
マーク・トウェーン

■「視界の幅」と「視点をずらす」　

　森達也の「視点をずらす思考術 」の「付けたしのエピローグ」より

　世界は広い。でも人の感覚の幅はとても狭い。さらに可視光線の幅は電磁波全体のほんの一部でしかない。つまり、見える光と見えない光がある。認知できる音波の幅もとても短い。聞こえる音と聞こえない音がある。

　だからもそも可視光線の幅がほんの数ミリずれたなら、それまで見えていなかったものが眼前に現れる。

　だからもずらす。可視光線の幅はコントロールできないけれど、視点くらいはずらすことができる。たったそれだけのことでも、まったく違う世界が眼前に現れる。

■「吹雪中の視界距離の公式」で知る「雪を舞わせる風の怖さ」　

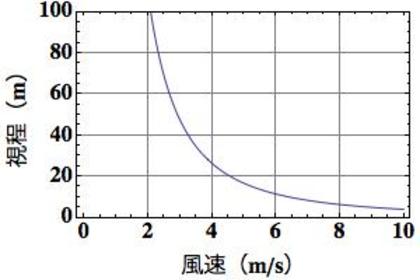　「吹雪中の視界距離の公式」で知る「雪を舞わせる風の怖さ」を書きました。

　上式でとても興味深いのは、視界（視程）が「１立方メートルあたりに存在する雪の重量（飛雪空間密度）」と同じくらい「雪の速度」に影響を受ける、ということです。つまり、たとえば風速（雪を動かす風）が２倍増すと、あたかも目の前を舞う雪の量が２倍増えたのと同じ影響がある、ということになります。

　ここで使った式（関係）は、光学的・視覚的な機構を考えてみると、少し興味深いものに思われます。…といったことは、また明日にでも書いてみることにします。

■続 「吹雪中の視界距離の公式」で知る「雪を舞わせる風の怖さ」　

　「吹雪中の視界距離の公式」で知る「雪を舞わせる風の怖さ」で使った「吹雪中の視界を示す式」は、このようなものでした。
　視程（m）＝10^(-0.886 Log[飛雪空間密度（g/m^3） 速度（m/s）] + 2.648)
この式は、視界（視程）が「１立方メートルあたりに存在する雪の重量（飛雪空間密度）」と同じくらい「雪の速度」に影響を受ける、というものです。 つまり、たとえば風速（雪を動かす風）が２倍増すと、目の前を舞う雪の量が２倍増えたのと同じ程度の影響がある、という式です。

　この式は、単純に解釈しようとすると、少し不思議に感じられる式です。なぜかというと、ごく単純に考えると、風速（雪粒子の相対速度）が増しても視界の程度は変わらないように思えてしまうからです。

　たとえば、冬景色に対して、ほぼ無風下でほんの少しの雪が降っていたとします（下左写真）。雪粒子の量が１０倍に増えた場合の視界を、光の演算や視覚がすべて線形な重ね合わせができるという条件下でシミュレーション計算してみると、下右写真のようになります。確かに視界が悪くなっています。

　

　しかし、同じように今度は、雪の量を１０倍に増やすのではなく雪の速度を１０倍に増やし、（さきほどと同じように）光の演算や視覚がすべて線形な重ね合わせができるという条件下でシミュレーション計算してみると、基準視界（下左写真）は下右写真のようになります。…おや、視界が悪くなるどころか、むしろ「わりと綺麗に景色が見えている」ような結果になっています。

　

　すべての演算に線形性が成り立つとすると（また、風景中に反射率が低いものしかないという条件でない限りは）、「雪粒子の速度が増しても、視界が悪くなるわけではない」という結果になってしまいます。なぜかというと、雪の動きが早くなると、刻々の瞬間に各々の方向に対して雪が景色の「見え」を遮る・白く見せる効果が平均化・均一化され、結果として「視界全面に対して”雪が存在する比率でコントラストを低下させる”」という効果しか生じないからです。

　しかし、それは「現実の吹雪中の視界の程度」を反映していない（冒頭の式とは挙動が違う）ということは、「すべての演算（光演算や視覚）がすべて線形な重ね合わせができる」という前提は「合ってない・間違ってる」のだろう…ということになるわけです。

　風速（雪を動かす風）が２倍増すと、目の前を舞う雪の量が２倍増えたのと同じ程度の影響があるというこの式は、意外に面白い式です。冬の夜長のこの時期、こんなパズルを解いてみるのはいかがでしょうか。

■スケベニンゲン海岸の国際花火大会　

　夜１０時近く、スケベニンゲン（Scheveningen）海岸に行ってみた。「国際花火大会」が開催されていて、波間の向こうで打ち上げられている花火を眺めていると、（夏が始まっていた実感すら未だないのに）もういつの間にか夏が終わっちゃうんだなぁ…と不思議な気持ちになってくる。

　方向的には、この花火の先、海の向こう１５０ｋｍくらい先に、イギリスがあるはずだ。…といっても、地球は丸いから、いくら障害物が無かったとしても４ｋｍくらい先までしか見通すことはできない。

　けれど、今眺めてる場所から１７００ｍくらいの上空まで視点を高く上げてみれば、海の向こうのイギリスが見えるはず。たとえば、地上２０００ｍ近くまで、空高く上昇することができるドローンがあったなら（そして法規制がそれを許すなら）、遙か遠くまで広い視界を見通すことができて…とても心地良いに違いない。