2013-01-08[n年前へ]
■続 「吹雪中の視界距離の公式」で知る「雪を舞わせる風の怖さ」 
 「吹雪中の視界距離の公式」で知る「雪を舞わせる風の怖さ」で使った「吹雪中の視界を示す式」は、このようなものでした。
「吹雪中の視界距離の公式」で知る「雪を舞わせる風の怖さ」で使った「吹雪中の視界を示す式」は、このようなものでした。
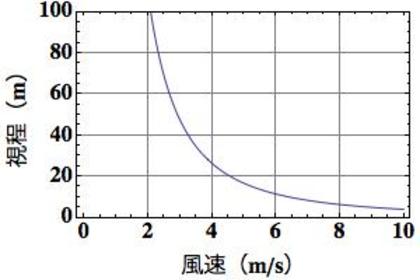
視程(m)=10^(-0.886 Log[飛雪空間密度(g/m^3) 速度(m/s)] + 2.648)
この式は、視界(視程)が「1立方メートルあたりに存在する雪の重量(飛雪空間密度)」と同じくらい「雪の速度」に影響を受ける、というものです。 つまり、たとえば風速(雪を動かす風)が2倍増すと、目の前を舞う雪の量が2倍増えたのと同じ程度の影響がある、という式です。
この式は、単純に解釈しようとすると、少し不思議に感じられる式です。なぜかというと、ごく単純に考えると、風速(雪粒子の相対速度)が増しても視界の程度は変わらないように思えてしまうからです。
たとえば、冬景色に対して、ほぼ無風下でほんの少しの雪が降っていたとします(下左写真)。雪粒子の量が10倍に増えた場合の視界を、光の演算や視覚がすべて線形な重ね合わせができるという条件下でシミュレーション計算してみると、下右写真のようになります。確かに視界が悪くなっています。


しかし、同じように今度は、雪の量を10倍に増やすのではなく雪の速度を10倍に増やし、(さきほどと同じように)光の演算や視覚がすべて線形な重ね合わせができるという条件下でシミュレーション計算してみると、基準視界(下左写真)は下右写真のようになります。…おや、視界が悪くなるどころか、むしろ「わりと綺麗に景色が見えている」ような結果になっています。


すべての演算に線形性が成り立つとすると(また、風景中に反射率が低いものしかないという条件でない限りは)、「雪粒子の速度が増しても、視界が悪くなるわけではない」という結果になってしまいます。なぜかというと、雪の動きが早くなると、刻々の瞬間に各々の方向に対して雪が景色の「見え」を遮る・白く見せる効果が平均化・均一化され、結果として「視界全面に対して”雪が存在する比率でコントラストを低下させる”」という効果しか生じないからです。
 しかし、それは「現実の吹雪中の視界の程度」を反映していない(冒頭の式とは挙動が違う)ということは、「すべての演算(光演算や視覚)がすべて線形な重ね合わせができる」という前提は「合ってない・間違ってる」のだろう…ということになるわけです。
しかし、それは「現実の吹雪中の視界の程度」を反映していない(冒頭の式とは挙動が違う)ということは、「すべての演算(光演算や視覚)がすべて線形な重ね合わせができる」という前提は「合ってない・間違ってる」のだろう…ということになるわけです。
風速(雪を動かす風)が2倍増すと、目の前を舞う雪の量が2倍増えたのと同じ程度の影響があるというこの式は、意外に面白い式です。冬の夜長のこの時期、こんなパズルを解いてみるのはいかがでしょうか。


