1999-03-25[n年前へ]
■電界計算をしてみたい[有限要素法編その1] 
有限と微小のパン
今回のサブタイトルは一目瞭然であるが、森博嗣のミステリのタイトルそのままである。
 |
何故、「電界計算をしてみたい-有限要素法編その1-」が「有限と微小のパン」に繋がるのか。もちろん、"有限要素法"と"有限と微小のパン"の「有限」をかけた駄洒落ではない。有限要素法を考えるとき、私は森博嗣に足を向けては寝ることができない。それが、なぜかは下の本を見ればわかる。
 |
これは、学生時代に有限要素法を勉強するために使った本である。「森 博嗣 著」と書いてあるのがわかるだろうか。いや、まさかこの本の作者がミステリを量産するとは想像もしなかった。ビックリである。講談社ノベルズと森北出版の両方から本を出している人は他にはいそうにない。
本題と関係のない話はここまでにしておく。今回はMathematicaで有限要素法を用いて静電界計算を行いたい。とりあえず、ソルバーとプリ・プロセッサまでつくる。その応用は続きの回で行いたい。Mathematicaで有限要素法を勉強するには、森北出版の依田 潔 著「Mathematicaによる電磁界シミュレーション入門」を参考にした。任意の電荷配置のPoisson方程式を解くようにしてある。
次回に詳しく計算モデルの説明を行うので、今回は計算モデルの詳細については記述しない。Notebook内に、モデルの詳細は記述してある。
このNotebookを使った計算、出力例を以下に示す。
| 平行平板電極の間に誘電体層があるモデル | 平板電極と三角柱電極の間に誘電体層があるモデル | 平板電極と円柱電極の間に誘電体層があるモデル |
 分割要素 |  分割要素 |  分割要素 |
 電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |  電位表示(色がきちんとしたhueでないことに注意) |
 半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |  半分の領域の電位を鳥瞰図にしたもの |
Mathematica3.0のHTML出力は大変便利だが、漢字が化けるのが困りものだ。しかも、ちょっと似た漢字に化けてしまうからわかりにくい。今回のNotebook中で化けた漢字を以下に示す。
- 油界 <- 電界
- 堰素 <- 要素
- 誘油 <- 誘電
- 姦み込む <- 組み込む
- 表傭 <- 表面
- 壓さ <- 高さ
- 堆心 <- 重心
- 肖似 <- 近似
- 内占 <- 内部
- 傭積 <- 面積
- 回寂 <- 回転
- 進当 <- 適当
- 懷瞰 <- 鳥瞰
中国語みたいな化け方である。しかも、意味としても何か変な化け方である。いつか、この対処方法と理由を考えてみたい。それにしても、週末の遊び道具としてはMathematicaは素晴らしいと思う。
1999-09-10[n年前へ]
■「こころ」の中の「どうして?」 
漱石の中の謎とその終焉
考えてみると、www.hirax.netには夏目漱石が時々顔を出す。例えば、
などだ。もともと、夏目漱石は寺田寅彦・ロゲリギストといった物理学者の流れの源と言っても良いものだから、その影響を多々受けている私のWEB中に出てくるのは自然なのだろう。というわけで、今回こそは夏目漱石がメインの話である。漱石の「こころ」を「夏目漱石は温泉がお好き?- 文章構造を可視化するソフトをつくる - (1999.07.14)」「失楽園殺人事件の犯人を探せ- 文章構造可視化ソフトのバグを取れ - (1999.07.22) 」で作成した文章構造可視化ソフトWordFreqで解析してみるのだ。そして、「こころ」で繰り返し問われる謎がどのようにして終焉を迎えていったかを考察してみたい。いや、考察というほどのものではなく、考えてみたい、それだけだ。
何故、私がそういう気持ちになったかといえば、それは小山慶太著の「漱石とあたたかな科学」講談社学術文庫を読んだせいである。
今回のテキストである漱石の「こころ」は
- 青空文庫 ( http://www.aozora.gr.jp/)
言うまでも無いと思うが、「こころ」は学生である「私」と「先生」との間で進む物語である。「私」が先生と出会い、そして「先生」の物語が語られる。
それでは、「先生」と「私」の出現分布を可視化してみる。両者とも1100行辺りで大きく変化しているのがわかる。これは、ここから「下 先生と遺書」に入るからである。一人称である「私」は学生の「私」ではなく、「先生」である「私」になる。ここからは「先生」である「私」の物語になるのである。
また、冒頭をピークとして「先生」の出現頻度は単調に低下していく。学生である「私」から、先生である「私」への視点の移り変わりはもしかしたら冒頭から形作られているのかもしれない。
 |  |
ところで、「こころ」は「どうして」という謎と「解らない」という答えの繰り返しである。それは、下のようにどうして(左)、解(右)の出現分布を見ればわかる。もちろん、「どうして」には「どうして...」も含まれれば、「どうしても」なども含まれる。また、「解」には「解らない、解る、誤解」などが含まれる。しかし、それらは大きく見れば実は同じようなものである、と思う。
 |  |
どうして(左)、解(右)の出現分布がよく似ているのがわかると思う。「どうして」と問いと「わからない」という答えはいつも対になるのである。
これらとちょうど反対の分布を示すのが「死、卒業」というキーワードだ。
 |  |
「どうして」(左)、「解」(右)という言葉が出現しない時には、「死」(左)、「卒業」(右)という言葉が現れるのである。また、この「死」(左)、「卒業」(右)という言葉が現れる時は、「先生」と「先生」である「私」があまり登場しない時でもある。学生である「私」から「先生」である「私」への過渡期であり、それは同時に「死」(左)、「卒業」(右)ということを浸透させる時期でもあるのだ。
結局、「どうして、解、死、卒業」は小説の最後において、同時に出現する。それらは最後に重なるのだ。それが答えなのか、あるいは答えがどこかに消えてしまったのか、どちらなのかはわからないままだ。
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
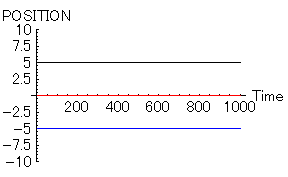 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
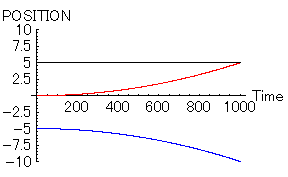 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
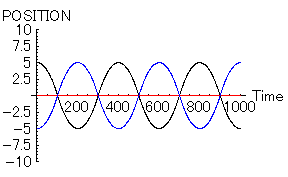 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
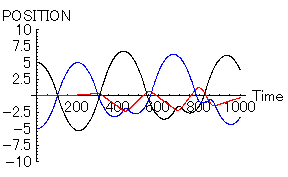 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)
2000-09-07[n年前へ]
■草枕で遊ぶ 
それが人間の科学なんだよ、と誰かが言った
どうしても割り切らないではいられない話だと知った時、それが人間の科学なんだよ、と...(半神)
私が大好きな演劇の一つに「半神」がある。レイ・ブラッドベリ・萩尾望都・野田秀樹の共作とも言うべきこの「半神」の中で1/2+ 1/2 = 2/4 という「螺旋方程式」の謎に対して
「その謎はひとごと(他人事)ではない。」というレトリックが使われていた。ここでは「ひとごと」という言葉の意味を巧みに切り替えて、「論理をすり替え」ている。こんなレトリックが私は気持ち良くて大好きだ。急斜面のコブを巧みにすり抜けていくスキーのモーグル選手みたいで、爽快な感じがするのである。
「ひとごと(人ごと)でないのだから、その謎は化け物に関わることだ。」
ところで野田秀樹ほど言葉遊びが巧みな人もそうそういないだろうが、この
「ひとごと(人ごと)でないのだから、その謎は化け物に関わることだ。」というもののオリジナルはもちろん夏目漱石の草枕の冒頭部だろう。その草枕の冒頭部分を部分的に抜粋するとこんな感じになる。
智に働けば角が立つ。情に棹させば流される。意地を通せば窮屈だ。とかくに人の世は住みにくい。人の世を作ったものは神でもなければ鬼でもない。やはり向う三軒両隣りにちらちらするただの人である。ただの人が作った人の世が住みにくいからとて、越す国はあるまい。あれば人でなしの国へ行くばかりだ。人でなしの国は人の世よりもなお住みにくかろう。
この
「人の世が住みにくい」という巧みな論理はどうだろうか?私には実に爽快な自然な飛躍に感じられる。目的とする場所へ、巧みに言葉を切り替えていくことで自然に辿り着くこんなやり方がとても気持ちが良い、と私は思う。
->「人が作った世が住みにくいならば、人でないものの世なら住みやすいだろうか」
-> 「人でなしの国へ行くばかり」
-> 「人でなしの国は人の世よりもなお住みにくい」
ところで、以前
でも挙げたとても面白いの中でもこの草枕冒頭部の論理のすり替えについて触れられていて、その中で漱石の「文学評論」中の「漱石とあたたかな科学」小山慶太著 講談社学術文庫
花は科学じゃない、しかし植物学は科学である。鳥は科学じゃない、しかし動物学は科学である。文学はもとより科学じゃない、しかし文学の批評または歴史は科学である。というレトリックに対しても
「文学のどこに観察、実験、数理解析が施せるのであろうか。」と書かれている。もちろん、「文学を味わうのは心であるべき」ということは言うまでもない。しかし、「文学のどこに観察、実験、数理解析が施せるのであろうか。」というところで思考を停止してしまうのは、実に残念であると私は思う。そこで、今回は「草枕」を題材に採って、いつものように単語解析をすることで、適当な考察をしてみることにした。「草枕」に対して数理解析をして遊んでみたい、と思うのである。
「草枕」は青年画家がブラブラしたり、ボうっと色々なことを考えたりする話だ。そして、いかに芸術が生まれるかということに考えてみたりするのである。例えば、冒頭では
住みにくさが高じると、安い所へ引き越したくなる。どこへ越しても住みにくいと悟った時、詩が生れて、画が出来る。という具合である。また、途中の部分では
して見ると四角な世界から常識と名のつく、一角を磨滅して、三角のうちに住むのを芸術家と呼んでもよかろう。というように書かれている。
一体、青年画家がどんな時に「画」を書くのかどうかを知るために、他の単語の出現分布と「画」の出現分布を調べてみることにした。今回、ノミネートしてみた単語は「角」・「男」・「女」である。
角が立つ四角い人の世の中で三角のうちに住むのが芸術家であるならば、その「角」と「画」の相関は調べてみたいと思うハズである。また、これまでに様々な「男」と「女」の関係を考えてきた「できるかな?」であるから、やはりここは「男」と「女」もノミネートしないわけにはいかないだろう。
そこで、「画」・「角」・「男」・「女」の各語の出現分布を調べてみたのが次の各図である。もちろん、今回も前回
と同じく、wordfreqを使って解析を行った。 |  |
 |  |
次に、「画」の出現分布に対するそれぞれの言葉の出現分布の相関値を計算してみよう(なお、計算の安定のために、適当な平滑化をここでは行っている。)主人公の青年画家がどんな時に「画」について考えたり、描こうとしたりするかを考えてみるわけである。その計算結果が次の表である。
角 | 男 | 女 | |
相関係数 | 0.08 | 0.09 | 0.21 |
そして、さらにこれをグラフにしてみたものが、下のグラフである。
 |
おやおや、困ったなぁ。ちょっと、この「画」と「女」の相関の高さはちょっと異常だなぁ。「角」や「男」の出現分布の「画」に対する相関は0.1以下であるが、何と「女」は0.2を越えている。最初は、「画」と「角」を強引に結びつけて話を終わらせるつもりでいたのになぁ。これじゃぁ、主人公はヒロインを前にするときだけ芸術家になるみたいじゃないの。おかしいなぁ、こんな狙いじゃなかったのになぁ...まるで、「草枕」は漱石の前田卓へのラブレターみたいに思えてきてしまうではありませんか...
う〜ん、これはどっか間違えたかなぁ。まぁ、いいや。今日はもう眠いし。
ところで、「草枕」ではどのようにして文学・音楽・絵画などのさまざまな芸術が生まれて来るかが書かれている。そして、冒頭の「半神」でも、シャム双生児の姉妹とともに「螺旋方程式」の謎を追いかけるうちに、人の心を動かす孤独と音が生まれてくるようすが語られていく。
 |
今回の相関解析では、「芸術は女を前にしたときに生まれる」というフザケタ結果に終わってしまったが、その真偽についてはまたいつか考えてみることにして、とりあえず今回は草枕の中の台詞で話を強引に終わらせたいと思う。
越す事のならぬ世が住みにくければ、住みにくい所をどれほどか、寛容て、束の間の命を、束の間でも住みよくせねばならぬ。ここに詩人という天職が出来て、ここに画家という使命が降る。あらゆる芸術の士は人の世を長閑にし、人の心を豊かにするが故に尊とい。
2001-12-24[n年前へ]
■즹닛 쫆쫦뾮 돑샮ꖹꗋꆼꖫꆼ쪸룋 
本屋で見てみることにしよう、というわけでメモ。狐罠 北森鴻 講談社文庫も探しているのだけれど、なかなか見つからない。 from 「今宵、Webの片隅で」