2004-07-03[n年前へ]
■青春18きっぷは定義式 
今年の春の青春18切符のコピー
√a = 18旅路(ルート)の中では、人はいつも18(age)である。に対してのツッコミ
ちなみにこの公式には”落とし穴”があり、普通に解くと「a=324」と答えが出てしまいます。誰がどのような旅をしても心の中ではいつも18歳、と伝えたいのでしょうか。を見る。
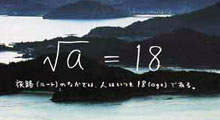 それは、"="の定義次第に違いない。このコピーの作者は実は数式処理系に堪能で、"="は、いわゆる等号"=="ではなく、代入の"="かもしれない。つまり、「√aというものは全て18が代入される」という手順を意味しているというのも自然かもしれない。
それは、"="の定義次第に違いない。このコピーの作者は実は数式処理系に堪能で、"="は、いわゆる等号"=="ではなく、代入の"="かもしれない。つまり、「√aというものは全て18が代入される」という手順を意味しているというのも自然かもしれない。そして、さらにこの式は"√"という演算子(もしくは関数)を定義する式であって、(例えばMathematicaなら)この式は
root(a_) := 18
なんていう内容を書いてある、とも自然に読むことができるだろう。すると、これは「ルートをとるとどんなaも全て18になる」という定義だ。もっと素直に言い換えれば、それはコピーそのままの「旅路(ルート)の中では、人は誰でも18(age)になる」である。そういう処理を行わせるものこそが「旅路(ルート)」というものなんだ、と高らかに定義・宣言する式である。
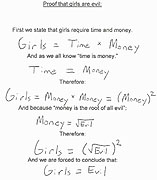 そして、(「女の子=悪」の証明風に言うのなら)「人のルート(root=根底にあるもの)はそんな18才の頃のようなものだ」とさらに想像してみるのはどうだろうか。青春18きっぷのポスターに書かれた小さな式は「旅は人を18歳の頃の気分にさせる。そして、それこそが人の根底にあるものなんだ」という言葉だと勝手に想像してみるのだって面白いはずだ。
そして、(「女の子=悪」の証明風に言うのなら)「人のルート(root=根底にあるもの)はそんな18才の頃のようなものだ」とさらに想像してみるのはどうだろうか。青春18きっぷのポスターに書かれた小さな式は「旅は人を18歳の頃の気分にさせる。そして、それこそが人の根底にあるものなんだ」という言葉だと勝手に想像してみるのだって面白いはずだ。青春18きっぷの公式から"a=324"なんてなんだか少しツマラナイ答えを導いてしまうのではなくて、もっと色んな想像をして色んな答えを導いてみるのも良いのじゃないかな、と思う。答えが(自分の知識の範疇で想像できる)一つだけなんていうのは「青春18きっぷ」には似合わない。もっと、色んな期待とともに線路の先を眺めた方が、きっと面白いことを見つけられるに違いない。
2008-06-09[n年前へ]
■Photoshopプラグイン開発環境(PDLS)再び 
 Photoshopプラグイン開発環境 Photoshop DLL Linking System (PDLS) のページを(旧Pukiwiki)のファイルを元に書き直しました。PDFの説明ファイルの2004/08/07版はこちらになります。また、サンプルソース・バイナリファイルはこちらです。
Photoshopプラグイン開発環境 Photoshop DLL Linking System (PDLS) のページを(旧Pukiwiki)のファイルを元に書き直しました。PDFの説明ファイルの2004/08/07版はこちらになります。また、サンプルソース・バイナリファイルはこちらです。
 AmetMultiのモットーは「ATOKから何でもできる」でしたが、PDLSのモットーは「Photoshopから(その人のレベルに応じて)何でもできる」でした。(Photoshopの規約は気にせず)Cを使ってネイティブ・プラグインを気軽に書くこともできれば、GUIを使った連続作業などで自動的にマクロ関数(プラグイン)をお手軽に作ることもできる。その人のレベルに応じて、ステップアップすることができるPhotoshopのプラグイン開発環境というわけです。
AmetMultiのモットーは「ATOKから何でもできる」でしたが、PDLSのモットーは「Photoshopから(その人のレベルに応じて)何でもできる」でした。(Photoshopの規約は気にせず)Cを使ってネイティブ・プラグインを気軽に書くこともできれば、GUIを使った連続作業などで自動的にマクロ関数(プラグイン)をお手軽に作ることもできる。その人のレベルに応じて、ステップアップすることができるPhotoshopのプラグイン開発環境というわけです。
 マクロ関数やネイティブ・プラグインを組み合わせれば、さらにカスタムプラグインを作ることもできます。また変数を使ったり演算や数式処理も使えて、NEWやDELETEといったマクロを使い、局所領域に対してだけ演算を行うこともできます。そして、マクロプラグインには自動的にGUIをかぶせることもできるのです(GUIコードを書かなくても、ダイアログで変数設定などを実行時にすることができる)。
マクロ関数やネイティブ・プラグインを組み合わせれば、さらにカスタムプラグインを作ることもできます。また変数を使ったり演算や数式処理も使えて、NEWやDELETEといったマクロを使い、局所領域に対してだけ演算を行うこともできます。そして、マクロプラグインには自動的にGUIをかぶせることもできるのです(GUIコードを書かなくても、ダイアログで変数設定などを実行時にすることができる)。
 また、表計算アプリとの連携や鳥瞰図表示のプラグインもついている……というテキトーな機能てんこ盛り、の環境です。Photoshop Elementなんかで使うこともできますので、画像処理で遊んでみたい人は一度使ってみても良いかもしれません。いつものように、SYSTEMコールもできるプラグインなので、つまりは何でもし放題のプラグイン環境です。使ったことのないPhotoshopユーザ(ないしはPhotoshopプラグイン互換の画像処理ソフトユーザ)は一度遊んでみると良いかもしれません。
また、表計算アプリとの連携や鳥瞰図表示のプラグインもついている……というテキトーな機能てんこ盛り、の環境です。Photoshop Elementなんかで使うこともできますので、画像処理で遊んでみたい人は一度使ってみても良いかもしれません。いつものように、SYSTEMコールもできるプラグインなので、つまりは何でもし放題のプラグイン環境です。使ったことのないPhotoshopユーザ(ないしはPhotoshopプラグイン互換の画像処理ソフトユーザ)は一度遊んでみると良いかもしれません。
2008-06-28[n年前へ]
■「Mathematica開発者のウルフラム」と「ファインマン」 
 今週頭に「数式処理アプリケーションのMathematicaが最初にリリースされてから、今日で20年たちました」と、開発者Stephen WolframからMathematicaユーザにメールが送られてきた。スティーブン・ウルフラムが28才の時の1988年の6月23日にMathematica 1.0 が出荷されたのである。
今週頭に「数式処理アプリケーションのMathematicaが最初にリリースされてから、今日で20年たちました」と、開発者Stephen WolframからMathematicaユーザにメールが送られてきた。スティーブン・ウルフラムが28才の時の1988年の6月23日にMathematica 1.0 が出荷されたのである。
For twenty years we've pursued our long-term vision for Mathematica.
Mathematicaは結局のところ、パターンマッチングを延々と行うプログラムである。データベースに登録されているパターン・規則にもどづいて、与えられた数式を置換していくことにより、Mathematicaは解(や所望の結果)を得る。
 ところで、「ファインマン物理学」で有名なR.P.ファインマンはカリフォルニア工科大学で1983年から1985年までの間、計算機科学の講義(ファインマン計算機科学)をしている。その頃の学生がスティーブン・ウルフラムである。
ところで、「ファインマン物理学」で有名なR.P.ファインマンはカリフォルニア工科大学で1983年から1985年までの間、計算機科学の講義(ファインマン計算機科学)をしている。その頃の学生がスティーブン・ウルフラムである。
ファインマンは「科学とは何か」の中で、「数学とはパターンにすぎない」「数学とはパターンを探すことだ」と端的に短く書き表している。この言葉を思い起こしながら、(おそらくそんな言葉を聞いていただろう)彼の学生でもあったウルフラムが「パターンマッチングによる数式処理アプリケーション」を商品化し市場に広まらせたのだ、と考えてみると何だか「面白い繋がり」を感じる。そんな繋がりを思い浮かべながら、Mathematicaの20年を集めたスクラップブック を眺めてみると、きっと楽しいと思う。
I'm looking forward to the next 20 years and hope that you'll continue to follow Mathematica on this exciting journey.
-- Stephen Wolfram
2008-11-14[n年前へ]
■「色を変える"宝石"ガーネット」と「"変化"するMathematica」 
 「色を変える"宝石"ガーネット」の光吸収スペクトルを探すうちに、こんなページやこういったページに出会いました。こういうページを眺めていると、単純な色名では表現できない宝石の光吸収スペクトルを(数式処理プログラムの)Mathematicaで関数にして、さまざまな照明の中で、宝石が外に見せる色を計算するライブラリを作りたい、と思ったりします。
「色を変える"宝石"ガーネット」の光吸収スペクトルを探すうちに、こんなページやこういったページに出会いました。こういうページを眺めていると、単純な色名では表現できない宝石の光吸収スペクトルを(数式処理プログラムの)Mathematicaで関数にして、さまざまな照明の中で、宝石が外に見せる色を計算するライブラリを作りたい、と思ったりします。
光吸収スペクトルは変わらなくても、照明光スペクトルや視覚スペクトルに依存して「見た感じ」が変わるようすをMathematicaで描いてみたいと思ったわけです。
 そんなことを思いながら、もうすぐ公開される Mathematica の新バージョン、バージョン7を見ました。そのMathematicaが"変化"し続けるさまは、なぜか「色を変える"宝石"ガーネット」を連想させました。さまざまな機能が追加され、姿・見た目が大きく変わっているように見えても、少しその新たな装いを脱がしてみると、その下にはこれまで同じ「HEADで表現される構造が組み合わさったオブジェクト」が見えてきて、そこに色を変える宝石と同じさまを感じたのです。
そんなことを思いながら、もうすぐ公開される Mathematica の新バージョン、バージョン7を見ました。そのMathematicaが"変化"し続けるさまは、なぜか「色を変える"宝石"ガーネット」を連想させました。さまざまな機能が追加され、姿・見た目が大きく変わっているように見えても、少しその新たな装いを脱がしてみると、その下にはこれまで同じ「HEADで表現される構造が組み合わさったオブジェクト」が見えてきて、そこに色を変える宝石と同じさまを感じたのです。
色鮮やかに映える機能をとても魅力的に感じる人は、多いことでしょう。その一方で、特に変化するわけでもない内部の光吸収スペクトルや基本オブジェクト構造に不思議に心惹かれる人もいるように思います。「さまざまな機能を使って何かをしたい」と思う人もいれば、「基本構造を組み合わせて何かを作ってみたい」と思う人もいそうな気がします。
もちろん、その時の気分で「どっちが好き」かは変わることも多いかもしれません。このページを読む人は技術系の人が多いと思いますが、(この瞬間の)あなたなら「どちら」を好むのでしょう。どちらを選ぶのでしょうか?
2009-04-09[n年前へ]
■Mathematica Player と Player Pro の互換性に関する開発者用ガイドライン(と比較表) 
Mathematica Player と Player Pro の互換性に関する開発者用ガイドライン、Player,Player Pro,Mathematica の違いの比較表、FAQ