1999-01-10[n年前へ]
■宇宙人はどこにいる? 
画像復元を勉強してみたい その1
知人から「自称UFO写真」というのものが冗談半分(いや100%位か)で送られてきた。その写真はボケボケの画像なので何がなんだかなんだかわからない。そこで、ぼけぼけ画像を復元する方法を勉強してみたい。UFOは冗談として、画像復元において進んでいるのは天文分野である。そこで、このようなタイトルなのである。もちろん、画像復元の問題は奥が深すぎるので、じっくりと時間をかけてみる。今回はMathematicaを使って試行錯誤を行った。
ボケ画像を復元するには、ボケ画像がどのように出来ているかを考えなければならない。そこで、ごく単純なぼけ画像を考えてみる。まずは以下の画像のような場合である。
 |  |
 |  |
画像:1のような点画像が、画像:2のような分布のボケ画像になるとすると、次のような関係が成り立つ。
(式:1) 画像:4 = 画像:3 * 画像:2
画像:1のような点画像が画像:2になるなら、それを参照すれば、画像:3のような点画像の集合がどう
ボケるかは計算できる。つまり、それが画像:4になる。ここで、*はコンボリューションを表している。
よくある信号処理の話で言えば、画像:2はインパルス応答である。といっても、これはごくごく単純な場合(線形シフトインバリアントとかいろいろ条件がある)の話である。まずはそういう簡単な場合から始めてみる。
このようなごく単純な場合には
(式:2) 画像:3 = 画像:4 * (1/画像:2)
とすれば、画像:3を復元できることになる。
そこで、まずは単純な1次元データで考える。下の画像:5のようにボケる場合を考える。ここでは、ガウス分布にボケるようにしてある。
 |
であったが、* すなわち、コンボリューションは
逆フーリエ変換(フーリエ変換(オリジナル画像) x フーリエ変換(ボケ具合))
と表すことができる。つまり、周波数領域で掛け算をすれば良いわけである。
 |  |
それでは、試しに適当な1次元データをつくって、画像:6とコンボリューションをとってやり、ボケさせてみる。
 |  |
逆フーリエ変換(フーリエ変換(画像:9) / フーリエ変換(画像:7))
= InverseFourier[Fourier[Image8] / Fourier[Image6]]; (*Mathematica*)
とやると、次のデータが得られる。
 |
(式:2) 画像:3 = 画像:4 * (1/画像:2)
を見るとわかるが、画像:2が周波数領域で0になる点があったりすると、計算することができない。また、0に近いとむやみな高周波数の増幅が行われて使えない。
そこで、この方法の修正として、ウィーナフィルターなどの最小平均自乗誤差フィルターがある。これにも多くの不自然な条件のもとに計算される(らしい)。しかし、infoseek辺りで探した限りでは、ウィーナフィルターを用いた画像復元の標準であるらしい。
この方法は先の逆変換に対して、次のように変形されたものである。Mathematicaの表記をそのまま貼り付けたのでわかりにくいかもしれない。
Noise ノイズのパワースペクトル
Signal 信号のパワースペクトル
Boke ボケる様子のインパルス応答
Conjugate 複素共役
BokeData ボケ画像
ResData1 計算した復元画像
Boke1 = (Boke^2 + Noise/Signal)/Conjugate[Boke]; (*Mathematica*)
ResData1 = InverseFourier[Fourier[BokeData] / Fourier[Boke1]]; (*Mathematica*)
である。Noise/SignalはS/N比の逆数であるから、SN比の大きいところではインバースフィルターに近づく。また、インバースフィルターの計算不能な点が消えている。
これを使って復元してみたのが、次のデータである。
 |
まずは、ボケのフィルター(PSF=PointSpreadFunction(どのようにボケるかを示すもの)、2次元のインパルス応答)である。
 |
 |  |
 |
その他線形の画像復元法をいくつか調べたが、ウィーナフィルターやインバースフィルターとほとんど同じような物が(素人目には)多かった。そこで、ウィーナフィルタなどとはやり方がかなり異なるものについて、いずれ挑戦してみたい。
関係はないが、ウィナーと言えばサイバネティクスが思い浮かんでしまう。当然、ロゲルギストが連想されるわけだが、文庫本か何かで岩波版と中公版の「物理の散歩道」が安く売り出されないのだろうか?売れると思うんだけど。新書版は高すぎる。
宇宙人はどこにいるか? そういった話は専門家に聞いて欲しい。わからないとは思うが。
さて、ここからは、1999.01.24に書いている。シンクロニシティとでも言うのか、今回の一週間後の1999.01.17に
日本テレビ系『特命リサーチ200X』で
地球外生命体は存在するのか?( http://www.ntv.co.jp/FERC/research/19990117/f0220.html )
という回があった。何とこの回のコメンテーターは先の専門家と同じなのだ。偶然とは面白いものだ。
1999-07-24[n年前へ]
■視点 
ここにいるよ

長野県の須玉にある病院で撮影した写真である。古い顕微鏡を光が照らそうとしている。顕微鏡を覗いてみたが、レンズが汚れているせいかうまく焦点を合わせることができなかった。光学系にとって焦点をいかに先鋭にするかは一番苦労するところである。
景色に焦点を合わせて、フィルムに結像させるのがカメラだ。しかし、フィルムに写っているのは単なる景色ではない。カメラの光が集まる焦点にフィルムが位置していると思い込むとわからなくなる。逆から考えてみれば簡単に判るはずだ。カメラの視点にフィルムが位置しているのだ。フィルムに景色が写っているのではなく、フィルムが景色を選び、景色を切り取っているのである。
写真に写っているのは、撮影者の視点なのである。写真を見れば、撮影者が、どこに立ち、何を見てるかが浮かび上がってくるはずである。フィルムに写っているのは撮影者自身なのだ。
1999-08-08[n年前へ]
■瞳の中の真実 
目の屈折率を調べよう
先日、近所の海へ行ってきた。水中メガネで覗いているとまるで熱帯魚みたいな魚が泳いでいて素敵なのだ。水中メガネを使うか使わないかで、海の楽しさは雲泥の差である。水中メガネで覗いてみると、裸眼の時とは別世界のようにくっきり見えるのである。
 |
さて、「水中視の光学」と言えば、物理の散歩道の「アユと泳ぐ」(新物理の散歩道-第2集- 中央公論社)に詳しく面白い考察がされている。本WEBでもScrapsにて「焦点」ということを考えたばかりなので、「アユと泳ぐ」と同様の解析を「できるかな?」風に行ってみたい。光学シミュレーターを作ってみたいのである。そのために、まずは人間の目の中の屈折率を調べなければならないだろう。というわけで、今回は下調べ編である。
それでは、人間の左目の水平方向の断面図を調べてみる。
 |
この中で普通のカメラでいうレンズの役割を果たしているのはどこだろうか。レンズの部分を赤く塗るとどのようになるだろうか?下に並べた3つのうちどれだと思われるだろうか。
A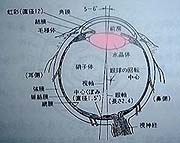 | B | C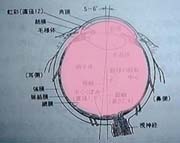 |
まずは、目の中の物質の屈折率を調べてみると、以下のようになる。
| 場所 | 屈折率 |
| 角膜 | 1.376 |
| 眼房 | 1.336 |
| 水晶体 | 1.386 |
| 硝子体 | 1.336 |
空気(15℃の乾燥空気)の屈折率はほぼ1.0であるから、空気と比較するならば、目の中の物質はほぼ同じ屈折率を持つといっても良い。角膜も眼房も水晶体も硝子体も同じ屈折率を持つとして良いだろう。すなわち、大雑把な近似においては図.2のCに示したようなピンク色のレンズがあるとして良い。つまり、目全体がレンズであり、レンズ面に焦点を結ぶようになっているのである。水晶体は若干の補正を行うに過ぎない。レンズの焦点はレンズから離れた場所にあるはずと思っている人もいるかもしれないが、レンズの表面に焦点があるものも実はよく使われている。
さて、人間が水の中に入るとどうなるだろうか?水は1.333(589.3nmの波長の光に対して)の屈折率を持つ。これは人間の目の中の物質の屈折率とほぼ同じである。水を主体として出来ている人間なのだからこれは当然だろう。しかしこれでは、目は光を屈折させることはほとんどできなくなる。そのため、水の中に入るときには水中メガネなどで目の回りを空気で満たしてやることが必要なのである。
本題からははずれるが、資料を眺めていると、面白いグラフが目に入ってきた。人間の目の断面方向の視細胞個数の分布を示したものであり、錐体と桿体を個別に示してある。「盲点」なんかも図中にある。
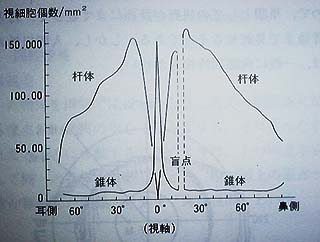 |
目に映る明るさって何ですか? - 君は天然色 - (1999.07.05)
の回に錐体と桿体については触れたが、桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上で働く。従って暗いものを見るには桿体の働きが重要になるわけだが、上のグラフは桿体が視点の中心にはほとんど存在していないことを示している。
従って、暗い所でものを見る際には、視点の中心では感度が足りなくなりやすいことがわかる。これまで、暗い星を眺めるときに視界の中心で見ようとすると見えないのだが、少し視点をずらしてやると見えるような気がしていたのだが、それは気のせいでは無かったようである。
さてさて、資料集めも終わったので「瞳シミュレーションソフトウェア」の開発に着手したいと思う。もちろん、時間がかかるのはいつものことだ。すぐにはできないけどね。
1999-08-20[n年前へ]
■色空間の世界へ (色弱と色空間 その3) 
Someday
今回は、
色を伝える時に、考え忘れていたこと(色弱と色空間 その1) - We can work it out! - (1999.08.09)
で行った計算を少し改良し、なおかつ色空間の世界を自由自在に動かしてみたいと思う。今回のメインは「立体グリグリ」のテストである。
まずは、前回と今回の計算の違いは、
- 前回はL,M,Sの各錐体の波長感度特性はRed,Green,Blueの単波長であるという仮定の元の計算
- 今回はL,M,Sの各錐体の波長感度特性はRed,Green,Blueの単波長とは異なるという条件での計算
- X= 0.412391R + 0.357584G + 0.180481B
- Y= 0.212639R + 0.715169G + 0.072192B
- Z= 0.019331R + 0.119195G + 0.950532B
- l = 0.16*X + 0.54*Y - 0.033*Z
- m = -0.16*X + 0.46*Y+0.033*Z
- s = Z
それでは、通常のRGB色空間と第1色盲(赤色盲)のRGB色空間を以下に示してみる。今回はMathematicaの出力をJavaAppletで動かすことができるLiveGraphics3Dを使用している。そのため、RGB色空間をグリグリ動かすことができる。それどころか、ステレオ画像にしてグリグリ動かすこともできる。ステレオ画像の見方は交差法である。ぜひ、試してもらいたい。
下のグラフの操作方法は
- 操作 = 作用
- マウス左ボタンドラッグ = 回転
- シフトキー + 垂直ドラッグ = ズームイン・アウト
- シフトキー + 水平ドラッグ = 垂直軸についての回転
- コントロールキー + 垂直ドラッグ = 焦点距離の変更
- マウス右ボタン垂直ドラッグ = 部品除去
- "s"キー = ステレオ画像作成
PageLiveGraphics3D
( http://www.nikonet.or.jp/spring/sanae/LiveGraphic3D/LiveGraphic3D.htm)
を参考にして欲しい。それでは、RGB色空間(ハリボテバージョン)を自由自在に動かしてみよう。
|
|
どうだろうか? RGB色空間を自由自在に動かせただろうか? 立体グリグリはできただろうか? 「ハリボテでつまらない」なんていう文句がある人もいるかもしれないが、気が向けば立方体の全面について描画を行うよう変更するつもりである。
こういった、Javaなどを使用した立体表現は表現力が非常に高い。しかし、読み手によっては必ず見れるとは限らないところが難しいところである。読み手を限定してしまう可能性が有る。それは、まさに色覚異常に関する問題と同じである。
TVが白黒放送からカラー放送に移行する当時は、カラー放送においても白黒TVでもきちんと識別できる色を考慮しながら放送しようとしていた、と聞く。白黒TVで観ている人が困らないようにである。しかし、現在はどうだろうか? 白黒TVで観ている人のことを考慮したTVなどほとんど無いのではないのではないか?
TV放送に限らずWEB、プレゼンテーションなどにおいて、最新の可能性と広い互換性を両立させていくためには、他の人を配慮する力が必要だと思う。そういう点においても非常に優れ、私がとても好きなWEBサイトが今日から一時停止してしまった。非常にさみしい。
それでは、今回の色空間自由自在はこんな所で終わりにしたい。
2000-01-13[n年前へ]
■WEBサイトの絆 
WEBの世界を可視化しよう
目に見えないものを実感できるものにしようと思うことは多い。「直接感じることが出来ないものを感じられる形にする」という作業とその結果には非常にわくわくさせられる。それは、きっと私だけではないと思う。
目に見えないものは色々ある。可視化して見てみたいものは多々あるのだが、以前、
の時に扱った、WEBのトポロジーなどもその最たるものである。WEBページはもちろん目に見えるわけではあるが、それらがどう繋がっているか、すなわち、WEB[= クモの巣(状の物);織物 ]そのものは目には見えない。ネットワークという目に見えない世界でWEBサイト同士がどう繋がっているか、それは企業のWEBサイト同士であれば企業間の繋がりを示すかもしれないし、公的機関のWEBであれば公的機関内部の繋がりが見えてくるかもしれない。そして、個人WEBであれば、個人どうしの繋がりが見えてくるだろう。そして、さらに考えを進めるならば、それが「WEBの繋がりだ」と端的に言い切ってしまっても良いと思う。
そういう色々なWEBサイト同士が互いに結びつき合う、つまりWEBそのものを今回は可視化してみたい。その結果はきっと「WEBサイトの絆」を私に見せてくれるはずだ。
例えば、ファイルシステムを可視化するものであれば、
- xcruise( http://tanaka-www.cs.titech.ac.jp/~euske/index-j.html )
そして、今回の本題のWEBサイトのHyperlink構造を可視化するソフトウェアも、少し探しただけでも結構ある。例えば、
- Site Manager
- ( http://www.sgi.com/software/sitemgr.html )
- HyperLINKWWW Visualization/Navigation
- ( http://www.acl.lanl.gov/%7Ekeahey/c3/navigate/navigate.html )
しかし、よく調べていないので間違っているかもしれないが、この辺りのソフト(appleを除く)はWEBサイト内のリンクのみに限られるようである。それでは、今回の目的とは違う。何しろ、今回知りたいのはWEBサイト同士のリンクの度合いである。WEBのトポロジーなのである。
そこで、もう少し探してみる。すると、今回の目的にかなり近い情報が
- Web構造の把握 宮久地博臣 都立科学技術大学大学院 平成9年度修士論文
- ( http://home2.highway.ne.jp/miyakuji/shuron.html )
やり方はどうしたら良いだろうか?宮久地氏と同じようにWeb Robotを作成して、データを集めるのが理想的だろう。しかし、「perl入門」を昨日やっと買ったばかりの私にはとても難しそうである。いや、もしそんなことをしたらとんでもないことになるに違いない。
そこで、perlのlwp-rgetを用いて各WEBの内容をローカルのPC内にダウンロードした上で、勉強がてらperlで解析を行うことにした。と、思ったのだが、lwp-rgetが上手く動いてくれない。まだドキュメントをちゃんと読んでいないせいだろうか?何故か、ダウンロードの途中で終了してしまう。仕方がないので、急遽作戦を変更し、ダウンロード作業はlwp-rgetではなくてwgetを用いることにした。
行った手順は以下のようになる。
- 5つのWEBサイトを広いWEB内から適当に選択する
- 選んだ各WEBサイト内のファイルについて、相互のハイパーリンクを抽出し、その数を解析する
- その結果を可視化する
以下に、解析を行った結果、すなわちサイトA,B,C,D,Eの相互に対するリンク数を示す。
| ↓から→へのリンク数 | |||||
0 | 2 | 0 | 27 | ||
1 | 0 | 13 | 273 | ||
20 | 2 | 0 | 43 | ||
0 | 11 | 0 | 285 | ||
1 | 1 | 1 | 1 | ||
合計 | 22 | 14 | 3 | 14 | / |
サイトE「日記猿人」へのリンクがムチャクチャ多いのは投票ボタンという形で、他のサイトからリンクがなされているからである。
さて、上の表からではWEBの絆を実感できないので、「WEBの絆」を3次元空間に可視化するJavaアプレットを以下に張り付けておく。WEBサイトが5つあるので、それぞれのサイトをピラミッド構造(四角柱状)に配置した。
各WEBサイトの表示色は、
- A = 赤
- B = 緑
- C = 青
- D = 黄
- E = 灰
それぞれのサイトから伸びる直線の長さは、そのサイトから他のサイトへ向かうリンク数に比例したものにしている。また、直線の太さもリンク数に比例させている。また、それぞれのWEBサイトを示す立方体の大きさは自分へ向かうリンク数に比例させている。ただし、サイトEの大きさはあまりにも巨大なため、リンク数に比例したものにはなっていない。また、サイトE、すなわち「日記猿人」、へのリンクは省略し、全てサイトEからの直線リンクを表示するだけにした。
さぁ、WEBサイトの構造を自分の目でみて、そしてグリグリ動かして見てもらいたい。このグラフの操作方法は
- 操作 = 作用
- マウス左ボタンドラッグ = 回転
- シフトキー + 垂直ドラッグ = ズームイン・アウト
- シフトキー + 水平ドラッグ = 垂直軸についての回転
- コントロールキー + 垂直ドラッグ = 焦点距離の変更
- マウス右ボタン垂直ドラッグ = 部品除去
- "s"キー = ステレオ画像作成
Java表示が上手く動かない人のために、静止画も一応張り込んでおく。
 |
どうだろう?この5つのWEB間のWEB構造から何が見えるだろうか?こういう解析を数多くのサイトに行うと非常に面白い結果が得られそうである。特に「日記猿人」のようなコミュニティーに対して行うと興味深い結果が得られるはずだ。
私のような「日記猿人」の日記はほとんど読まない(サイトAに関しては大ファンであるが)人間にとっても興味深いのであるから、関係者にとってはきっと...の筈だ。
さて、今回はテストのためにごく少数(5つ)のWEBの解析を行ってみた。いつか、こういった解析を広い範囲で行い、そして、時系列的な変化をも調べようと思う。銀河のvoid構造が観測され、可視化されたものを見たときもとてもわくわくしたものだが、WEBの構造・変化ならばどうだろうか?
不思議なことに、そういうことを考えていると、「新宿都庁」と「思い出横町」が頭の中に浮かんできてしまうのは何故だろうか?押井守の影響だろうか。謎である。
そして、こうも思う。WEBネットワークの中でWEBサイトは何を感じているのだろうか?これらのWEBサイトはもしかしたら孤独を感じているのだろうか、それとも繋がりを感じているのだろうか?あの時のページの中の一フレーズがその答えの一つなのかもしれない。