hirax.net::Keywords::「色覚」のブログ

■目に映る明るさって何ですか?　

君は天然色

　前回、
デジカメ画像をスクリーンセーバーにしたい-記念写真を飾ろう - (1999.06.30)
を作るために、いくつか調べ事をした(ホントはずっと昔に)。それについてまとめておきたい。
調べたことは、

• カラーから白黒への変換はどうする?
• セピアカラーって一体何だ。
• セピアカラーへの変換はどうやろう?

こんな感じだ。今回はその第1回目の「カラーから白黒への変換はどうする?」である。

　カラーから白黒への変換はどうする? どうしよう?　これは結構難しい問題(結果的にやったことは簡単でも、プロセスとしてはすごく難しい)だ。そうそう白黒の世界を見たことのある人はいないだろう。特殊な状況下(たとえば、すごく暗い所とか)では色を感じないこともあるだろうが、普通の世界は天然色である。フルカラーの世界だ。そもそも明るさって一体何だ?(明快に答えられる方教えてください。)　例えば、下の図で明るい順番はどうなっているだろうか?自信を持って答えられるだろうか。

明るい順番は?

　とグチを言っていてもしょうがないから、決めてしまおう。うす暗い(1lx程度)部屋で景色を眺めてみよう。その時見える世界が、明るさの世界だ。そこには色など存在しない。確かめて欲しい。今回は、とにかくそれを「明るさ」の尺度としてしまおう。
(興味ある方は明るさを測ろう- 新技術の女神 -(1998.11.13)もご覧下さい)
　次に明るい部屋へ移動する。そこでは、新たなものが加わる。それが「色」である。ということで、「明るさ」+「色」で世界を表現することにしよう。

　いきなりではあるが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。

霊長類網膜内の錐体と桿体

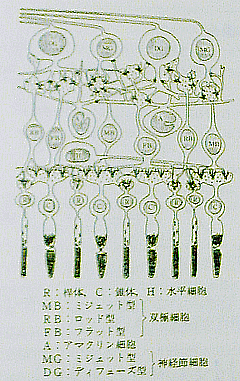「視覚と画像」　大頭・行田　著　森北出版より

桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上の所で働き色に対して反応する。従って、暗い部屋では桿体のみが働くため、明るさはわかるが色を認識することができない。というわけで、先ほどの「暗い部屋では...」の例え話に繋がるわけである。

　それでは、明るい部屋で感じる色はどうなっているだろうか。色を感じる錐体の中には波長感度の異なる3種類の視物質がある。それぞれの波長感度を以下に示す。

3種類の視物質の波長感度

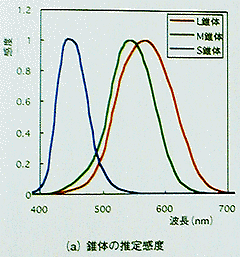CQ出版 洪　博哲著　「お話・カラー画像処理」より

　次に、それらの3種類の視物質による錐体が組み合わさった時の波長比視感度を以下に示す。点線で示してあるほうは比較的暗い場所での波長比視感度なので、今回は無視して欲しい。

標準比視感度

「視覚と画像」　大頭・行田　著　森北出版より

　後は、このグラフを元に赤、緑、青の3点で重み付けしてやれば良いだろう。

というわけで、グレー化のために使っているのはこの式だ。

• Red: ptr[2]
• Green: ptr[1]
• Blue: ptr[0]、として

ptr[1] = ptr[0] = ptr[2] = 0.3*ptr[2]+0.59*ptr[1]+0.11*ptr[0];
　やっと、ここまで辿りついた。結局使うのはこんな簡単な式なんだ、っていうツッコミは無しにして欲しい。同じ式を使うのでも、私はそこまでのプロセスも重視したいのだ。

　さて、こういった色を扱う話題であれば、脇色彩研究所のWEB(http://www.mmjp.or.jp/rwicp/ )中から

• 色に対する感じ方（眼とフィルム）( http://www.mmjp.or.jp/rwicp/data106.html )
• カラーフィルムの特性と色再現( http://www.mmjp.or.jp/rwicp/filmirosai.html )
• 明るさの見え方（明暗対比）( http://www.mmjp.or.jp/rwicp/data506.html )
• 色覚、眼の色に対する感じ方( http://www.mmjp.or.jp/rwicp/data509.html )

といった項目が参考になるだろう。これまで、とある事情によりこのWEBを紹介できなかったが、これからは紹介し放題だ。
　また、文中でも書いたが、「明るさとは***ということだ」と明快に答えられる方は私に是非教えて頂きたい。もし、素晴らしい答えが頂けたら、粗品(言葉通りの)を進呈しても良いと思っているくらいだ。

　なお、以下のような答え方は遠慮致したい。

例1:
私 「液体と固体はどう区別するの」
A 「融点を境にして上と下」
私 「....」

例2:
私 「クジラは哺乳類、魚類どっち?」
A 「卵生まないから哺乳類」
私 「...」

■色を伝える時に、考え忘れていたこと(色弱と色空間 その1)　

We can work it out!

　オプトニューズ (1999) No.4の光の話題に三楽病院の岡島修氏が「レーザポインタと色覚異常」という小文を書いている。色弱の人の感じ方とプレゼンテーション(特にレーザポインタの色)に関する提言である。それを読んであることを思い出した。何年か前、Labofinder(Macintoshを科学分野で使うユーザーグループ)でプレゼンテーションについて特集していた発表会だったと思う。どなたかが発表を行った後に、次のような質問があった。

　「私は色弱なのですが、プレゼンテーションを行う際に使う色などについて、そのような人を意識して作成されているでしょうか?」

　恥ずかしいことに、私はあまり考えたことがなかった。そして、本WEBを作るに際してもそういった点はおろそかになっていると思う。そういう自分自身への反省を込めて、色弱と色空間について考えてみたいと思う。

　まずは、色弱に関する情報を調べよう。

• COLOR HANDICAP( http://www.sakuranet.or.jp/~tks/color/text/ )
• からーふぃくしょん( http://sun.endless.ne.jp/users/tanafic/ )
• Dr.MeMeの おめめ講座　　(http://www.so-net.ne.jp/vivre/eye/ )

といった辺りから簡単な知識を得る。

　それでは、私なりの理解と考察を始めてみたい。
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
の回で触れたが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。この内、色(すなわち光の波長方向に関する感じ方)を感じるのは、錐体の働きによるものである。錐体には3種類有り、

• L錐体 -> 赤
• M錐 -> 緑
• S錐体 -> 青

という波長感度を持っている(それぞれの波長感度については
目に映る明るさって何ですか? - 君は天然色- (1999.07.05)
を参照のこと)。それらの錐体に異常がある時に、色弱もしくは色盲が発生する。

色覚異常の種類

L錐体 (赤)	M錐体	S錐体	先天性色覚異常の分類
O	O	O	正常
X	X	X	桿体1色覚 (全色盲)
O	X	X	錐体1色覚 (赤)
X	O	X	錐体1色覚 (緑)
X	X	O	錐体1色覚 (青)
X	O	O	第1色盲 (赤色盲)
O	X	O	第2色盲 (緑色盲)
O	O	X	第3色盲 (青色盲)
OX	O	O	第1色弱 (赤色弱)
O	OX	O	第2色弱 (緑色弱)
O	O	OX	第3色弱 (青色弱)

　この図中でOは正常、Xは欠損、OXは機能低下である。

　M,L錐体に関する異常はX染色体劣勢遺伝をする。また、錐体1色覚、および、S錐体に異常がある第3色盲・第3色弱は比較的少ないという。

　それでは、これらの錐体に異常があるとどのような色を識別できなくなるのだろうか?　私は先に挙げたようなWEBを読んだくらいの知識がないので、数学的な考察をおこなってみる。現実をよく知らないため、実際の症例とはかなりの違いがあるかもしれない、ということは先に断っておく。

　現実の症例の参考としては、岡島修氏の「レーザポインタと色覚異常」中に挙げられているCIEXYZ表色系における強度色覚異常者(第1異常、および、第2異常)の混同色を用いる。その図を加工し、XY色度図を重ねたものを以下に示す。それぞれの図において、白い直線上の色を混同してしまうのである。

CIE XYZ表色系における強度色覚異常者(第1異常、および、第2異常)の混同色

第1異常

第2異常

　今回は、通常の(Red,Green,Blue)データを基本として考える。PCなどで表示を行う際に一番よく使うからである。任意のRGBデータをCIEXYZ表色系に直すためには、
WEBページは会社の顔色 -WEBページの色空間を考える2- (1999.04.26)
で用いたハイビジョンTVの色空間を例に用いて、

• Ｘ＝ 0.412391R + 0.357584G + 0.180481B
• Ｙ＝ 0.212639R + 0.715169G + 0.072192B
• Ｚ＝ 0.019331R + 0.119195G + 0.950532B

というRGBから3刺激値への変形を行い、その後に

• x=X/(X+Y+Z)
• y=Y/(X+Y+Z)

という式を用いて、xy色度座標への変換を行う。なお、x,y色度座標では座標が一つ減っていることでわかるかと思うが、xy色度座標だけでは明るさが違う色が同じ点に存在することになる。そこで、今回は一番明るい条件の色を用いている。

　それでは、通常、第1色盲(赤色盲)、第2色盲(緑色盲)の3種類についてxy色度図の計算例を示してみる。ある錐体に異常が存在する場合に、どのような色空間が再現されるかの計算を行ってみる。通常のxy色度の位置において、ある錐体の刺激を無くした場合に色がどう変化するかを示したものである。であるから、第1色盲(赤色盲)、第2色盲(緑色盲)においては通常使われるxy色度図とは異なるものになる。また、ここで示した色が色弱の人が見ている色という意味でもない。

　単純に、ある錐体が得るであろう情報を無くしたときに、情報の識別がどのように困難になるかを確認した、と言った方がいいかもしれない。

　また、本来3錐体の波長感度特性はRed,Green,Blueの単波長というわけでもない。しかし、今回は簡単のために、3錐体の波長感度特性はRed,Green,Blueの単波長であるという仮定の元に計算を行っている。そのため、かなり現実とは違う結果になっている。近々、きちんとした計算をするつもりである。

xy色度図の計算例

通常

第1色盲(赤色盲)

第2色盲(緑色盲)

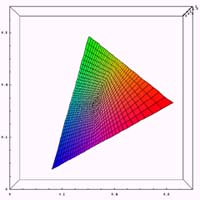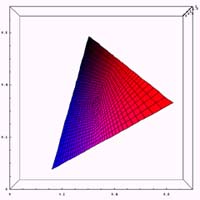　ここでは、Z方向(明るさ方向)に対して無視を行っているので、かなりの誤差が存在すると思う。また、計算の中で一つの錐体に異常があるときの、RGBデータの再配分を計算する部分に極めて大雑把な近似をおこなっているので、その部分でも誤差が大きいと思う。

また、Red,Green,Blueの三色により色空間を形成しているため、各点を頂点とする三角形内に色空間は収まることになる。

計算ノート(Mathematica)はこんな感じである。

この計算結果を眺めながら、岡島修氏の「レーザポインタと色覚異常」中に記述されている色弱における混同しやすい色の例、

• 第1色盲
• 赤と黒
• ピンクと青
• 第2色盲
• 赤と緑
• オレンジと黄緑
• 緑と茶
• 青と紫
• ピンクと白
• 緑と灰色

というものを比較すると、割に納得できるのではないだろうか?

例えば、通常の色空間において赤(すなわち右上)の場所を第1色盲の色空間の中で見て欲しい。黒との識別が困難なのは一目瞭然だろう。また、下の図に示すように、通常の色空間でピンク(1)と青(2)が第1色盲の色空間の中でどうなっているかを見れば、

通常と第1異常の色空間におけるピンク(1)と青(2)

通常の色空間

第1異常の色空間

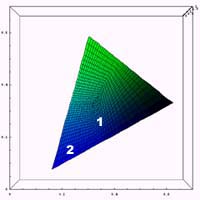これも1と2の識別が困難であることが容易に想像がつく。第2色盲でも同じように見てみて確認して欲しい。

なお、上の図中で中心部が暗くなっているが、それはグリッド線のためであり、本来の色はもっと白っぽい色である。また、今回は岡島修氏の「レーザポインタと色覚異常」中の図と比較するために、CIExy色度図を用いたが、もともとxy色度図は人間の感じ方とは結びつけにくい。いずれ、均等色空間における解析を行うつもりである。また、先に記述したようにきちんと錐体の波長感度特性を考慮に入れた計算をするつもりである。今回はあくまでごく簡単な実験である。

　というわけで、今回は色弱の方がどのような色空間を感じているかを考察してみた。今回の話中には色々間違いもあると思う。なにか訂正すべき情報を見つけてくださったら、教えて欲しい。

画像出力に携わる方でこのWEBをご覧になっている人もいるはずだ。色を正しく伝えることを日夜考えている人もいるだろう。しかし、色を正しく伝えることを考えるときに、考え忘れていることはないだろうか?　「正しい伝え方」は、誰にとって「正しい」のだろうか?私達が当然のように感じている色についても、異なる感じ方をする人のことを考え忘れてはいないだろうか?
　そういった人は少数だと言われる方もいるかもしれない。しかし、あなたが当然の権利のように享受しているものは果たして全ての人が得ているものだろうか?　もしかしたら、その権利を享受している人の方が少数派であるものもあるのではないだろうか?

　やることは至極簡単なことだ。技術的に言うならば、人の知覚も「デバイスの一部」として考えた際に、「人の知覚」が数種類あるものとして、異なるデバイス間のカラーマッチングを考えれば良いだけのことだ。もちろん、一筋縄ではいかないだろうが、得られるものの大きさからしたら、やってみる価値はあるだろう。

　プレゼンテーションソフト、あるいは数多くのソフトウェアにそういったことをきちんと考えたテンプレートが現れ、WEBサイトの色、画像機器のカラーマネジメントにそういった「全ての人(健常者と呼ばれる人のモデルだけでない)の感じ方まで含めたカラーマッチング」が適用されていく日も必ず来るはずだ。もしかしたら、このWEBサイトに来ている人の中には、今すぐにでもそういうことを始めることが出来る人もいるかと思う。果たして、そんなことが「できるかな?」と思われる人もいるかもしれないが、きっとできる筈だ。

　こういったことは色覚に限る話ではないと思う。考え忘れていることは数多くある。できることも数多くある、と私は思う。

■色空間の世界へ　 (色弱と色空間 その3)　

Someday

　今回は、
色を伝える時に、考え忘れていたこと(色弱と色空間 その1) - We can work it out! - (1999.08.09)
で行った計算を少し改良し、なおかつ色空間の世界を自由自在に動かしてみたいと思う。今回のメインは「立体グリグリ」のテストである。

まずは、前回と今回の計算の違いは、

• 前回はL,M,Sの各錐体の波長感度特性はRed,Green,Blueの単波長であるという仮定の元の計算
• 今回はL,M,Sの各錐体の波長感度特性はRed,Green,Blueの単波長とは異なるという条件での計算

ということである。計算式は、前回の

• Ｘ＝ 0.412391R + 0.357584G + 0.180481B
• Ｙ＝ 0.212639R + 0.715169G + 0.072192B
• Ｚ＝ 0.019331R + 0.119195G + 0.950532B

に

• l = 0.16*X + 0.54*Y - 0.033*Z
• m = -0.16*X + 0.46*Y+0.033*Z
• s = Z

を組み合わせている(何か堂堂巡りのような感じもする?...)。計算としてはおかしいところもあるが、とりあえず、今回は色空間をグリグリ動かして実感することが目的なので、(計算がチャチなのは)勘弁して欲しい。

　それでは、通常のRGB色空間と第1色盲(赤色盲)のRGB色空間を以下に示してみる。今回はMathematicaの出力をJavaAppletで動かすことができるLiveGraphics3Dを使用している。そのため、RGB色空間をグリグリ動かすことができる。それどころか、ステレオ画像にしてグリグリ動かすこともできる。ステレオ画像の見方は交差法である。ぜひ、試してもらいたい。

　下のグラフの操作方法は

• 操作 = 作用
• マウス左ボタンドラッグ = 回転
• シフトキー + 垂直ドラッグ = ズームイン・アウト
• シフトキー + 水平ドラッグ = 垂直軸についての回転
• コントロールキー + 垂直ドラッグ = 焦点距離の変更
• マウス右ボタン垂直ドラッグ = 部品除去
• "s"キー = ステレオ画像作成

である。詳しくは
PageLiveGraphics3D
( http://www.nikonet.or.jp/spring/sanae/LiveGraphic3D/LiveGraphic3D.htm)
を参考にして欲しい。それでは、RGB色空間(ハリボテバージョン)を自由自在に動かしてみよう。

通常のRGB色空間

第1色盲(赤色盲)のRGB色空間

　どうだろうか?　RGB色空間を自由自在に動かせただろうか?　立体グリグリはできただろうか? 「ハリボテでつまらない」なんていう文句がある人もいるかもしれないが、気が向けば立方体の全面について描画を行うよう変更するつもりである。

　こういった、Javaなどを使用した立体表現は表現力が非常に高い。しかし、読み手によっては必ず見れるとは限らないところが難しいところである。読み手を限定してしまう可能性が有る。それは、まさに色覚異常に関する問題と同じである。

　TVが白黒放送からカラー放送に移行する当時は、カラー放送においても白黒TVでもきちんと識別できる色を考慮しながら放送しようとしていた、と聞く。白黒TVで観ている人が困らないようにである。しかし、現在はどうだろうか? 白黒TVで観ている人のことを考慮したTVなどほとんど無いのではないのではないか?　

　TV放送に限らずWEB、プレゼンテーションなどにおいて、最新の可能性と広い互換性を両立させていくためには、他の人を配慮する力が必要だと思う。そういう点においても非常に優れ、私がとても好きなWEBサイトが今日から一時停止してしまった。非常にさみしい。

　それでは、今回の色空間自由自在はこんな所で終わりにしたい。

■立体音感を考える　

バーチャルサウンドソフトウェアを作ってみよう

　立体感というものには何故か強く心惹かれるものがある。まして、それが人工的な立体感であるならば、なおさらである。それは、画像・映像であっても、音であっても同じだ。色覚なども同様なのだが、人間の感覚というものを人間自身の技術により再現できたりするのが、実に面白い。

　何より、自分が実感できるというのが良い。結果を自分で感じることができるというのは、素晴らしいと思う。よくソフト技術者などで、「もう少し目に見えるものが作りたい」という人がいるが、それと同じである。

　小・中学校などでも実感できる教材や授業というのがあれば素晴らしいと思う。最近のWEBを眺めていると、そういう先生方のグループも多いようだ。そういう先生は「えらいなぁ」とつくづく思う。今の学校の先生は、そういうことをすればするほど、仕事としては時間単価が下がってしまうのだろう。それでも、そういった先生方は、きっとそういうことは気にしてはいられないのだろう。ホントにエライ。

　さて、立体感を実現するソフトであるが、そういった技術には色々なモノがある。音響の立体感の実現を目指す技術に関しても、古くから数多い技術がある。そういったものを追求しているWEBも多々あり、
　「今日の必ずトクする一言(http://www.tomoya.com/)」の

• 山本式スーパーバイノーラルコンペンセーターのナゾ(その２、ソースを考える編)
• http://www.bekkoame.ne.jp/~jh6bha/higa9810.html#981013
• 山本式スーパーバイノーラルコンペンセーターのナゾ
• http://www.bekkoame.ne.jp/~jh6bha/higa9810.html#981008
• 山本式バーチャルサウンドシステムのナゾその２(原理解説編)
• http://www.bekkoame.ne.jp/~jh6bha/higa9804.html#980421
• 山本式バーチャルサウンドシステム(PATPEND.)のナゾ
• http://www.bekkoame.ne.jp/~jh6bha/higa9803.html#980307

　などはその最たるものである。ここのWEBマスターなどは聴覚の専門家でもあるので、こういう話題に惹かれるのは当然なのだろう。

　また、そういったものを実現しようとする製品は昔から掃いて捨てるほどある。最近の製品では、

• ヤマハ、スピーカー間隔0でステレオ音場を実現するLSI
• http://www.watch.impress.co.jp/pc/docs/article/990122/yamaha.htm
• ヤマハ デジタルオーディオ用LSI『YSS901』
• http://www.yamaha.co.jp/news/99012101.html

などもそうである。(といっても、今回の話しはずいぶんと長い間塩漬けになっていたので、それほど最近ではなくなってしまったのが残念である。)

　私も出張などで新幹線などに乗っている際には、E-500などでヘッドホンで音楽を聴いていることが多い。そういう時には、先の「山本式スーパーバイノーラルコンペンセーター」などが欲しくなり、音の立体感などについて色々と考えてしまう。必要に迫られているせいか、立体音感については、私もとても興味を惹かれるのである。
　というわけで、「できるかな?」でも立体音響について考えてみたいと思う。といっても、考えるだけでは面白くない。それに「ナントカの考え休むに至り」ともいう。私が考えるだけでは、何にもならないし、しょうがない。色々と実験をして遊んでみたい。
　そのために、まずはいくつかの道具を作ってみることにした。

　今回、作成するのは、山本式バーチャルサウンドシステムソフトウェア(名付けてYVSSS。略称が長いので、以降YVS3と称することにする。)である。先の「今日の必ずトクする一言(http://www.tomoya.com/)」の一連の話しに出てくるそれである。スピーカーマトリックスの程度を小さくしたものである。

　バーチャルサウンドシステムソフトウェアというと仰々しいし、ものすごいソフトウェアに思えるかもしれないが、実はそんな大したモノではない。それどころか、実に簡単なモノである。実際には、Waveファイルを開いて、そのファイルの左チャンネル(L)、右チャンネル(R)に対して、

• R'＝ R - 1/3L
• L'＝ L - 1/3R

という処理をしてやるだけである。これが、どのような作用を持つか考えるのは、先に挙げた「山本式バーチャルサウンドシステム」のWEBを読めばわかるだろう。もちろん、本「できるかな?」的にも色々考えてみたいわけではあるが、それは次回以降に後回しである。今回は、YVS3を作成し、自分の耳でその効果を実感するだけである。

　ここに、今回作成したソフトを置いておく。いつものことであるが、完成度はアルファ版以下である。

• wavemixpro.lzh 444kB

　使い方を示しておく。まず、下が動作画面である。水平方向にスライダーがあるが、チャンネル同士の演算の係数を決めるものである。左端が0%であり、右端が100%である。

WaveMixPro(YVS3)の動作画面

　すなわち、スライダーが左端であれば、

• R'＝ R - 0 L = R
• L'＝ L- 0 R = L

となる。つまり、オリジナルそのままである。また、スライダーが右端であれば、

• R'＝ R - L
• L'＝ L- R

となる。差分を出力することになるわけだ。
　Load_Convertボタンを押して、WAVファイルを選択し、変換することができる。その際、オリジナルのファイルは"*.org"という名前で保存される。

　　さて、このソフトを使って、

• 種ともこのアルバム「感傷」から「はい、チーズ!」
• THE POLICEのLive at the "Omni" Atlanta, Georgia During 1983 U.S.A Tourから"SoLonely"

を試聴してみた。「はい、チーズ!」は途中がLive録音であるし、"So Lonely"の方は完全にLive録音であるからだ。

　試聴のやりかたは、Cd2wav32.exeを使い、CDからWAVファイルにする。そして、WaveMixPro(YVS3)を使って、バーチャルサウンドシステム構築する。そして、それをヘッドホーンで試聴するわけだ。適当にチャンネル同士の演算の係数を変化させ、聴いてみた。果たして、立体感は増しているか?

　さて、試聴した結果であるが、「うーん。」という感じだ。
　係数を大きくすると、まるで「カラオケ製造器」である。ボーカルが消えるだけである。しかも、聴衆が頭の真ん中に居座っているような感じである。つまり、立体感がむしろなくなってしまっている。「何故、オマエらはオレの頭の真ん中で拍手をするのだ」、と言いたくなる。頭が変になりそうである。
　かといって、小さいとよく違いがわからない。困ったものである。

　さてさて、まだまだ第一回目ではあるが、前途多難の気配であるのが心配なところだ。

■色覚モドキソフトを作る(色弱と色空間その4)　

五十歩百歩

　　まず、先に書いておこう。今回は、

• WEBページは会社の心(色弱と色空間 その2) - WEBページのカラーを考える 3 - (1999.08.10)

で作成したTrueColorと似たようなプログラムを作成してみたい。何しろ関係ない話が以降、長々と続くからである。

　 昔から、科学者は「色」というキーワードに強く惹かれている、と思う。そんなことを私が思うまでもなく、量子色力学(quatumchromodynamics)、色つき空間群(Color-symmetry)等のキーワードにその事実は現れている。これらの言葉は普通に使われる「色」という言葉とは違う性質を表すものである。しかし、科学者が「色」というものを基本的なものであると感じているために、どんなものが対象でも、「性質」の代表的なものとして、「色」という言葉が連想されるのだろう。

　 私は学生時代の量子力学の授業のおかげで、「色」という言葉を聞くと今でも眠くなってしまうのである。何しろ、私の通う理学部の教室の横は農学部の畑だったのだ。教授の声と共に「モゥーーー」という牛の鳴き声が聞こえてくるのだ。教授の声と牛の鳴き声が絶妙のハーモニーとなるのである。ただでさえ眠くなるのに、そのハーモニーはクロロホルムもビックリの睡眠作用を発揮するのだ。私はそのハーモニーのおかげで何回も記憶を飛ばされた。
また、その牛達のおかげで、授業の中で「匂い」と聞いたりすると、牛の糞の「匂い」しか連想できないのである。困ったものである。あの農学部の畑がなければ、もしかしたら私は量子力学を好きになっていたかもしれない。そして、量子力学を極めていたかもしれないのだ...簡単に言えば私は量子力学の授業では落ちこぼれてしまったわけだ。

　 ところで、昔の科学者達を考えると、「色」に関わらなかった人を探すほうが逆に難しいように思う。ニュートン、マクスウェル、ヤング、ヘルムホルツなどが代表的である。当たり前である。物理・化学に関わらず、「光」には関わらざるを得ない。当たり前である。さまざまな計測を行ったり、エネルギーを考えたりする上で光は最も重要なモノである。
　そして、「色」というものは「光」の大きな性質の一つである。しかも、それは「科学者自身にとっても」目に見える性質である。目に見えるものを無視する科学者は少ないと思われるので、科学者が「色」に関わらないわけにはいかないのだ。

　 割に最近の科学者でも、意外な分野の人が「色そのもの」の研究をしていることがある。例えば、シュレディンガーなども色空間の提唱をしていたらしい。確かに、量子力学から色空間へはつながりを感じないこともないのではあるが、少し意外でもある。そのシュレディンガーが提唱した色空間がどのようなものであるのか、私は残念ながら知らないのだが、波動を深く研究していたシュレディンガーが提唱する色空間というのは非常に興味のあるところである。また、化学。物理学者であるダルトンは自らも色弱であるため、特にその辺りのことを研究し、報告している。

　　さて、そのダルトンをinfoseekで検索してみると、

• ダルトンレンズ　(http://www2u.biglobe.ne.jp/~ohsaka/index2.html )

というページを見かけた。ここに、色覚バランスチェック用の図があった。昔、身体検査でやったことがあるような図である。こういった、図が人によってどのように見えるかは非常に興味があるし、気にかかるところでもある。
　もちろん、WEBページは会社の心(色弱と色空間 その2) - WEBページのカラーを考える 3 - (1999.08.10)で作成したTrueColorも同じような目的のために作成したものであるが、あれはあまりにも大雑把なモノだったので、作り直してみたいのである。なお、今回は画像のRGBとL、M、S錐体の反応の間の変換は

画像のRGBとL、M、S錐体の反応の間の変換マトリクス
左=RGB2LMS、右=LMS2RGB

という変換マトリクスを用いている。

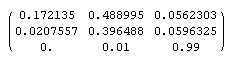　　そこで、こういったWEB上の画像を読み込んで、

• 目に映る明るさって何ですか?- 君は天然色 - (1999.07.05) 　

でやったL,M,Sの各錐体の感度が低いときの色覚シミュレーションを行うソフトを作成してみた。ソフトはこれである。

• truecolor2.lzh ( 247kB)

前回と同じく、Susieプラグインを用いて画像を読み込んでいるので、「Susieの部屋」などから、Susie本体・あるいはプラグインを入手する必要がある。
　また、手間を惜しんだためProxy対応にはしていない。さて、動作画面サンプルを以下に示す。初期状態では

• ダルトンレンズ　(http://www2u.biglobe.ne.jp/~ohsaka/index2.html )

から画像を読み込むようになっている。もちろん、他のURLからも画像を読み込むことが可能である。画面左の三本のスライダーで各錐体の感度を調整できる。

truecolor2.exeを実行した画面

　　この画面例では各錐体の感度は全て100%になっている。

　　それでは、以下に適当に錐体の感度パラメータを変化させた場合のサンプルを示してみる。

truecolor2.exeで錐体の感度パラメータを変化させた場合のサンプル

　　こうしてみると、これまで見てきたものとは違う数字が浮かび上がることがわかる。89,52などである。こういう仕組みを用いたのが、石原式などの色覚検査のやり方である。つまりは、異なる色を識別できないこと、すなわち、混同色を用いているのである。混同色を用いて文字を描くことにより、色弱であるかどうかを判断しようとするものだ。

　　さて、こういった書き方をすると、色を混同してしまうのが色弱の人だけと勘違いされてしまいそうであるが、そんなことはない。全ての人が「色を混同してしまう」のである。どんな人でも、異なる波長の光であっても、例えばRGBなどの(多くても)三色を混合すれば同じ色に見えてしまう。つまりは、混同色だらけなのである。健常者と呼ばれるヒトも色弱と呼ばれるヒトもたかだか数種類の錐体を持つにすぎない。
　色々な光の波長分布を認識できる生物がいたとすると、彼らがからすればヒトは全て色弱ということになるのだろう。つまりは、五十歩百歩といったところなのかな、と思うのである。