2000-02-19[n年前へ]
■携帯電話の同時性? 
競馬の写真判定とパノラマ写真 その後
先日
を書いてから面白いメールを頂いた。その一部を抜粋すると、小生は超音波を利用した新しい流体場測定を行っていますが、この方法で得られるDataは空間1次元時間1次元の2次元データです。従って得られるのは、このページにあったような画像が直接得られるわけです。とある。この方法といくつかの結果を発表してから、あちこちからコンタクトがありましたが、その中の一つが、NYのSirovichという高名な流体力学者からの手紙でした。彼はいわゆるSnapShotを、逆に小生のデータから構築できないか、というのです。
今このWebでされたことの逆をしたいというわけです。流れの空間構造を解析するために使いたいのです。残念ながらこれは、以下に少々説明するように、原理的に無理な話で断らざるをえませんでした。
つまり、時間軸に速度をかけて空間軸に変換できればよいのですが、流体場はそれ自身が速度分布を持っていますから、一体何を使えば良いのかが定まらない。
電磁波の場合には光速が一定ですから、時間情報から空間情報を得ることができますが、古典流体力学では不可能なのです。工学的には平均流速を使って、時間-空間の変換をしますが、それはインチキとまでは言わないまでも、便宜的なも
のでしかありません。このWEBの中での例では、馬?の速度のみであとは静止しているので、可能でし
ょう。
「馬?」という箇所に、私との意見の相違があるようだ。私が明らかに「馬」であると言い張っているものに疑問を持たれているような気がするのであるが、今回そこは気にしないでおく。
なるほど、音波や電磁波などを使って計測を行い、得られた
- 空間(あるいは量)-時間
- 空間(あるいは量)-空間
- 海の中の魚を探知する「魚群探知機」
- 気象状況を計測する「気象レーダー」
- 固体の中の電荷分布を計測する「電荷分布測定装置」
「魚群探知機」は超音波を水中に発信して、その反射波が刻々と帰ってくる様子から、(超音波の速度を用いて、空間位置に変換した後に)障害物(ここでは魚群)の様子を計測するものである。「気象レーダー」も電波を使って同様に雲の分布などを測定する。
「電荷分布測定装置」の場合は、(例えば外部電界を印加し)電荷を持つ個所を振動させてやり、その振動がセンサー部に刻々と伝わってくる様子から(あぁ、なんて大雑把な説明なんだ)、(固体中の弾性波の速度を用いて、空間位置に変換した後に)固体の中にどのように電荷分布が存在しているかを計測するものである。
と、文章だけでは何なので、WEB上から、それらの計測器を用いた場合の計測例を示してみる。
下が魚群探知機である。リンク先は
である。 |
また、この下は空間電荷測定装置である。これなども、とても面白いものだ。リンク先は
である。 |
さて、こういうことを、調べてみるだけではしょうがない。自分でもそういう計測をしてみたい。
そこで、次のような実験をしてみようとした。
- 部屋の中に複数の「音の発信源」を配置する。
- 複数の「音の発信源」から同時に音を発する。
- それをPCで収録する。
- 音声が「音の発信源」からPCに到達するまでの時間を解析する
- 複数の「音の発信源」の位置を計測する。
そこで、安易にも時報を使おうかと考えてしまった。しかも、数があって手軽ということで、携帯電話を使おうとしたのである。
しかし、複数の携帯電話を集めて、117に電話して時報を同時に聞いてみると、とても同時どころではない。てんでばらばらなのである。電話のスピーカーから流れてくる時報のタイミングには結構ズレがあるのである。
携帯電話の間には結構同時性がないのだ。また、固定電話とも比較したが、固定電話よりも時報が速いものもあれば、遅いものもあった。
そこで、複数の携帯電話を聞き比べた結果を以下に示してみたい。この写真中で左の携帯電話ほど時報が先に流れており、右になるほど時報が遅れているのである。一番早い左と、一番遅い右では一秒弱の違いがあった。
 |
また、参考までに、家の固定電話と携帯電話の時報を一緒に聞いたサウンドファイルを示しておく。
この携帯電話は先に示した画像の一番左である。つまり、先の携帯電話群では一番時報が早かったものなのである。しかし、家の電話よりは一秒弱遅かった。ということは、家の固定電話と先の一番遅い携帯電話では時報の時間にして2秒弱の違いがあることになる。 そして、「家の固定電話と携帯電話の時報を一緒に聞いた音の変化」をスペクトログラムにしたものを以下に示す。
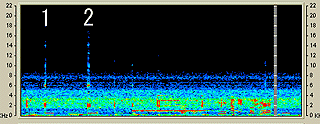 |
水平軸が時間軸であり、時間は左から右へ流れている。また、縦軸は音の周波数を示している。ここでは、「1」で示したのが家の固定電話の時報であり、少し遅れて「2」の携帯電話の時報が聞こえているのが見てとれる。
よく時報を確認することはあるが(実は私はほとんどないのだが...)、携帯電話・PHSで時報を聞く限り、秒の精度はそれほどないようである。また、勤務先の固定電話は先の携帯電話群と比べても遅い方であった。それは少し意外な結果であった。
今回調べた「携帯電話の同時性のなさは」は常識なのかもしれないが、電話の時報で時計を合わせるのはあまり精度が出ないやり方であることがわかっただけでもよしとしよう(別に実験を途中で投げ出した言い訳ではないけれど)。
今度、TV(衛星TVなども遅延時間を考慮した時報の放送を行っていると聞くし)やラジオを用いて当初計画していた実験を行おうと思う。その際には、時報がPCに到達する時間のズレで「音の発信源」までの距離を計測し、左右のマイクでの違いを計測することにより、「立体音感シリーズ」のように「音の方向」を得てみたい。
というわけで、話が「立体音感シリーズ」に繋がったところで、今回は終わりにしようと思う。
2000-08-16[n年前へ]
■エアコンの風は心地よく吹くか? 
真夏の夜の夢 流体力学入門編
私は長野県の野辺山という高原で幼い時期を過ごしたせいか、暑さにとても弱い体である。なので、真夏の夜はエアコンが欠かせない体と根性になってしまった。エアコン無しではろくな夢が見られ無いどころか、眠れなかったりするのである。気持ちの良い「真夏の夜の夢」を見るためには、エアコンがとっても重要なのである。
つい先日、そんなエアコンの話題が「今日の必ずトクする一言」に載っていた。それが、
- エアコン用流体素子(PATPEND.)のナゾ
- ( http://www.bekkoame.ne.jp/~jh6bha/higawari.html#000819 )
- 復活する冷蔵庫脱臭剤のナゾ(1/f揺らぎと活性炭編)
- ( http://www.bekkoame.ne.jp/~jh6bha/higawari.html#000901)
(おそらくhiraxさんあたりがやってくれるのではなかろうか)と話題のパスまでされている。いきなり、ボーとしているところを授業で当てられた気分である。
とはいえ、「エアコンの流体力学」というのもちょっと興味のある話題でもあるし、パスされたからにはやってみなければなるまい。そういうわけで、真夏の眠れない夜のパズル代わりに挑戦してみることにした。
さて、部屋の中の「エアコンから送られる風の様子」を計算するということは、流体力学の計算をするということになる。流体力学の運動方程式(ナビエ・ストークス式)に代表されるような方程式群を解かなければならないのである。そこで、以前
の時にいじりかけたMichael Griebel氏らによる非圧縮性流体のNast2Dのコードをもう一度引っ張り出して使ってみることにした。このNast2Dは非圧縮性二次元流れを計算する教育用のソースコードである。詳しくは- TUM INFO V- Homepage - ( http://www5.informatik.tu-muenchen.de/home_us.html )
- Numerical Simulation in Fluid Dynamics A Practical IntroductionISBN 0-89871-398-6
計算するモデルは次の図に示すような部屋である。四畳半一間であるかもしれないし、100畳以上の大きな広間かもしれないが、とにかく正方形の部屋だ。向かって左の青い丸部分にはエアコンがあり、そこから冷たい空気が送られてくるのである。そして、この部屋には何故かタンスがおいてある。「やっぱり、この部屋は四畳半一間じゃないの」というツッコミは言ってはいけない約束である。とりあえず、このタンスが向かって下側にある紫の部分である。このタンスが、エアコンから送られてくる冷た〜い空気流の障害物となるのである。
 |
暑い真夏の夜に、こんな部屋をエアコンで涼しくする時のことを考えてみよう。気持ちよく眠るために、何はともあれエアコンのスイッチを入れるわけだ。そうしないと、暑くて眠れないから当然である。
そして、そのエアコンには送風モードが何故か三つあるのだ。次のような三種類の送風、
- 真っ直ぐ送風するモード
- 単純な首振り送風をするモード
- 山本式エアコン用流体素子を用いた送風をするモード
空気流の速度分布の計算結果を次に示してみよう。
|
| を用いた送風の場合  |
また、これらの場合の計算結果を動画で示したものをMPEG4形式のAVIファイルとReal形式のファイルにしたものを以下に置いておく。エアコンから空気が送られる様子を知るには、何はともあれこの動画を見て頂きたい。なお、手元のRealProducerの制限のために、このReal形式のファイルは古いバージョンのRealPlayerだとアップデートが必要になってしまった。また、MPEG4のCodecが導入されていない場合には、DivXなどをインストールする必要がある。
とりあえず
- 真っ直ぐ送風している場合 MPEG4 AVI ( 289KB ) Real形式( 73KB )
- 単純な首振り送風の場合 MPEG4 AVI ( 577KB ) Real形式( 89KB )
- 山本式エアコン用流体素子を用いた送風の場合 MPEG4 AVI( 693KB ) Real形式 ( 92KB )
また、それぞれのMPEG4形式の動画のファイルサイズを見れば、それぞれの場合の送風による空気流の速度分布の複雑さは一目瞭然である、と思う。真っ直ぐ送風している場合はとにかく単純な速度分布であって動画ファイルサイズも結果的に小さくなっているのに対して、山本式エアコン用流体素子を用いた送風の場合はかなり複雑な速度分布になっていて動画ファイルも結果的に大きくなっているのである。
動画を見ることができない人のために、それぞれの場合の連続した3つの瞬間における部屋内の空気流の速度分布の静止画も示しておく。
1 | 1 | を用いた送風の場合 1  |
 |  |  |
 |  |  |
これを見ると、「真っ直ぐ送風している場合」にはエアコンの正面は強烈に風が当たっている(つまり冷えまくっている)ことがわかるが、タンスの陰になっている部屋の隅などはほとんど空気が動いていないことがわかる。また、「単純な首振り送風の場合」は送風方向を動かしているとはいえ、その送風方向の変化はかなりゆっくりであって部屋の中の空気流の速度分布はそれほど急激には変化していないことも判ると思う(そういう風に計算しただけではあるが...)。いずれにせよ、もしもこの部屋の中にあなたがいたとしたら、体の決まった部分にのみ冷た〜い風があたることになるわけだ。それは体にはちょっとよろしくなさそうである。
一方、「山本式エアコン用流体素子を用いた送風の場合」は時々刻々と送風方向が変化しており、まるで部屋を舐め回すかのように、冷た〜い空気が送られていることがわかると思う。この部屋の中にもしあなたがいたとしても、体のごく一部分だけに冷たい風が当たるようなことはなく、それほど体に悪くないことが予想されるわけである。
さて、このページもかなり重いページになってきた。本来はこのタンスの裏側の空気が澱みやすい場所の「空気の入れ替わり」を、送風の具合を変えた上で調べてみたいわけであるが、それは次回のお楽しみ、ということにしておきたい。とりあえず、「真夏の夜の夢 流体力学入門編」はここら辺で終わりにしたい。
さて、夏休というわけでこんな景色のところで気持ちの良い風に吹かれてみたりするわけである。この写真の先の方の海の向こうに見えているのは左が伊豆半島で、右が三保の松原の辺である。

暑い夏の夜はエアコンが欠かせない体ではあるけれど、気持ちの上で言えばエアコンよりはおんぼろの扇風機の方が好きだし、扇風機よりも山の上の風の方がずっと好きだ。いつか、山の上を吹き抜ける風の音を録音して、その1/f揺らぎでも調べてみようかなと思うのである... それとも、そんなことをしてもツマラナイだけかな?
2000-08-24[n年前へ]
■スクール水着の秘密 
腹の部分のデカイ穴 流体力学入門編2
先日、「とあること」を知って、とてもビックリした。とてもびっくりしたあまり、「男と女の人の間には知らないことがいっぱいあって、そこには深くて暗〜い河が流れているんだなぁ。」とシミジミと考え込んでしまったくらいである。いや、誇張でなくて本当にそう思ったのである。
今回出てくる話を私のように知らない人がいたならば、もしそれが男性であれば私のようにビックリして哲学的なことを考えてしまうだろう。そして、それがもしも女性であれば「自分が常識だと思っていたささいなこと」を知った男性が「どれほど驚愕するか」を知れば、やはり同じようにビックリするに違いない。私はこの「とあることから始まる真夏の哲学をぜひ多数の人に知って頂きたい」と思い、筆をとることにした次第である。
一体、その「とあること」が何かと言うと、それは「女の子のスクール水着のお腹部分は実はセパレートになっていて、大きな穴が開いている」ということである。一応、簡単な絵を示しておこう。
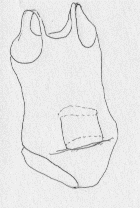 |
といっても、私が詳しく知っているわけはないので、もっと詳しいことは、
- スクール水着の謎 ( http://tako.2ch.net/test/read.cgi?bbs=entrance&key=964275735 )
- 一般的なスクール水着のしくみについてのご説明 (http://kanna.piko.ne.jp/page-L/picture.LLL.htm )
何故、そこに「スクール水着の謎」の中で、
あそこの部分は”前垂れ(まえだれ)”って言うんだよ 。あのね、あの前垂れはね、泳いでいる時に胸の谷間から入った水を泳いでいる方向から観て後方に 排出する為に有るの、あれが無いと胸の谷間から入った水が水着の中に溜まっちゃうのよ。 だから簡単に言うと前垂れは、排水口みたいな物なの。という風に簡潔に説明されている。そう言われてみれば、そういうものなのかもしれない。しかし、ビックリである。ちょっと本当に驚いて、そして少し感動までしてしまった私は「スクール水着の前垂れ部分の水流の様子」を今回解析してみることにしたのである。
まずは、こんな感じで泳いでいる女性がいたとしよう。
 |
この画像では水着が見えないかもしれないが、この女性は当然水着を着ている。「心の清らかな人」にはちゃんと水着が見えるハズである。「邪な心の人」には水着が見えないかもしれないが、それは心に煩悩を抱えているせいである。ぜひ、悔い改めて欲しいと思う。まして、「コイツPoserの使い方が判らないんだろう?」などという言うような輩(ヤカラ)はもってのほかだ。
さて、この下の画像のように女性の胸の辺りの水流を解析してみることにしよう。注目する領域はすなわち赤い線で囲んだ部分である。
 |
上の画像で胸を消してあることが判るだろう。それは今回の解析は胸の谷間から水着の中に入っていく水流の解析をする、つまり胴体の中央部での水流の解析をするからである。胴体の中央部にバストがついている女性はそうそういないだろう。
さて、その部分の拡大図を次に示そう。スクール水着に前垂れがなくて、水着の中に入った水の逃げ場がない場合、次の図のような感じで胸と水着の間にスペースができてしまう。
 |
一方、スクール水着に前垂れがあって、水着の中に入った水の逃げ場がある場合、次の図のようになる。胸と水着の間にスペースができることは同じであるが、そのスペースから水が排出されていく経路があるわけである。
 |
さて、今回の流体解析も
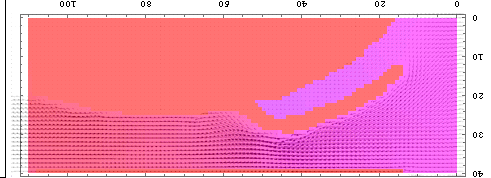
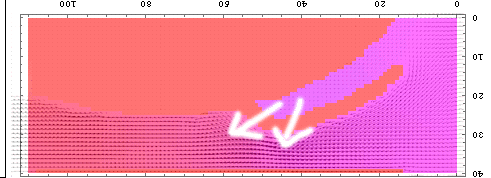
の時と同じく、Nast2Dを適当に改造して簡単に解析を行ってみた。今回はReynolds数は100で計算してみたが、次に計算するときにはReynolds数の妥当な値を考慮してやってみたいと思う。残念ながら、今回は本当に適当に計算をしてみただけである。まぁ、最初の試しだからそんなものだ。 まずは「前垂れがなくて、水着の中に入った水の逃げ場がない場合」の水流の速度分布の計算結果を下に示してみよう。
 |
胸の谷間に水がたまったスペースの後ろ部分の水流がずいぶんと速くなっていることがわかるだろう。当然のごとく、胸の谷間に水がたまった部分では水は滞留してしまっている。
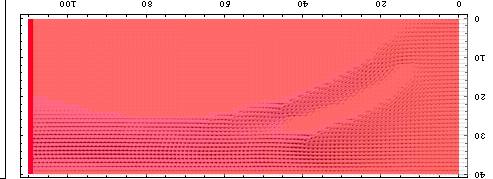
一方、「前垂れがあって、水着の中に入った水の逃げ場がある場合」が次の図である。
 |
胸の谷間を水がジェット気流のように速く抜けていくことがわかる。割にどの領域でも、水流の速度分布は割に等しくなっている。
次に圧力分布と水流の速度分布を重ねてみたものを示してみよう。まずは、「前垂れがなくて、水着の中に入った水の逃げ場がない場合」である。
 |
胸の谷間に水がたまっている部分は圧力が高いが、その外側の部分は圧力が低くなっていることがわかるだろう。
この圧力差により、次の図のような力が働いてしまう。
 |
こんな力が働いてしまうと、速く泳ぐ邪魔にもなってしまう。また、この力が大きくなると水着の締め付ける力を上回ってしまうだろうから、ますます水がたまるスペースが大きくなったり(つまり胸のスペースが広がってしまったり)、さらには水着を脱がす方向に働いてしまうことだろう(それはそれで良いぞ、という声も聞こえてきそうであるが)。
一方、「前垂れがあって、水着の中に入った水の逃げ場がある場合」は次の図のような感じである。
 |
圧力の不均衡もそんなに発生していないことが判るだろう。これなら速く泳ぐ邪魔にもならないし、水着もちゃんと体にフィットしたままである。
このように、スクール水着に隠された「前垂れ」は実に役に立っていることが流体解析からも判るわけだ。いやぁ、本当にビックリだ。
さて、私の周りの男性はやはりみな「スクール水着の秘密=前垂れ」を知らなかった。
「腹の部分にデカイ穴〜!? はぁ? スクール水着にそんなものあるわけないじゃないの。」とみな口を揃えて言うのである。もう、誰一人として素直に信じる人はいないのである。しかもこともあろうに、私をヘンタイ扱いまでするのである。いつの時代も真実を伝える者は受難の運命が待っているのである。実に嘆かわしいことである。
「オマエ、変な妄想でも見たんじゃないの〜」
しかし、それが「スクール水着の真実」を知ってしまった後は、どの人も
「えぇ〜!! 昔の俺達にそれを教えてやりたい〜!!」と驚きのあまり興奮してしまうのである。しかも、みんな
「誰一人としてそんなこと教えてくれなかったぞぉ〜」
「俺達の青春を返せ!って気分になるなぁ〜」
「もっと早く教えてくれよぉ〜」というニュアンスがアリアリと感じられるのである。さっきまで人をヘンタイ扱いしていたくせに、コロッと変わりすぎである。
しかし、女性陣はと言えば、
「あぁ〜そう言えば、そんな風になってたような〜。」と実に淡々としたものなのである。男心を全然判っていないのだ。その証拠に、
「あそこの穴から空気を入れて遊んだ〜。」
「えぇ〜、知らないのぉ〜」
「それにしても、何でそんなに驚くのか全然判りませ〜ん。」と言う人までいるのである。「そりゃ、驚くぞ」と男なら判るはずなのだが、それが女性にはどうも伝わらないのだ。
そういうわけで、「スクール水着の秘密」を通して私は「男と女の間の常識・意識のギャップ」を本当に真剣に考えさせられたのである。そのショックの余韻は今もまだ醒めやらぬままだが、とりあえず今回はここまでで終わりにしたい。
2000-10-29[n年前へ]
■「しょんべん小僧」の物理学 
あともう一歩、前に出ろ
以前、- スクール水着の秘密 - 腹の部分のデカイ穴 流体力学入門編2 - (2000.08.24)
「男性にはよくある風景だけれど、女性にとっては未知のミステリアスゾーン」といってもたくさんあると思うが「男子トイレ」というものだって、女性にとっては未知のミステリアスゾーンだろう。
次の絵はよくある男子トイレの一風景だ。便器前のポジションに立つとどうしても目に入る位置にこんな内容を書いたチラシが張ってあることが多い。
「ちょっと待て、あともう一歩前に出ろ。」
 |
もし、その張り紙がなかった場合にはどうなるだろうか?その場合には、下の絵のような事故が発生してしまうのである。実際のところ、ほとんどの公衆便所で見かける風景だ。
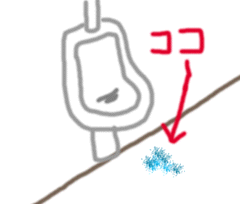 |
そう、便器にロックオンして放水をしたハズなのに、何故かターゲットである便器まで「小便」が届かずに便器下を汚してしまうのである。実にマズイ事態ではあるがよく見かける風景でもある。便器内を狙ったハズの小便が残念ながら目標地点まで辿り着かなかった場合に起きる悲劇である。
もちろん、どんなに飛距離が小さくても、すなわち小便が放水銃の先から真下に垂れてしまった場合でも、便器の顎の上から放水作業を行っていれば何の問題もないわけだ。しかし、世の中の男性達は何故か遠くから狙いたがるのである。先程の、「ちょっと待て、あともう一歩前に出ろ。」という張り紙ではないが、もう一歩前に出て便器の顎の上から放水作業を行いさえすれば良いのではあるが、何故か漢(ここではあえて、漢と書いてオトコと読むことにしよう)達はそれができないのである。
さて、この現象には別に公衆便所でなくても発生するわけで、どこのトイレでも便器の下を汚してしまうことになる。そのため、家庭によっては妻から
はるか古の昔から「男らしさ」のひとつが「立ち小便」でなかったか?、そして「立ち小便」は「男らしさ」の最後の砦ではないのか?という気も私は少しだけしたりするのだが、便器周りを汚しまくる現実の前ではそんな「男らしさ」は2000円札よりも価値がないのである。2000円札ならば喜んで受け取ってくれる人もいるだろうが、便器の下に落ちようとする「小便」は誰も受け取ってくれない。いや、実際のところ小便を喜んで受け取ってくれる人もいるのかもしれないが、少なくともそんな人の数は2000円札を喜んで受け取る人の数よりはきっと少ないだろうと思うのである。
そしてさらに、「男らしさ」が「立ち小便」なら、そんなものイラナイと言われてしまいそうな気もするし、「立ち小便」が「男らしさ」の最後の砦か!?と言われてしまいそうな気も強くするので、ここらへんについての社会学的な考察は追求しないでおこう。
それでも、私は世の中の虐げられている「しょんべん小僧」達のため、そして「男らしさ」の最後の砦を守るために、男子トイレの「しょんべん小僧」達がどうしたら、放水ミスをしないかを物理的に考えてみることにしたい、と思うのである。
さて、便器まで小便が届かないという「放水ミス」はどのようにすれば防ぐことができるだろうか?小便の飛距離を小さくしないためにはどのようにしたら良いだろうか?そのためには、まず小便の飛距離がどのようにして決まるのかを考えなければならないだろう。
下のちょっとリアルな「しょんべん小僧」の放水作業ではないが、小便の軌跡はきれいな放物線を描く。
 |
すなわち、空気抵抗などは無視した場合のピストルの弾と同じく
- 銃筒の先端を出るときの初速度
- 銃筒の角度
銃筒の先端を出るときの初速度 = V0と表すと、小便の飛距離は
銃筒の角度 =θ
a V0^2 Sin[2θ] (aは定数)と表される。この式を見ればθ = 1/2 rad.の時にSin[2θ]が1になるので一目瞭然であるし、また感覚的にも自然であるが、銃筒の角度の方は上向き45度の角度に向けるときに小便の飛距離は最大になる。一方、初速度V0の方は速ければ速いほど、小便の飛距離は伸びる。
それを示したのが、次の図である。「小便の銃筒の先端を出るときの初速度と銃筒の角度を変えた時の小便の飛距離」を示したものだ。
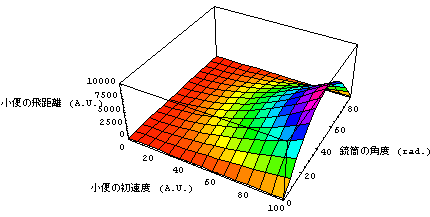 |
すると、便器まで小便が届かないという「放水ミス」すなわち、小便の飛距離を小さくしないためには、銃筒の角度を大きくしすぎたり、小さくしすぎたりしないという知見が得られるわけであるが、そんなことは当たり前だ。誰もトイレで銃筒を真上に向けたり、真下に向けたりはしないのである。先のちょっとリアルな「しょんべん小僧」ではないが、手で放水銃を支持している限り何の問題も無いのである。
つまり、便器まで小便が届かないという「放水ミス」はほとんどの場合「放水銃の角度」のせいではないのである。つまり、「銃筒の先端を出るときの初速度」が問題だったと考えるのが自然である。
それでは、「銃筒の先端を出るときの初速度」はどのようにして決まっているのだろうか?それを大雑把に考えてみたのが次の図である。腹筋で膀胱に圧力Pをかけて、銃筒の先端から小便を初速度V0で放水作業を行うのである。
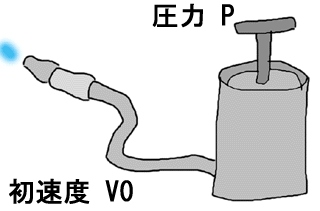 |
ところで、上の絵でポンプとして表した膀胱に圧力Pをかけた場合には、膀胱からb P (bは比例定数)と表せる量の小便が銃筒に送り込まれるものとしよう。その場合、その量の小便が銃筒の先端から単位時間に出るわけであるから、銃筒の先端の口径をAとすれば、
V0 = b P /Aと表すことができる。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのである。
さて、いくら腹筋が強い人であっても腹筋をいきなり締め付けることはできない。つまり、腹筋で膀胱を締め付ける圧力Pというものは徐々に大きくなるのである。
すると一見、「銃筒の先端を出るときの初速度V0」も0から徐々に大きくなる、すなわち、放水作業を開始した最初の瞬間は「銃筒の先端を出るときの初速度V0」= 0であって、小便の飛距離も0である、つまり、便器まで小便が届かないという「放水ミス」が必ず起きるかというと、実はそういうわけではない。
ポンプである膀胱から銃筒の先端までは、ある程度の長さがある。もちろん、その長さは一定ではないのだが、とにかくある程度の長さがある。そのため、小便が銃筒の先端から出る瞬間には、ポンプである膀胱にかかっている圧力Pは0ではないのである。すなわち、膀胱から銃筒の先端まである程度の長さがありさえすれば、「銃筒の先端を出るときの初速度V0」は結構大きくすることができるのだ。もちろん、腹筋を鍛えて、腹筋に急激に力を掛けることができれば、その効果はさらに上がることは言うまでもない。
だとしたら、一般的に便器まで小便が届かないという「放水ミス」は一体何時起きるのであろうか?それは、「銃筒の先端を出るときの初速度V0」を決める膀胱にかかる圧力Pが低下し、なおかつ最初の瞬間と違い「膀胱から銃筒の先端までの長さ」を有効に活用できない、放水作業を終える瞬間である。飛行機でも着陸が一番難しいというが、この放水作業もやはり放水作業を終える瞬間が一番難しいのである。そのため、多くの場合小便達は便器内への着陸に失敗し、便器の下を汚してしまうのである。
しかし、私は「男らしさ」の記念物でもある「立ちしょうべん」を守るために、一つの解決策を考えついたのである。「男らしさ」の最後の砦を守る技術を提唱したいのである。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのであるから、放水作業のラストに膀胱を締め付ける圧力Pが小さくなった、あるいは、膀胱を締め付ける圧力Pを有効に膀胱からの排水に変換できない排水作業のラストにおいて、銃筒の先端の口径Aを小さくしてやればよいのである。そうすれば、「銃筒の先端を出るときの初速度V0」は「銃筒の先端の口径A」に反比例するのであるから、膀胱から出てくる小便の量が低下しても、「銃筒の先端を出るときの初速度V0」を0にならないように維持することができるのである。これにより、放水ミスを防ぐことができるハズなのである。
さて、私は「男らしさ」の最後の砦である「立ちしょうべん」を守るために、このような技術を考えてみたわけであるが、この技術の実証作業は行っていない。果たして、「銃筒の先端の口径A」を自分の意識で小さくすることができるか!?というところに大きな問題点があるような気もするのであるが、それは「男の意地」で克服できると私は信じている。外部から制御するって手もあるのだし。って何の手の話だ、全く。
2001-01-23[n年前へ]
■今日の疑問 
次回の話は流体力学の話なのだが、某サイトでも同じく流体力学の話が出ていた。なかなかに面白い。ところで、粘性項を無視したポテンシャル流れで、最短距離の出口以外の所に先に着くのはちょっと不思議なのですけど、いかがなものでしょう? > webmaster殿

