hirax.net::Keywords::「無名関数」のブログ

■スペクトル処理で遊ぶためのMathematicaノートブック　

　色処理・スペクトル処理で遊ぶためのMathematicaノートブックを作ってみました(Mathematicaノートブック, PDF)。このノートブックはあくまで遊び用ですから、「できること」はとても限られています。けれど、Mathematica初級者が(Mathematicaの使い方を覚えながら)色処理・スペクトル処理を行おうとする時のスタート地点としてならば、少し役に立つかもしれません。例えば、plotSpector red なんてタイプすれば、右の画像中にあるようなカラフルなスペクトル・グラフが表示されたりします(右の例はシアンを表示したものですが)。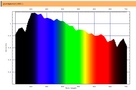また、rgb = fitSpector cyan, red, green, blue なんてタイプすれば、シアン色を(スペクトル分布を考慮した上で)RGBに分解できます。もちろん、fitSpector hogeColor, cyan, magenda, yellowなら、hogeColorをcyan,magenda,yellowというスペクトルで再構成できるわけです。あるいは、setcolor cyan ; {L, a, b} なんて入力すると、任意のスペクトルをLab色度座標を計算したりできる…という具合です。

　このノートブックの一つの特徴は、連続する「スペクトル」を(離散的なリスト)でなく「関数」として取り扱うところです。ですから、cyan467.34なんて入力すると、波長467.34nmでのシアンの光強度が出力されたりもします。そして、そんな関数主体の使い方をしてみることで(例えば plotSpector .5 D65# + .5 D50# & という風に)、「純関数(無名関数)」を使うことにも慣れてくるといった副次的な効果もあるかもしれません。

■「無名関数」と「吾輩は猫である」　

　夏目漱石の「吾輩は猫である」は、雑誌「ホトトギス」に1905年1月に発表された。最初は、冒頭の章だけで完結する短い読み切り小説だった。

　吾輩は猫である。名前はまだ無い。　…吾輩がこの家へ住み込んだ当時は、主人以外のものにははなはだ不人望であった。どこへ行っても跳ね付けられて相手にしてくれ手がなかった。いかに珍重されなかったかは、今日に至るまで名前さえつけてくれないのでもわかる。

　「吾輩は猫である」を連想したのは、Mathematicaの「純関数」の勉強のための練習題材を書いていたときだ。Mathematica の入門・中級の講習会に参加すると、この純関数とやらが登場した途端に、講師が話す内容を見失ってしまうことが多い。講師の筋道が見えなくなってしまう理由は、純関数の必要性・存在価値といったものが今ひとつわからないままに、純関数がいきなり登場してくるからである。もちろん、「（数値でなく）関数を引数として与える」ということに慣れていない生徒が多いこともあって、いつも、純関数が登場した瞬間に、何かその場が失速したような感覚を受ける。

　話の流れ・必然性がなくても、文法をただ暗記することができる人であれば、おそらく何の問題もないのだと思う。あるいは、他のプログラミング言語をよく知っていて、文法の必然性が自然と理解できる人たちであったなら、これもまた問題は起きないのだろうと思う。しかし、私も含めて、入門・中級の講習会に来ているような、そうでない多くの人たちの場合は、純関数が登場した途端に、話についていけなくなることが多いように感じるのである。

　Mathematica における純関数 "Pure Function" というのは名前(シンボル)を持たない関数で、ほかの関数への引数などとして、関数の内容を書いた一瞬だけ使われるものだ。もう少し違う呼び方をしてしまえば、つまりそれは「無名関数」だ。「無名」というところが重要で、名前がないから、使ったら最後もう二度と呼ぶ・使うことはできない、ということである。つまりは、「使い捨ての関数」だ。この「関数を使い捨てる」というところで、どうしても引っかかってしまう。値を入力するのであれば、あまり考えることなどせずに、数字キーを2・3回押せばすむ。だから、値に名前（シンボル）と付けずに、使い捨てにすることには慣れている。けれど、関数を書く場合には、（ハッカーでない私たちは）頭も多少使わざるをえない。すると、せっかく考えて・苦労して書いたのだから、名前をつけて、あとで呼んでまた使うことができるようにしたい、などと思ってしまうのである。使い捨ての「無名」ということと、苦労をともなう「関数」ということを、なかなか重ね合わせることができないのである。

　そこで、自分なりの「純関数の存在価値・意義」を作ることで、その存在意義を納得したくて、純関数を使った例題を作ってみた。実は、それが前回の Spectrum Color Conversion を動かしているベース部分、「離散化を必要としない連続的なスペクトル演算・表示を扱うためのパッケージ」である。これは、無名関数（純関数）を使うための例題である。このパッケージを使うと、スペクトルを描くのに、

plotSpector[ (128 red[#] + 255 blue[#])& ];

(128 red[#] + 255 blue[#])&

rgb=fitSpector[(D65[#]-128 cyan[#])&,red,green,blue]

　こんな例題を作ることで、無名関数アレルギーが低減した、と言いたいところなのだけれど、関数を使い捨てることには、やはりまだ慣れることができそうにない。関数を引数として渡すことは自然に感じられるようになっても、無名関数に名前をつけて、再度その関数を呼んでみたい気持ちはなかなか止められそうにない。名前をつけるより、その関数の中身をそのまま書いた方がわかりやすいとわかっていても、単純な名前をつけてしまいたくなる欲望はなかなか止められそうにない。

　その理由を考えてみると、やはり、苦労をともなう「関数」を使い捨ての「無名」にしてしまう、ということに一因がある。そして、もう一つ、名前をつけることで、単純化して安心してしまいたくなる、ということがあるように思う。ほんの何文字かの関数であっても、その内容を自分の頭で考えるよりは、なにがしかの単純な言葉で表現された関数名を聞いて納得したくなることがあるように思う。

　「吾輩は猫である」の第一章の最後、つまり、当初の読み切り短編小説「吾輩は猫である」はこのように結ばれる。

　吾輩は御馳走も食わないから別段 肥りもしないが、まずまず健康でびっこにもならずにその日その日を暮している。鼠は決して取らない。おさんは未だに嫌いである。名前はまだつけてくれないが、欲をいっても際限がないから生涯この教師の家で無名の猫で終るつもりだ。

■「送籍」と「名前」　

　図書館は5階建てだが、人でにぎわっているのは1階だけだ。少し前に出版された本が置いてある２階より上には、ほとんど人がいない。人がいない２階で、無意識のうちに1冊の文庫本を手に取っていた。本を手に取ったのは、本当に無意識の一瞬のことで、気づいたら書庫から本を抜き出していたというのが的確なところである。その本を手に取った理由をあえてつけるなら、その本が「コロンブスの卵」という名前で、ちくま文庫だったからだと思う。「コロンブスの卵」という題名は科学的・工学的なものを感じさせるし、ちくま文庫はとても読みやすい文字レイアウトだという感覚が意識の底に染みついていたからに違いない。

　その本を抜き出すと同時に本の頁を開いた途端、少し驚いた。開いた頁に、「徴兵忌避者としての夏目漱石」という考察が綴られていたからだ。「展望」の昭和44年6月号に掲載されたという、丸谷才一の「徴兵忌避者としての夏目漱石」がそこに載っていたのである。前から読みたいとは思っていても読むには至らず、しかし内容が気になり数日前にも関連記事をブックマークしたりした、それらの記事の源流がそこにいきなり出現したので、驚いたのである。

　私の友人で送籍という男が「一夜」という短編を書きましたが…
1905年　「吾輩は猫である」

　これまで、半藤一利や北村薫の著作など、漱石の名前の由来を巡る話として「徴兵忌避者としての夏目漱石」の名前を出したものを読んでいた。しかし、「徴兵忌避者としての夏目漱石」は、徴兵忌避のために漱石が北海道へ籍を移した（送籍）ことが、漱石の神経衰弱の大きな理由になっていて、徴兵忌避の自責という視点から眺めてみれば、「こころ」の不可解な結末（乃木大将が出てくる必然性）も納得できる、という内容だった。漱石という名前が、「負け惜しみが強い」という意味の「石に漱ぎ流れに枕す」だけでなく、「送籍」をも意味するのではないかというような内容は、「徴兵忌避者としての夏目漱石」では書かれておらず、あくまで「こころ」に至るまでの背景・構造解説に集約された内容だった。

　「徴兵忌避者としての夏目漱石」の内容はとても自然なものだっただけれど、それとは別の、自然ではない「漱石の名前の由来を巡る話」にも、やはり興味を惹かれる。夏目漱石が最初に漱石という名前を使ったのは、1889年5月の「七艸集」上であって、漱石が（徴兵忌避が可能な）北海道へと本籍を送籍したのは、その3年後の1892年4月であるから、夏目「漱石」という名前の第一の由来は「送籍」ではないのだろう。しかし、漱石の最初の小説「我輩は猫である」で、自分自身を「送籍」という名前で語っているのだから、やはり自身の送籍を意識していたに違いない。

　「詩人かも知れないが随分妙な男ですね」と主人が云うと、迷亭が「馬鹿だよ」と単簡に送籍君を打ち留めた。
1905年 「吾輩は猫である」

　「籍」は名前と住所のデータベースだ。英語で言い換えれば、レジストリである。Windows ユーザが日々悩まされているWindowsレジストリなら、名前と値が階層構造で格納されたものだ。名前などを鍵（キー）にしてそのデータベースを呼べば、値など必要な全ての情報が得られるわけである。籍を移動することで固定されない浮いた状態にしてしまう「送籍」ということからは、「名前が無い・固定できない動的なもの」を連想してしまう。

　小生は今日までただの夏目なにがしとして世を渡って参りましたし、これから先もやはりただの夏目なにがしとして暮したい希望を持つております
1911年

　博士号拒否の際に自身を「ただの夏目なにがしでいたい」と書いた夏目漱石は、その「なにがし」の部分を一つの明らかな言葉で置き換えること、すなわち自身を名付けることはできなかったのではないか、と想像する。この「なにがし」は、博士号という冠・名前を軽く扱う表現上のトリックであると同時に、実は「なにがし」の部分は、漱石にはこのように表現することしかできなかったのではないだろうか。本名の金之助をここに入れることは、もとより忌み嫌っただろうし、それが「漱石」という号であっても、一つの固定した意味しか持たない限りは、ここで使うには至らなかったかもしれない。何かを書くことで自身を作っていくことはできても、その自身にふさわしい名前を付けることは非常に困難なことだったのではないだろうか。関数の中身を長く書き続けることはできても、その関数を「短い言葉」で表現することは不可能だったのかもしれない、とふと思う。

　私はその人をつねに先生と呼んでいた。だからここでもただ先生と書くだけで本名は打ち明けない。これは世間をはばかる遠慮というよりも、その方が私にとって自然だからである。
1914年　「こヽろ」

■光スペクトル操作用のMathematicaライブラリ　

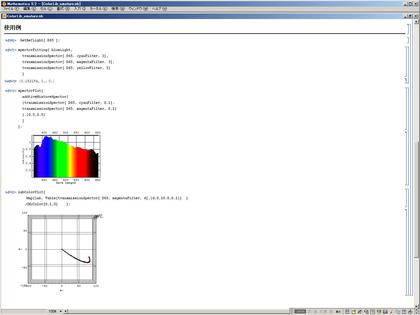以前、Mathematicaの演習用に作った「スペクトル操作用Mathematicaライブラリ」を少し直したので、ここ（”ColorLib_amature.nb”に置いておきます。以前作ったものと同じく、スペクトル・データをリストのような離散データではなくて、関数として（純関数＝無名関数として、あるいは、明示的な関数として）取り扱うという点が特徴だと思います。「（せっかくMathematicaで解くのですから）解析的に解く」「使用者には離散化・数値計算など、面倒くさい汚い部分は見せない・見たくない」という方針で作ったものです。

以前のものからの変更点としては、"spectorPlot"や"labPlot""labColorPlot"など、関数名のMathematicaの命名規則に合わせた変更、加法混色・減法混色用関数の追加・グラフ表示関数の追加・バグ修正といったところです。

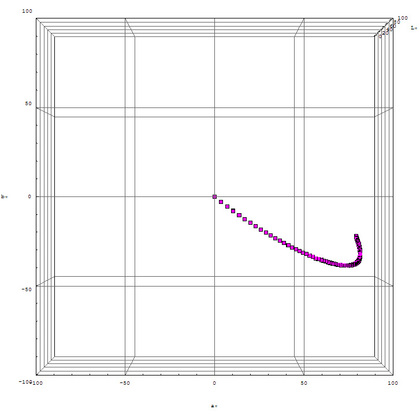　最初のラフスケッチが、絵画の原理を自分なりにおさらいするためのものだったので、濃度変調・面積変調などを扱おうとする場合には、比較的簡単に・気持ち良く作業ができると思います。たとえば、下記のようなコードを書けば、D65光源のもとで、赤紫色の絵具を重ね塗りしていったときの色の具合を CIE Lab 空間で眺めたりすることができます。

labPlot[
　Map[lab,
　　Table[transmissionSpector[D65,
magentaFilter, d],{d,0,10.0,0.1}]
]
];

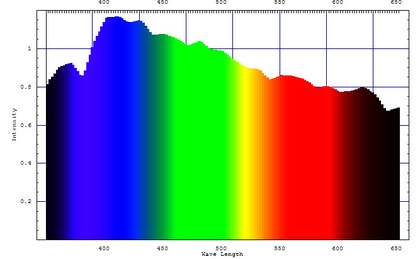　また、白色光照射時に黄色い絵具を塗り拡げる面積を増やしていった場合の反射光スペクトル変化をアニメーションとして作成・グラフ表示するコードはこんな感じです。"addtiveMixtureSpector"は加法混色用の関数で、"transmissionSpector"は減法混色用の関数です。お遊びソフトですが、色々遊ぶこともできるかもしれません。

Map[spectorPlot,
Table[
addtiveMixtureSpector[
{whiteLight,
transmissionSpector[whiteLight, yellowFilter, 1]},
{1-r, r} ],{r,0,1,0.1}]];

■分光スペクトル・色処理用のMathematica 7.0用ライブラリ　

　以前、「光スペクトル操作用のMathematicaライブラリ」というものを作りました。また、その習作として「スペクトル処理で遊ぶためのMathematicaノートブック」というノートブックを書いたことがあります。さまざまなスペクトル分布と持つ可視光を重ね合わせたり、塗り重ねたりしたとき、どんな色に見えるかを簡単に計算できる、しかもなるべく単純でいて応用しやすいようにしたい、と思いながら書いてみたライブラリです。

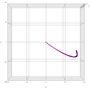
　たとえば、D65光源のもとで、赤紫色の絵具を重ね塗りしていったときの色の変化を CIE Lab 空間のグラフで眺めるには

labPlot[ 
  Map[lab,Table[
           transmissionSpector[D65,
                   magentaFilter, d],
                   {d,0,10.0,0.1}]
     ]
]; 

　ちなみに、このライブラリはMathematica 5.2で作ってみたものです。最近、Mathematica 7.0も使いだしました。すると、グラフィックス関連の関数の機能変更がたくさんあって、以前のライブラリでは表示関係のライブラリが動作しないことに気付きました。そこで、Mathematica 7.0用の「光スペクトル操作用のMathematicaライブラリ for Mathematica 7.0」を（まずは）適当に作ってみました。それが、ColorLib_amature on 7.0.nb (263kB)になります。

　ところで、Mathematica 7.0では、インタラクティブなアプリケーションも簡単に作成できるということなので、ColorLib_amature on 7.0.nbを使って、「D65光源の下で、白色紙の上にシアン色とマジェンタ色を塗り重ねていくとどんなスペクトルになるか」を表示するインタラクティブ・アプリケーションを作ってみました。その動作画面が、下の動画になります。上のスライダーがシアンを塗り重ねる量で、下のスライダーがマゼンタを塗り重ねる量を示しています。それぞれのスライダーを動かすと、「どんなスペクトルになるか」がグリグリと表示されます。

　さて、次回は、Mathematicaで作ったアプリケーションを誰でも使える形にして配布できるようにしてみたい、と思います。