1999-05-30[n年前へ]
■パーマンのパラドックス 
ボトルネックは何処だ?!
以前、
ハードディスクのエントロピーは増大するか?- デフラグと突然変異の共通点 - (1999.03.28)
の最後に「突然変異(あるいは、ハードディスクで言えばデフラグメント)のような現象が起きて、エントロピーが減少しない限り、熱的死(いや企業や会社であれば画一化、平凡化、そして、衰退だろうか)を迎えてしまうのだろう。」と書いた時に少し不思議な感じがした。それは、次のような矛盾を感じたのである。
まずは、
- 何事につけても、全体としての強さは一番弱いところで決まってしまう。
- 全体としての完成度を高くするためには、どこの強さも同じであるのが理想的である。
- 従って、全体を構成する部分というものは均質であるのが理想的である。
もし、ビルの鉄骨の一部に弱い所があれば、そこから崩壊が始まり、いずれビルが崩壊することは免れないだろう。
精度・力が高い所がいくらあろうと、「一番精度・力が低い所の=全体の精度・力」なのである。従って、一番精度・力が低い所を改良するのが全体としての完成度を高めるための唯一の方法である。
これは、モノであろうが、個人であろうが、グループであろうが同じである。例えば、写真を撮って出力することを考えよう。いくら写真の素材が良くてもカメラマンの腕が悪ければ駄目であるし、写真自体が良くても、写真の出力装置が悪ければ、それもやはり駄目である。そもそも、カメラマンが狙う被写体自体が悪ければ、答えはやはり同じである。
従って、精度・力を揃えた均質的な状態でなければ良いものは生まれないわけである。
これと、先の「画一化、平凡化、そして、衰退」すなわち、「画一化は良くない」ということの間に矛盾を感じたわけである。
しかし、少し考えてみると特に矛盾が無いことがわかる。ロボットを作る場合を考える。
- まずは一人で機械系も電気系もソフト部分も自分で作っていた。
- ソフト部分がどうも苦手なので、ソフトが得意な友達に手伝ってもらう。
- すると、電気系が比較的うまく行かないようだ。
- そこで、友達の友達に電気系を手伝ってもらう。
- それぞれ得意な部分で力を発揮し、特に弱いところもなくなった。
- ロボットの完成だ。
それでは、数学的にふざけたことを考えてみる。といっても、難しく考えるのではなく、中学生でも知っていそうなあの式を使うのである。
簡単の為にX,Y二つの部品からなるものを考える。それらの単独での精度(あるいは、出力)をx,yとすれば、全体としての精度(あるいは、出力)を考えると、それは(x* y)^(1/2)と置くのが自然だろう。それぞれ単独であれば、単なる和としては(x + y)/2であるわけである。ここで、2で割ったり1/2乗しているのは規格化しているようなものである(あとの落ちに繋げるためでもあるのだが...)。
今やりたいことは、(x * y)^(1/2)がなるべく大きくなるようにしたいのである。というわけで、相加相乗平均の関係式の登場である。
| x->(0,50),y->(0,50)の範囲で図示したもの | |
| (x+y)/2 ...相加 |  |
| (x * y)^(1/2) ...相乗 |  |
| (x * y)^(1/2)-(x + y)/2 ...相乗-相加 |  |

すなわち、x=yの時に(x * y)^(1/2)は最大になるわけである。良く知られている、相加相乗平均の関係式である。今回の話では、それぞれの精度・力が均質であれば理想的というのはこういったことである。異なる分野・方法で力を発揮しという方は簡単だ。異なる分野・方法で力を発揮するのでなければ、わざわざ乗算、すなわち、いっしょに組ませる必要がない。
さて、タイトルの「パーマンのパラドクス」であるが、少々疲れてきたので、本題は次回にしたい。今回はタイトルについての考察を上の話に絡めてしてみるに留める。
私は「パーマン」についてほとんど知識がない。TVアニメを観ていた記憶がある位である。だから、パーマンの名前の由来が何であるか知らない。スーパーマン+罰としての「パー」からきているのかもしれないが、ここで勝手な想像をしてみる。英語で考えてみると、par=同等、同水準、平均であるから、par-manは「平凡な主人公ががんばってスーパーマンになる」という気持ちが込められているのかもしれない。これはありそうな話である。
ここで、「平均」でなくて同等というような意味をそこに入れたらどうなるだろうか?パーマン1,2,3,4号に対して、par=同等、同水準、平均というような視点から考えてみるのである。あるいは、パーマンだけではなく、他で考えたらどうだろうか....
1999-12-16[n年前へ]
■スキー場の特殊相対性理論 
ジャンプの飛距離は何メートルだ?
突然ではあるが、HIRAX.NETのドメインレコードを調べてみると、
Record created on 16-Dec-1998.となっている。自分のドメインのレコードをわざわざ調べたのは、一体いつ取得したのか私自身が忘れてしまったからである。何しろ、「できるかな?」は当初異なる場所での二本立てで公開していたため、私の記憶がごっちゃになっているのである。あと各回の公開順序も実はかなりシャッフルされている。そのため、完全に忘れていたのである。
「できるかな?」はHIRAX.NETのコンテンツの一部である。しかし、HIRAX.NETの誕生日よりも、「できるかな?」の誕生日の方が実は早い。
で書いたように、「できるかな?」はすでに満一年を迎えていたわけである。そしてやっと、本日でHIRAX.NETも満一歳になったわけだ。何はともあれ、目出度いことである。子供の頃やらされた「ドリル」でも3日も続かなかったのに、1年続くとは、正に奇跡である。奇跡はそうそう続かないような気もするが... さて、関係ない話はここまでである。今回の舞台は万座温泉だ。なぜなら、先週末私は万座温泉でスキーをしていたからだ。何故だか理不尽な話しではあるが、私は万座温泉でローレンツ収縮を考える羽目になったのだ。もう少し正確に言えば、スキー場で特殊相対性理論を考える羽目になったのである。(先に断っておくが、私はトンデモ話をマジメな顔で言うことが多い。)
 |
話の発端はスキーに行く前に遡る。職場の今年の新入社員であるタカノリ君(仮名)とスキーの話をしていた。彼は秋田出身であり、子供の頃からスキー三昧の生活をしていた。大学に入り京都へ行ってからは、スキーをやる頻度は下がったが、チョコチョコ行ってはいたという。
そのタカノリ君(仮名)と話していると、彼はさりげなくこう言った。
「10m位のジャンプはよくするスよ。」10mである。2mの身長の人の5人分である。それは、スゴイ。
「えぇ、本当かぁ〜〜」
「いやぁ、そんなのよくやることじゃないスか?」
今回のスキー&温泉旅行は職場(と何故か競合他社)の人達30人程で行った。ほとんどの人は、割にスキーは好きな人が多い。従って、スキーも上手い人が多い。その人達に囲まれながら、タカノリ君(仮名)は断言した。
「6,7mは簡単だけど、10mってスゴイなぁ。」タカノリ君(仮名)、ただ者ではない。
「本当かぁ〜〜」
「えっ、だってただ飛ぶだけじゃないっスか。」
そこで、スキー場でその確認をしたわけである。場所は万座プリンスゲレンデの下部である。リフトとコースが交差する辺りに、ジャンプできる場所があったのだ。そこで、彼は軽く滑り出し、力一杯ジャンプした。
果たして、タカノリ君(仮名)は何メーター飛んだのであろうか? それとも、ただのホラ吹き男爵であったのだろうか?
ところが、その答えをすぐに書くわけにはいかないのである。なぜなら、タカノリ君(仮名)がジャンプをしてみせた時に事件は起こったのである。
「どうスか!10mはいったんじゃないスか!」
「3,4mしかいってねーぞ!おイ!」
これは、一体どうしたことだろうか? しかも、会話はまだ続くのである。
「何でっスか!軽く1秒は宙に浮いてたっスよ!」ますます不思議なことに、時間感覚すら違っているのである。一体何が起こっているのだろうか?
「そんなことはねぇぞ!コンマ数秒だろう!」
私はここで気づいたのである。観測者の間で時間と空間の不一致が生じているのであれば、ここはもちろんアレの登場である。アレと言えば言うまでもない、もちろん特殊相対性理論である。
そう、万座温泉スキー場ではローレンツ収縮を実感することができるのである。「スキー場でジャンプする」という現象を考える際には、「スキー場におけるhiraxの特殊相対性理論」を導入しなければならないのであった。
それでは、簡単に「スキー場におけるhiraxの特殊相対性理論」を説明しよう。今回、生じている不思議な現象は以下のようになる。
登場人物
- タカノリ君(仮名) 速度vでジャンプをしている。
- 観客 静止している。
| タカノリ君(仮名) | 観客 | |
| 飛んだ距離 | 10 | 3 |
| 飛んでた時間 | 1 | 0.3 |
つまり、速度vで飛んでいるタカノリ君(仮名)の感じる空間や時間といったものは、静止している観客に比べて、いずれも3倍程度に膨張しているのである。
通常の世界で生じるローレンツ収縮は、速度vで移動している観測者の空間軸も時間軸も
![]()
倍縮むのであるが(ここでは光速c=1の単位系を使用している)、
であるが、「スキー場におけるhiraxの特殊相対性理論」では、速度vで移動している観測者の空間軸も時間軸も静止している観測者に対して、逆に![]()
倍に延びてしまうのである。もし、ミンコフスキーの時空図を書いて確認しようとする人がいるならば、座標軸の傾きの変化も通常のローレンツ変換と逆に考えてみてもらいたい(その延長で考えていくと、矛盾があるというご指摘メールはノーサンキューである。)。
さて、そもそもローレンツ収縮は、マイケルソン - モーリーの実験結果(エーテルの影響が検出できない)を説明し、なおかつエーテルの存在を認めるために立てられた。それは、「運動体はすべてその運動方向に収縮する」という仮説である。その仮説を理論的に完成させたのが、アインシュタインの特殊相対性理論である(考え方としては根本的に異なるが)。
今回の話の中で「エーテル」に変わるのは、「空気」だろうか? いや、違う。私はむしろ、速度そのものであると、考える。つまり、特殊相対性理論と同じである。スピードを出して飛んでいるという感覚、速度が与える感覚の変化、すなわち速度そのものが、「スキー場におけるhiraxの特殊相対性理論」を要請するのである。
今シーズン、スキー場でせっせとジャンプをする人がいるならば、ぜひ「スキー場におけるhiraxの特殊相対性理論」について考えてみてもらいたい。
このWEBへ来る人の中で、同時期に万座温泉スキー場にいた人はいるだろうか?12/11.12に万座温泉スキー場のプリンスゲレンデの下部でジャンプにいそしんでいたのが、私達の一行である。そして、その中の一人(ショートスキーでせっせと飛び跳ねていたヤツ)はこんなことをずっと考えていたのである。
さて、実際のタカノリ君(仮名)の飛距離がどの程度であるか知りたいと思う人も多いだろう。オマエらの主観的な評価でなくて、実測定した距離を教えろと思う人も多いに違いない。
「絶対的な基準など存在しないから、そんなことは私はわからない。」と言い放ちたいところだが、タカノリ君(仮名)の名誉のために書いておく。彼が飛んだ距離は、2m弱のスキー板で4本分はあった。実は、タカノリ君(仮名)の基準が一番正しかったのである。彼は、「やるときはやる有言実行の人」なのであった。
2001-01-13[n年前へ]
■オッパイ星人の力学 第四回 
バスト曲線方程式 編
先日、父から封書が届いた。二十一世紀にもなったというのに、e-mailでもなくて封書が届いたのである。これは、やはりアレだろうか。いい年にもなってるのに、クダラナイWEBサイトを立てているデキの悪い息子を厳しく叱るためだろうか?しかも、そのクダラナイWEBサイト(しかも、有害公式認定サイト)の名前が自分の名前(hirax)だったりするからだろうか?それとも、「本が出たなら送れ」とは言われても実は送りたくなかった「あの本」を、少し前に父に送ってしまったからだろうか?いや、それとも…そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう?と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は?」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。
これは一体、どういうことなのだ?と頭の中がグルグル&複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の
ヒトは異性をどう選ぶのか?そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。という東大大学院の東海林さんの語りもとても面白いし、バストサイズを5段階に変えた女性の合成写真を使い、男子学生300人にアンケートしたという実験とか、巨乳好きの性格が父から受け継いだものであるかを調べるために、父子間で性的好みが伝達されるかを調べる、などの話もとても面白い。最高である。(中略)小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。(中略)「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。
そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。
うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え(てみたりもす)る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万!」位のことを言ったに違いないのである。
しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
さて、一体バストの形状というものはどうなっているのだろう?これまでの「オッパイ星人の力学」では
- 半球モデル
- 円錐モデル
そしてもちろん、このモデルに対して不満を持つのは私だけではなくて「これらのモデルには私は納得できません。」というメールがたくさん送られてきた。それどころか、「本当のオッパイをあなたは知らないのではないですか?」という実に失礼?なメールさえ送られて来ていたのである。「それでは、参考までに本当のオッパイの資料でも送って頂けないでしょうか?」とは私は大人なので返事をしなかったが、ちゃんとしたモデルを作らないことにはこれからもそんなメールがまだまだ来るに違いないのだ。
というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という
- 水風船バストモデル
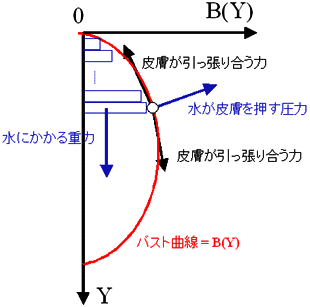
こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか?次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。(ちなみに、今回はバストを二次元の断面でのみ考えている。)
赤い線がバストの形状を示すバスト曲線
|
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか?
ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 |
まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか?とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
赤:すごくハリのあるヤングな皮膚の場合 |
この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前
の中でそう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだと書いたが、あれと同じである。今回は、年齢で変わっていくバストの皮膚のハリを「バストの皮膚のヤング率」とおいてみたのである。そういうわけで、皮膚のハリ= 皮膚のヤング率によってバストの形状は異なるわけだが、まずは眺めてみてもらいたい。以前のどうみても不自然な「半球バストモデル」等に較べて、ずっとましになっているとは思わないだろうか?特に、藍色・マゼンダのプロットなどかなり自然な形状になっていると思うのである。感受性の豊かなオッパイ星人であれば、必ずしやググッとくるハズである。
さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが(といっても、この図のアスペクト比に意味はないんだけど)、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
 |
個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。
また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ!だから、小さい方が良いのっ!」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。
ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。
今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。 H.Hirax, A.Kurotani
2001-07-27[n年前へ]
■SIRCAMと技術教育 
今回のSIRCAMはもう頻繁に色々なところから送られてくる。だが、だからといって「マイクロソフトのメールツールは使用しないことが、重要かと思います」という発言は思考停止だと私は思う。
少なくとも、今回はメーラーの種類は関係ないみたいだし、それに例えばそれは「刃物は危険だから使わないことが、重要かと思います」っていうのと近いものも感じるし。それでは技術教育とは矛盾するんじゃないのかなと思ったり、それはもしかしたら、生徒のほうが判っているんじゃないのかな、と思ったり。
2003-10-21[n年前へ]
■あなたは自分自身を記述できますか…? 
そして、もう一つ。「あなた自身がどんな人間か」なんてあなたは本当にわかりますか?人間がもっとも一番よく見えないのが自分自身ではないでしょうか。自分の眉毛が見えないのと同じく、自分自身がどんな人間かということは本人が一番判らないものです。
だから、自分自身を記述しようとすると、それはたいていの場合間違った記述になります。「『クレタ人はみな嘘つきだ』と言ったクレタ人」のパラドクスの例をひくまでもなく、自分自身を参照しようとする「自己参照」はえてして色んな矛盾を引き起こすだけのものだったりします。
だから、「あなた自身がどんな人間か」を自分で決めた後に、引き寄せられてくる「おとなり人間」には私はずいぶんと怖いものに感じてしまうのです。