1998-11-12[n年前へ]
■無限音階を作ろう 
上昇し続けるって何ですか?
無限音階を作りたい
無限音階というものがある。ド・レ・ミ・・・と音がどんどん高くなっていくように聞こえるのだが、いつまでたっても終わらず、ふと気づくとずっと前と同じような音の高さだというものである。Escherの無限階段の版画は有名だが、あれの音階版である。とにかく、無限音階を作ってみようというのが今回の目的である。参考までに、Eshcerのことに関しては藤原康司氏のWEBhttp://www.pluto.dti.ne.jp/~fwhd5468/に詳しい情報がある。 ちなみに、このような版画である。
 |  | 「上昇と下降」(左図、1960年作) 「滝」(右図、1961年作) |
無限音階の仕組み
人間の聴力にはもちろん周波数特性がある。ニコンの補聴器のWEBhttp://www.nikon.co.jp/main/jpn/society/hocyouki.htm
によれば20Hz-20kHzが通常聞こえる周波数の範囲であるという。例えば、CDのサンプリング周波数はが約40kHzであるのは、この20kHzの倍だからである。つまり、ナイキスト周波数による。
もし、ある高さの「ド」の1オクターブ下、そのまた下、...それだけでなく、1オクターブ上、そのまた上...が一度になったら、人間の耳にはどう聞こえるだろうか。それは、やはり「ド」である。その時のスペクトルはこんな感じである。なお、横軸は2をベースにした変形の対数軸である。また、実際には「ド」ではない。
 |
それでは、そのような「レ」が鳴ったとしたら?もちろん、それも「レ」である。そのようにして、「ドレミファソラシド」とやるとどうだろう?最初の「ド」と最後の「ド」は全く同じになっている。しかし、人間の感覚としてはどんどん音の高さが上昇していくように感じる。これが無限音階の仕組みである。
図で示すとこのようになる。なお、下の図中で水色は人間の耳に聞こえる周波数領域である。また、振幅はたんなる相対値である。
 |
 |
 |
 |
 |
作成した無限音階
今回は12音の平均率音階を用いている。音階そのものについては「音階について考える」という別の話である。また、基本波形としては正弦波を用いている。20Hz以下の正弦波を基本波形として、その倍音を20kHz超まで均等に足しあわせたものをただ作っただけである。正弦波を用いたのは話を単純化するためである。ここに今回作成したMathematicaのNoteBookを置いておく。また、下が作成する途中のデータである。どこか間違っているような気もする。少し不安だ。
 |  |
 |  |
さて、これが作成した無限音階である。それっぽく聞こえるだろうか。
1998-12-19[n年前へ]
■音階を勉強する 
単音シンセサイザーをつくる
今回は、音階そのものについて勉強をしてみる。世の中には色々な音階がある。いわゆる12音階の中でも、純正調、平均率などいろいろある。12音階でないものもある。どのような音階があって、それぞれどのような音程になっているのか調べてみたい。といっても、まずは7音音階、すなわち、ダイアトニックスケールだけを考える。
参考文献は手元にあった、「音楽の不思議」 別宮貞雄 著 音楽之友社である。なお、江尻氏の音律周波数表、音律について、音律実験(http://www.tg.rim.or.jp/~ejiri/)では色々な音階についての情報を知ることができる。5音階、すなわち、ペンタトニックスケールについての情報もある。同様なWEBサイトととしては「調律法ききくらべのページ」(http://www.top.or.jp/~murashin/index.htm)がある。ARATA氏の「MIDIで古典調律を」(http://www.nifty.ne.jp/forum/fmidicla/htmls/kotenj.html)にもかなりの情報がある。
ここでは、簡単にピタゴラス音階、ツァルリーノ音階(純正調音階)、12平均率だけを考える。
まずは、ピタゴラス音階を作る。Aという基準音を作る。その音に対して振動数が3/2倍の音をEとする。更に、Eに対して振動数が3/2倍の音をBとする。また、Aの振動数に対して、3/2倍の音をDとし、Dの4/3倍の音をGとする。そして、CGの3/2倍の音をCとする。最後に、Cの4/3倍の音をFとする。
各音の倍、あるいは1/2の音のオクターブ違いの音を考えると、結果としてC,D,E,F,G,A,Bのダイアトニックの7音音階ができあがる。このピタゴラス音階は旋律が良く響くという性質がある。よく響くという言い方は誤解を生じるかもしれない。「うまく旋律がおさまる」といった方がいいかもしれない。
| D/C | E/D | F/E | G/F | A/G | B/A | C/B | |
| ピタゴラス音階 | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 |
| ツァルリーノ音階(純正調音階) | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 |
| 12平均率 | 2^(2/12) | 2^(2/12) | 2^(1/12) | 2^(2/12) | 2^(2/12) | 2^(2/12) | 2^(1/12) |
次に、ツァルリーノ音階(純正調音階)は、各音の間の振動数の比を見てもわかるように、和音はよく響く。しかし、旋律として聞いた場合には、必ずしも良いわけではない。しかも、転調はできない。現在、一番使われている12平均率は振動数比をみてもわかるように必ずしも、和音の響きが良いわけではない。しかし、周波数を見てもわかるようにピタゴラス音階とツァルリーノ音階(純正調音階)の中ほどであり、和音の響き、旋律どちらも悪いわけではない。
ただし、1曲の中で厳密に音階が同じというわけでもないらしい。プロの弦楽四重奏などでの演奏では、必ずしも12平均率でなく、曲の中でも意識して音程を変えるという話だ。
また、ツァルリーノ音階(純正調音階)用に曲を作って聞いてみても、それほど良くなるとは思えない。確かにきれいに響くのだが、(私の感じでは)それだけなのである。
セントで表したものも示す。セントは基準音の振動数Nに対して、振動数Mである音を、1200x log_2(M/N) と表す単位である。 セントで表せば、12平均率は当然きりのいい数字になる。
| C | D | E | F | G | A | B | C | |
| ピタゴラス音階 | 0 | 204 | 408 | 498 | 702 | 906 | 1110 | 1200 |
| ツァルリーノ音階(純正調音階) | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 |
| 12平均率 | 0 | 200 | 400 | 500 | 700 | 900 | 1000 | 1200 |
音階についてあまり長々と考えてもきりがないので、ひとまずここまでにしておく。なにしろ、奥が深すぎる。最後に各音階の周波数表を示す。なお、Cの音はいずれも440Hzにしてある。ここでいうCは音名ではない、階名である。つまり、絶対的な音の高さを示すもの(音名)でなくて、相対的な音の高さを示すもの(階名)である。むしろ、よく使われるドと言ったほうが良いかもしれない。「Aをドにして歌ってみよう」という時の「ド」である。ところで、ドレミファソラシドの語源はどこにあるのだろう?SoundOfMusicがdoeの歌のイメージから"do a dear ..."と鼻歌を歌うことはあるが、語源は一体?次の宿題にしたいと思う。
さて、使用した周波数は全て江尻氏の音律周波数表、音律について、音律実験 (http://www.tg.rim.or.jp/~ejiri/)に記載されていたセントから最初の音を440Hzとし、周波数に変換してある。
| Hz | C | D | E | F | G | A | H | C | |||||||||
| 平均率 12Equal | 440 | 494 | 554 | 587 | 659 | 740 | 831 | 880 | |||||||||
| 純正律 Pure(5-3) | 440 | 495 | 550 | 587 | 660 | 733 | 825 | 880 | |||||||||
| 純正律 Pure(5-3)' | 440 | 495 | 550 | 594 | 660 | 743 | 825 | 880 | |||||||||
| 純正律 PureQ-39(3-5) | 440 | 489 | 550 | 587 | 652 | 733 | 815 | 880 | |||||||||
| 純正律 PureT-71(5-3b) | 440 | 495 | 570 | 594 | 660 | 760 | 855 | 880 | |||||||||
| メルセンヌ純正律 | 440 | 495 | 550 | 587 | 660 | 733 | 825 | 880 | |||||||||
| ピタゴラス律 | 440 | 495 | 557 | 587 | 660 | 743 | 835 | 880 | |||||||||
| 中全音律 | 440 | 492 | 550 | 588 | 658 | 736 | 822 | 880 | |||||||||
| キルンベルガー 第2 | 440 | 495 | 550 | 587 | 660 | 738 | 825 | 880 | |||||||||
| キルンベルガー 第3 | 440 | 492 | 550 | 587 | 658 | 736 | 825 | 880 | |||||||||
| キルン-ヴェルク | 440 | 492 | 552 | 587 | 658 | 736 | 828 | 880 | |||||||||
| ヴェルク 第1技法第3番 | 440 | 492 | 551 | 587 | 658 | 735 | 827 | 880 | |||||||||
| ヴェルクマイスター 第3' | 440 | 495 | 553 | 589 | 660 | 740 | 830 | 880 | |||||||||
| ラモー | 440 | 492 | 550 | 588 | 658 | 736 | 822 | 880 | |||||||||
| ヴァロッティ-ヤング | 440 | 493 | 552 | 588 | 659 | 737 | 826 | 880 | |||||||||
| ヤング 第2 | 440 | 493 | 552 | 587 | 659 | 737 | 826 | 880 | |||||||||
| 43平均律 | 440 | 493 | 551 | 588 | 658 | 737 | 825 | 880 | |||||||||
| 53平均律 | 440 | 495 | 550 | 587 | 660 | 733 | 824 | 880 |
National InstrumentsのLabViewのExample例の中でWindows環境でSoundを入出力するViがあったのでこれを利用する。また、その使用例としてプッシュホンの発信音を出力するものがあった。これを適当にいじって作ってみる。今回は簡単のために単音のみの出力である。いずれ、もうすこしちゃんとしたものを作ってみたい。
作成したアプリケーションをここにおいておく。
Onkai.lzh 1,176kB(配布終了です。)
LabViewのライセンス上、ダウンロード数が50近くになったら削除する。(配布終了です。)
 | まずは、赤丸部分のボタンを押して実行モードにする。 |
 | このように色々な音階を 選ぶことが出来る。 |
1999-01-03[n年前へ]
■オシロスコープソフトを作る 
PCを2Ch高性能オシロスコープにしたい
オシロスコープがあると便利だが、家で使うには敷居が高いし、値段も高い。まして、FFTアナライザーがついて周波数解析も行うことができるような機械になると、遊びで買うという値段ではなくなってしまう。そこで、PCを2Ch高性能オシロスコープにするソフトを作ってみたい。
以前、音階を調べた時に、SoundBlaster互換I/Fを使ったLabViewのサウンド入出力のViを使用してみる。目標はとにかくオシロスコープと同じ使い勝手であること、使うのが簡単であること、そして、周波数解析などが簡単に行うことができること、である。入力として、音声入力を使用しているので、たいていのPCで使うことができるし、音声入力マイクが着いているPC(たいていのノートPCは着いているだろう)なら、マイク(あるいは入力端子)を用意する必要すらない。
というわけで、下がそのアプリケーションの画面。
 |
20KHz(ナイキスト周波数で言えば正確には10KHzか)までしか、使うことはできないが、ちょっと使いたい時には便利だ。特に、音声を解析したいならば、必要十分である。上の画面では口笛を吹いて、その音声波形を表示させ、周波数解析を同時に行っている。周波数ピークが表示され、1120Hzであるという表示がされる。
内蔵マイクを使用すると、ただアプリケーションを走らせれば、音声周波数解析が行える。もしも、比較的高性能なマイクがPCに着いているならば、リアルタイム振動解析すら行うことができる。もちろん、マイク入力端子に何らかの入力をすれば、どんな解析もできるわけだが、何の用意もせずにできるというのは便利である。例えば、うるさいデスクトップPCの近くへこのアプリケーションを走らせたノートPCを近づけると、デスクトップPCがなぜうるさいかを簡単に調べることができる。うるさいのは、ハードディスクの周波数なのか、ファンの周波数なのかすぐにわかる。
今回、作成したアプリケーションはここにおいておく。動作させたら、レンジを調整することを忘れずに。
Ocilo.lzh LZH形式 1,259kB (打ち止めです。あしからず。)
LabViewのアプリケーションライセンス上、ダウンロード数は50回までで、その数近くになったら削除することにする。
2000-02-13[n年前へ]
■競馬の写真判定とパノラマ写真 
パノラマ写真と画像処理 Part.2
前回 、
の時にi_matさんから頂いたメールを紹介した。i_matさんは- I*MAT The HomePage (http://www.nsknet.or.jp/~i_mat/ )
- atoz@gol.com (http://www2.gol.com/users/atoz/index.html )
さて、前回
これらのソフトのStack-Slice機能を用いれば「複数画像(動画)からの走査線抽出」ができる。その使用例と、その面白い座標軸変換について考えてみたい。と書いた。今回もまた「数日後には登場」と言った割には時間が経っているような気もする。しかし、ここのところ文字通り忙殺されていたのである。と、言い訳をしながら今回この作業をやってみることにした。しかし、このページは少々重くなってきた。まして、走査線の抽出の話は使用画像が多くならざるをえない。そこで、次回、詳しく使用例を紹介することにする。
よく、次回登場と言ったまま数ヶ月経つことがあるが、今回は大丈夫である。少なくとも数日後には登場することと思う(多分)。
まずは、
- 「複数画像(動画)からの走査線抽出」
- 「座標軸変換」
以下に示す連続の画像は競馬のゴール地点に競走馬が到着した瞬間である。「馬に見えない」という人がいたら、それは目がおかしい。誰がなんと言おうとこれは馬である。馬と鹿の区別がつかない人は馬鹿と呼ばれるが、これはとにかく馬なのである。
 視野の中に馬がもっと入ってくる。
視野の中に馬がものすごく入ってる。 |
さて、このビデオカメラで撮影された画像は例えば以下のようなものである。
 |
撮影された各時間の画像から、この画像の赤で囲んだところを抽出し、並べたらどのようになるだろうか?
それはこのようになるだろう。よくある競馬の着順判定写真である。
 |
一見、これまで眺めてきたビデオカメラで撮影された画像と同じように見えるが、全く違う。ビデオカメラの撮影画像の動画中における、複数画像間の「位置」は全く変化していない。変化しているのは「時間」だけである。
だから、このような赤い長方形の画像を並べた方向というものは「時間軸」を意味しているのである。それを、下の画像に示してみる。
 |
この画像は縦方向は「空間軸」であるが、横方向は「時間軸」なのである。ビデオカメラの画像が縦横共に「空間軸」を示しているのに対し、その一軸を「空間軸」から「時間軸」に変換したものなのである
この競馬の着順判定写真の場合、カメラは空間に固定され「時間軸に変化するもの」を撮影していた。だから、このように各画像から一部を抽出して並べると、それは「時間軸」に対する変化を示すものを得ることができる。
また、例えば実験条件を変えたときの計測画像に対して「各画像から一部を抽出して並べる」ということをするならば、それは「空間軸」x「実験条件」というものを表す画像を得ることができる。
それでは、時間的には変化しないものを、ビデオカメラで撮影する方向を変化させながら撮影したらどうなるだろうか?例えば、ビデオカメラを下のようにして360度回転させながら撮影をしてみるのである。
 |
この場合撮影画像の各画像は撮影方向角度が異なるわけである。従って、先ほどのように一部分を抽出して並べると、一方向は「空間軸」であり、もう片方の軸は「撮影方向角度」になる。結局当たり前ではあるが、ある位置から眺めた周りの景色が得られるわけだ。
これが、前回i_matさんの要望していた
- 8ミリビデオを横倒しにして、 モーター回転するヘッドでぐるりと360度撮影し、
- その撮影した動画ファイルの、各フレームから走査線にして数本分を抽出し(インターレースで256本のうちセンター128本目の前後数本の走査線分)、
- それを貯めて1枚のjpgファイルにする、
- そのJPEG画像をMakeQTVRPanoramaの入力にして、パノラマムービーを作る、
それでは、その作業を実際にしてみようと思う。i_matさんから送って頂いた動画ファイル
を使い- 動画から静止画に変換し(走査線の狭間-1/60秒の世界を目指せ- (1999.07.08) 参照)、
- Image PC(NIH-imageをWindowsに移植したもの)で、走査線の一部を抽出し並べた静止画を作成する
もういきなり結果を出してしまおう。これが、「動画ファイルから走査線を抽出し、パノラマ写真にしたもの」である。
 |
おや?何が何だかわからない画像になってしまっている。変なモザイクがかかったみたいな画像になっているし、グレイ画像である。参考までに、先ほどの動画から手作業でパノラマ画像を作成したものを以下に示す。上の画像と比較してみると画像の示すものの対応がわかるだろう。
 |
さて、今回の実験結果が
- 変なモザイクがかかったみたいな画像になっている
- グレイ画像である
まず、
- 「グレイ画像」になっている理由
そして、「変なモザイクがかかったみたいな画像になっている」のは(動画中の)各画像から走査線をそれぞれ一本しか抽出しなかったからである。だから、横方向(カメラの撮影方向角度)のデータが足りないのである。そのため、モザイク画像のようになってしまったのである。
本来、抽出する走査線の数は、カメラの回転速度に応じて増やしてやらなければならないわけであるが、それが上手く合っていなかったのである。また、今回の画像を見て頂くと判ると思うが、動画ファイル自体も、実は一秒辺りのフレーム数が間引かれたものとなっている。それにより、抽出する走査線の数が一本ではますます足りなくなってしまっていたのである。
というわけで、今回は「失敗した」と言わざるをえない。何か、前回は「簡単である」などと言い切ったような気もするが、それはきっと気のせいであろう。
やはり、これは適当にあるもので間に合わせ仕事をしようとしたせいかもしれない。いつの日か「mov2panorama.exe」を作成し、必ずや必ずや再挑戦をするつもりである(Macでやるのは少しあきらめモード)。
2000-05-27[n年前へ]
■ささやかだけれど、役にたつこと 
メール紹介の小ネタ集
「できるかな?」の話題に関して色々と面白いメールを頂くことがある。その中には、私の知らない色々な面白いことが書いてあるものも多い。今回はそういったものの一部から小ネタ集(探偵ナイトスクープの桂小枝風)をやってみたい。メールは多少こちらで書き換えている部分もあるが、基本的には頂いたそのままである。
まずは、
の時のように計算間違いをしたりすると、さまざまな正解がメールで送られてくる。非常にありがたいことである。簡潔に間違いの個所を指摘してあるメールもあれば、私と同じように迷路にはまり込んでしまった答えが書いてあるメールもある。どちらにしても、私にはとても面白く、ありがたいものである。 例えば、最近で言うとこんな面白い「間違い指摘メール」を頂いた。
早速ではありますがにてどんぐりころころ、どんぐりこと記述されておりますが「どんぐりこ」ではなくて「どんぶりこ」が正しい歌詞だと記憶しております。真偽を確認の後、然るべき行動を取られることを切に願います。 |
「えっ」、と一瞬思うが、口ずさんで、後の歌詞のつながりを考えてみると、確かにそうかもしれない。どんぐりがお池にはまるなら、確かに「どんぶりこ」の方が自然である。桃太郎の桃が「どんぶりこ」と川を流れてきたように、どんぐりも「どんぶりこ」となるのが自然である。
そこで、WEB上で情報を探してみると、
- どんぐりの歌( http://www.jstudy.ne.jp/~donnguri/html/dongurisong.htm )
そして、同じ「どんぐりころころ」ネタと言えば、こんなものもある。
| にて、 - 「どんぐりころころ」と水戸黄門の主題歌の輪唱 - というものを書かれておりましたが、「赤とんぼ」と水戸黄門の主題歌(あぁ、人生に涙あり)も輪唱可能 です。 他に思いついたのが、 おたまじゃくしは、カエルの子。ナマズの孫ではないわいなぁ。も、「あぁ人生に涙あり」の節でいけそうです。 どうも、山田耕作系の曲は合うようですね。以前、「山田耕作の曲は日本語の音韻律に合わせてある。」という話を聞きましたがこれが関係しているのでしょうか? 他に、昔TVで見たものですが、
|
私には水戸黄門の主題歌の題名が「あぁ人生に涙あり」であると知れただけでも、うれしくてたまらない。いいタイトルだ。日本人の心にグッとくるタイトルである。
そして、その後の
- 山田耕作系の曲と「あぁ人生に涙あり」のカノンについての関係性
と、思いつつなかなか手をつけられないでいるので、今回ここに紹介してみた。もちろん、いつか挑戦しようという気持ちは変わっていない。いつか、必ず登場させるだろう。
そして、同じ「モナ・リザ」つながりでは、こういう面白い話を教えてくれるメールもある。
| の福田繁雄氏とモナリザの微笑みで思い出したのですが、トーストの焦げ目で描いた作品を見た記憶があります(これが福田氏の作品だったかどうかあいまいなのですが)。この時の作品は、焼け具合の違うトーストを並べてありましたが、展示が終わった後はどうしてしまったのでしょうか。 インドあたりでやってる砂で描いたマンダラに通じるものがあると思いました。(その場限りのものという意味で…) |
このメールを読んでから、「モナリザ」の自己相似形ソフト 料理材料編 に必ず挑戦したいと考えているのである。そのために写真満載の料理ブックも購入してしまった程である。
他にも色々な知識と言えば、こんな情報もとても勉強になった。
で、ところで、ドレミファソラシドの語源はどこにあるのだろう?SoundOfMusicがdoeの歌のイメージから"doa dear ..."と鼻歌を歌うことはあるが、語源は一体?次の宿題にしたいと思う。とありますが、これはなんと、ドレミ....も歌からとられたもので、<聖ヨハネ賛歌>という歌の歌詞から引用したものだそうです。聖ヨハネ賛歌は当時使われていた、6音音階の各音を正しく理解、視唱させるために各行の開始音が6音音階の各音になっていた曲です。 つまり、聖ヨハネ賛歌の各行のはじめの歌詞が、Ut,Re,Mi,Fa,Sol,Laだったので す。 Do Re Mi、は、もとはフランス語のUt Re Mi Fa Sol La Si Utでしたが、16世紀になってイタリアで呼びにくいUtが現在のDoに変わったのでした。 |
こういう言葉が変化していく様子というのは私のとても興味のあるところである。そういう話、「蝸牛考」、あるいは探偵ナイトスクープの「アホとバカの境界線」のような面白い話があったら、ぜひ私まで教えてもらえるとうれしい限りである。
さて、最後にこんなメールをご紹介したい。これは、さまざまな色空間の多様性について書いたものについて頂いた意見の一部である。
| 複数種類の蛍光色素を用いて動物組織を染色し顕微鏡観察した画像をコンピュータで解析する技術が一般的になっています。ここで使われている疑似カラーが緑と赤ですが、私は緑と紫にしました。2色が重なるところは白くなります。通常使用される疑似カラーで赤を暗く感じることも問題ですが、もっと問題なのは、赤と緑の重なったところを黄色に表示した場合、緑と黄色が区別できないのです。 自分が赤の変わりに紫を使って、緑と紫、重なったことろが白としたのは、これであれば健常者の人でも赤緑色盲の人でも余容易に区別がつくと思ったからです。色盲の人は日本で5%ですがアメリカではその倍以上います。学会の会場や雑誌の読者の中にこのプレゼンテーションが理解できない人が10ー20%いたら、発表している人にも損が生じます。 |
この考えには私もずいぶんと影響を受けた。そのせいで
つくった自作ソフトの色はその方式に合わせたし、では他のソフトの画面をWEB上では色調変換して表示している。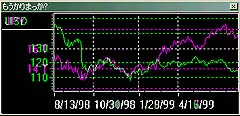 |  |
こういう「ささやか」なやり方ではあるが、私は緑-紫の疑似カラーの布教活動に勤めているのである。
今回は五通のメールを紹介してみた。その他にもたくさんの「面白いメール」を頂いている。別に技術的な話でもなんでもなくて、単に「こんな面白いことがあった」というメールを頂くこともあるが、それもまたとても私には役に立つのである。例え、現実的には「役立たなく」ても、それはとても「役に立つ」のである。
そんな「ささやかだけれど、役にたつこと」を今回はいくつか紹介してみた。そういうことは「どんなことでも」、こちら(jun@hirax.net )まで送ってもらえると、とてもうれしい。

