2000-07-29[n年前へ]
■The Spirit Level 
Fair is foul, foul is fair.
この写真は九州阿蘇山の麓にある京大火山研究所を撮影したものだ。草で覆われただけの小高い丘の頂上に、この火山研究所の建物はまるで灯台のように建っている。それはあまりに広大な景色だったので、手元にあった小さなカメラではそのままでは全景を撮影できなかった。しかし、「その広大で、それでいて箱庭のような景色の一部分だけを切り出す」ということはしたくなかった。そこで、近くにあったカーブ・ミラーを通してその広大な景色を撮影してみた。カーブ・ミラーの凸面鏡で反射させることで、広角の撮影をしようとしたのだ。だけど、それはとてもぼやけたミラーをだったので、ねじ曲がってただのよく判らない写真になってしまった。だけど、それでもその景色の一部分を切り出すよりは良かったはずだと思っている。
この写真を撮影したのは、もう10年程前のことになる。その夏、私は二週間ほど中国・九州を旅行していた。それは普通の旅行ではなくて、観測のための旅行だった。GPSによる標高測定と水準測量による標高測定を同時に行うことで、ジオイド(重力の等ポテンシャル面のうち平均海面と一致するもの)の形状を調べようとする研究のための観測だった。といっても、私は単なる下働きだったから、何にも考えずただ昼は力仕事をして汗をかいて、夜は温泉に入ってビールを飲む、という何だかとても幸せな二週間だった。
GPSによる幾何的な標高測定に対して、水準測量による標高測定は各地点における水平面を基準として標高を逐次的に測っていく。ところで、そもそも標高とは鉛直方向に対する位置である。それなら、一体鉛直方向とは何だろうか？それは、水平面に対して垂直な方向としか言いようがない。水平面が定まれば、一意に決まるわけだ。それなら、それは確かなものかと言うと、それは違う。
何故なら、水平面自体が場所によって違うからだ。水平面というものは単純なものでは決してない。その周囲(または遠方)の質量の分布によっていともたやすく変わってしまう。重力場が変化するのだから、当然の話だ。水が重力に引っぱられて、重力の等ポテンシャル面を形成するのだから、質量分布によって重力場が変動すればその等ポテンシャル面である水平面は当然のごとく変動してしまう。
水平面・水準といったとても基本的な基準でさえ、地球の内部や外部の状態でよくわからなくなってしまう。それは、ものを伝える言葉だって同じことだ。そもそもの原動力や背景があってこその基準や言葉なのだから、中にどんなものを秘めているかで物事の基準自体が変わってしまう。人が見ているものだって、その背景できっとみんな違っていると思う。それらは実のところ、とてもあやふやなものなのだ。
だから、Fairなんてとても大切な言葉だって、人によってその意味するものは違うのだろう。例えば、今ここで"Fair"を例に出したのも、"Fairis foul, foul is fair."というマクベスの冒頭のセリフを知っていれば、「あぁ、そういうことか」とその意味するところを判るだろうし、その背景を知らなければ「何でそんなことをいきなり？」と感じるだけだろう。それだけのことだ。
ところで、水準測定を行う時の必需品が"Spirit Level"である。この"SpiritLevel"という言葉は、直訳した 「心・生命の高さ・水平」なんて意味では全然なくて、単なる「水準器」という意味だ。簡単に言ってしまえば、単に"Level"だ。"Spirit Level"もグラスの中のアルコールを傾けてみれば、その語源は想像がつくだろう。
確固とした基準になりそうな水準器でさえ、実はそんなに確かなものではないのだから、何かの確かなものがあるという思い込みこそ、実はとてもあやふやなものだろうと思うのだ。
2001-07-25[n年前へ]
■遠い空のはて？
地平線の向こうに手を伸ばせ
先日、富士山の五合目へ行った。と一言で言っても、富士山の五合目にも色々ある。何しろ上り口が、第一人気の「吉田口・河口湖口」、下りの「砂走り」で有名な「御殿場口」「須走口」、そして測候所の白ドームを目指し最短距離一直線の「富士宮口」と四種類もあるのだ。その色々ある五合目の中で、先日私が行ったのは富士宮口の五合目というところだ。富士山の太平洋側から富士山頂に向かう登山口の標高2400m地点ということになる。もしかしたら、表富士五合目と言う言い方のほうが有名なのかもしれない。
その表富士五合目から下を眺めると、ずいぶんと遠くまで見えることに本当に心からビックリした。雲が下のほうに広がっていて、そしてその向こうに海や山や地平線が見える。そして、気のせいか地平線がとても丸いような気がする。その五合目までは車で簡単に来ることができたのだけれど、さすが標高2400mは伊達ではなかった…。やっぱり富士山は日本一の山かもしれない…。そして、そんな景色を眺めているうちに、私は色々考えてしまった。
あぁ、下を眺めると遠くまで景色が本当にきれいだ。そういえば、眺めると言えば…これまで、私は急な階段の下から上を眺めたらスカートの内側の下着なんかを覗けるかどうかをジックリ考えてみたりしてきたなぁ。それに、SONYの誇る可愛いらしいAIBOの気持ちになって、やっぱり同じく低いAIBOの視点から上を見上げたらやっぱりスカートの内側が覗けるかどうかを考えてみたりしたなぁ。見上げてばっかりだなぁ、しかも、どれもスカートの内側かぁ…。
そういえば、透け透け水着もマズかったなぁ…。あれ、本当に仕事の話から始まったんだけどなぁ…。誰も信じてくれないし…。あぁ、だけど、やはりそんなことを考えていてはいけなかったんだ…。そんなことをしてたから、画像処理追求サイトを目指したハズだったのに、何時の間にか有害サイト認定されてしまったりしたに違いないんだ…。ついには、「こどもに見せられないページ」保証までされたりするしなぁ…
私は一体何処で間違えてしまったのだろう…？ あぁ、それにしても地平線がきれいだ…。地平線が丸い…。 あぁ、地球はやっぱり丸いんだなぁ…。
と、まるで「生きる」で「ブランコに乗りながら人生を振り返る」志村喬のように、我が身を振り返っている内に、ふと「そういえば、地平線って一体どのくらい向こうにあるんだっけ？」と考えはじめてしまった。そもそも、地球が丸いからどうしてもある距離以上は見通すことができなくて、それが地平線なわけだけど、それは一体どのくらい先なのだったのだろうか？
おぼろげな記憶を辿ると、意外に地平線は自分の近くにあって、確かほんの数km先程度だった気がするのだけれど…。さて？あれ？ はて… 果て…？
というわけで、地平線までの距離を計算してみた。まずは、そのために下図のように視点の高さYと地球の半径Rをとってやる。
 |
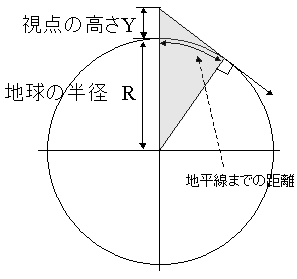「視点位置」と「地球中心」と「地平線」を結んだ三角形（グレーで塗りつぶした部分）がもう簡単なくらいに直角三角形なことに注目して解いてみると、「地平線までの距離」は「視点の高さY」の関数として
というような形になる（計算が合ってれば…）。これに、地球の半径R = 6400kmを代入してやれば、視点の高さYに応じた地平線までの距離が求められるわけだ。
そこで、まずは視点の高さが0〜3m位までの場合をグラフにしてみたのが次の図である。歩き始めて広い世界で暴れだすだろう頃の一才児の身長を緑○、そして、かつてはデカイの代名詞といえばコイツという存在だったアンドレ・ザ・ジャイアントの身長223cmを青○で記入してみた。
青：アンドレ・ザ・ジャイアントの身長 = 223cm  |
このグラフを見ると、一才児の地平線はおよそ3km先にあって、アンドレ・ザ・ジャイアントの地平線は5〜6km先にあることがわかる。もちろん、その間の身長の人達の地平線はその中間、そう4km先くらいにあるわけだ。私たちの地平線はほんの4km先、なんと走ればほんの20分位のところ、歩いても一時間かからない程度の近くに地平線はあるのだった。地平線なんていうと、遥か遠くにあるように思えるけれど、手の届くほんのすぐ先にいるのである。
そして、歩き始めた子供の地平線と巨人アンドレ・ザ・ジャイアントの地平線がたいして変わらない、というところも面白いものだ。あれだけ背が高ければ、さぞかし広い世界を眺めているのだろう、と思ったりするがそういうわけでもないのである。
じゃあ、もう少し高い場所に行くとどうか、ということで1000mまで視点の高さを上げてみたのが次のグラフである。東京タワーの特別展望台の250mを緑○で、あくまで計画中の秋葉原タワーの特別展望台の500mを青○で示してある。 ここまで上がると、250m地点で地平線は60km先になり、500m地点では80km程度先まで見通せることになる。東京駅の位置からの距離で言うと、60kmでは箱根くらい、80kmで三島くらいだろう。
青：計画中の秋葉原タワーの特別展望台  |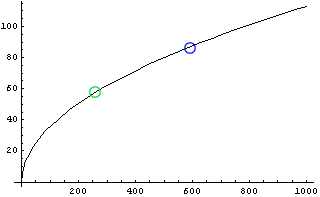
調子に乗って、さらに視点を高くしてみよう。先の表富士の五合目2400m地点では200km近く見渡せ、東京駅からの距離で言うと地平線は遠く浜名湖辺りまで離れていく。そして、さらにさらに視点を上昇させ、ジャンボジェット機の巡航高度地上10kmからであれば、なんと350kmほども見渡せるのである。350kmだと東京駅から京都くらいだろうか。東京-京都と言えば、そうちょうど東海道五十三次だ。江戸時代の人達が一月近くもかけて歩いたくらいの彼方まで地平線は後ろへ下がっていくわけだ。地平線は時が流れるにしたがって、遠くに広がっていくのだ。
青：ジャンボジェット機の巡航高度  |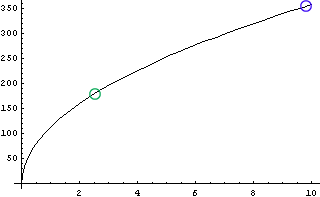
そのジャンボジェット機から見える地平線は、かつては一月近くもかけて歩いたくらいの遠く、400kmも遠くなのだから、そこまで行くと地平線が「遥か遠く」に思える。一瞬そう思える、のだけれど実はそんなことはない。ジャンボジェット機の速度からすれば、そんな遥か彼方の地平線だって、やっぱり30分ちょい位のすぐ近くだ。私たちが普通に立っているときの地平線が4〜5kmくらいのすぐ近くにあって、歩いてみればやっぱり30分ちょいで行ける、というのとほとんど同じなのだ。
ジャンボジェット機から眺めた地平線（水平線）
五歳くらいの子供の地平線と、空を飛び回るジャンボジェット機の地平線を時間を距離の単位として比較してみれば実はほとんど同じ遠さだ、というのは何だかとても面白い。大地の果てと天とが接っする地平線はとっても近くにあって、そこまで行くのにかかる時間は小さな子供でも巨大なジャンボジェット機でも同じなのである。
「地平線」なんて言うと、まるで「手が届かないもの」の代名詞みたいに使われたり、あるいは「その先には何があるのかわからないもの」の代名詞に使われたりするけれど、ちょっと行こうとして見れば、片道30分ちょっとでその「地平線」まで辿りつくことができるわけだ。案外、遠くにあると思い込んでいるものも、手を伸ばしてみれば、もしかしたら手が届くものなのかもしれない。しかも、それは地平線まで辿り着く時間が小さな子供でも巨大なジャンボジェット機でも同じだったように、誰でもできたりするものなのかもしれない。
もちろん、かつての「地平線」だった場所まで辿り着いたとしても、新しい「地平線」は視界の向こうに下がって行くわけなのだけれど、そこまでだってやっぱり歩けばほんの30分だ。遠い空の果て、地平線の向こうは、すぐそこだ。
2002-12-09[n年前へ]
■雪景色の箱根
会社の辺りは雪は積もっていませんでしたが、あともう少し`50mも標高が上がれば雪が積もっているような感じ。こんな景色も何処か遠くの景色に見える。遠くの雪景色の中を結ぶ送電線がとても不思議な感じに見える。
2003-02-08[n年前へ]
■日の出や湖面や槍ヶ岳
諏訪湖で日の出を眺めた。八ヶ岳の向こうから朝日がさしてくる。そんな朝日にデジカメを向けてシャッターを押してみる。少しきれい。そして、周りを眺めてみると、色んな山に朝日が差し始めてる。下を眺めてみると、諏訪湖では湖面をボートが滑つように動いてた。とても寒いけれど、きれいで静かな景色だ。
新穂高ロープウェイスキー場ではいつものようにゴンドラの中から槍ヶ岳を眺める。最上部が2200mで標高差日本一（知られていないけど）のスキー場だから、景色は本当に晴らしい。もちろん、狭くて急でコブで埋まるコースだって気持ちがいい。たまにコースを外れて小枝を避けながら、木々の中を滑ってみるのだって、とっても気持ちがいい。そんな感じで雪山の中を何にも考えずにただ滑る。陽はなかなか差してくれないけれど、ただひたすら滑ってみる。
2003-12-31[n年前へ]
■「一日」「新年」が始まる瞬間
「ヨチヨチ歩き」は1秒遅く、「つま先立ち」で0.05秒早く
最近、一日がとても短いような気がする。正確に言うと、一日が短いというよりは、夜の時間に比べて昼の時間が短いように感じる。ふと気づくと日が暮れていて、いつの間にか夜になっているような気がする。遙か昔の小学生の頃は昼の時間がとても長かったような気がするけれど、最近では昼の時間がとても短いように感じる。そして、昼の時間が短いだけではなくて、そもそも「時間」自体がとても短いような気がする。一年なんかあっという間に過ぎて、すぐに次の年がやってくるような気にさえなる。
江戸時代などであれば、普通の人々は日の出を「一日」の始まりとみなしていた。日の出とともに「一日」が始まり、そして「初日の出」とともに「新年」が始まると捉えられていた。だから、その感じ方に沿って言うならば、最近は刻々と日が昇るスピードが速くなっているような気がする。
そんな、日の出と共に始まる「一日」や「新年」であるけれど、「一日」や「新年」というものは誰にでも同じように始まるものだろうか？ …もちろん、そんなことはあるわけがない。東京にいる人とニューヨークにいる人では日の出の時間は大きく異なる。それでは言い方を変えて、例えばほとんど同じ場所にいる人、例えば同じ場所で並んで日の出を眺めるような場合であれば、「日の出」＝「一日の始まり」はほとんど同じように訪れるものだろうか？
もちろん、並んで日の出を眺めてみても、身長が違ったりすれば視点の高さが違うわけで、（単純な丸い地球を例に考えるだけでも）日の出の時間は当然その人の身長ごとに違うことになるに違いない。それでは、その「新しい一日が始まる時刻のズレ」「新しい一年は始まる時刻のズレ」というものは、一体どのくらい人それぞれ違っているものなのだろうか？
例えば、ヨチヨチ歩きをし始めるような一歳児であれば、平均的な身長は70cm程度だろう。そして、大人の女性であれば平均身長は160cm程度で、大人の男性であれば平均身長は170cm程度である。すると、それぞれの視点の高さは、60cm,150cm,160cm程になるだろうか。 こんな身長の人達が、元旦に東京（標高30m北緯35.41度）で初日の出を眺める時に、（もしも視界を遮る山が仮に無いとしたならば）それぞれの視点の高さからの日の出の時間のズレを算出してみると、次のようになる。
まず、身長170cmの(例えば)お父さんが160cmの高さの視点から日の出を眺める。その0.1秒後、日の出を眺めたお父さんが思わず感嘆の声をだし始める瞬間に、身長160cmの(例えば)お母さんの目からも昇ってきた朝日が見えるようになる。そして、お母さんが日の出を眺めてから少し時間が経って0.9秒ほど経った頃に、両親と手をつないで立っている一歳児の子供の顔にも太陽の光が差しこむようになる。0.1秒とか0.9秒という時間はとても短いほんの一瞬にも思えるし、意外に長い時間のズレにも思える。同じ場所にいる人には同じように差し始めるように思える日の出であっても人それぞれに結構違う時間であったりするのは面白いと思う。同じように（江戸時代のとらえ方で)始まるように思える一日や一年であっても、身長ごとに一秒近い時間のズレが存在するのである。ヨチヨチ歩きの子供は大人よりも約1秒遅く一日や一年が始まるし、身長170cmの人には身長160cmの人よりも0.1秒早く昼間がスタートするのである。
ところで、ヨチヨチ歩きの一歳児にとっては、元日の日の出は大人より1秒遅く差し込み、その一方で日の暮れは１秒早く訪れる。ということは、日の出から日暮れまでの時間＝日が差している時間を考えれば、大人よりも2秒短いということになる。小学生の頃の方が昼の時間は長かったような気がする- と思ったわけだけれども、子供から比べれば実は大人の方が２秒ほども昼の時間は長かったのである。
そしてまた、もしも身長160cmの人がつま先立ちをして精一杯の背伸びをすれば視点が5cmくらい上に上がって、その結果として日の出は0.05秒ほど早く訪れる。そうすれば、一日は0.05(秒)* 2≒0.1(秒)というわけで、日が差している昼の時間が0.1秒長くなることになる。逆に、日の出と日暮れ時にちょっと座って休んでみれば昼の時間が１秒ほども短くなる。こんな風に、私たちは秒単位で昼間の時間を長くしたり短くしたりすることができるのである。
だから、毎日が忙しくて時間が経つのがとても速く感じるときには、例えば高めのハイヒールを履いて、日暮れを0.1秒遅くしてみたり、…あるいは、なんだか疲れて一日がとても長く感じるときには、ベンチに腰掛けて日暮れを少しだけ早めてみるのも楽しいかもしれない。そんなテクニックを使わないにしても、こんな時間を操作するテクニックを知っていれば、日の出や日暮れが楽しく感じられるかもしれないし。
」など。