hirax.net::inside out::12月09日

■今日の万座　

　もう少し押さえ気味に滑れば良かった。滑ってるときは体調が良いように思えたのだが…（リンク）（リンク）

■スキーが上手くなる方法（素直でない人向き）　

　とりあえず、100cm位のスキーでツインチップじゃない板（後端が丸くなってないの）を借りて、それで滑ってみるのが良いのではないか、と。
　素直な人だったら、その人の滑り方をよく見て、その人に向く滑り方を教えてくれる良い先生かなぁ。そうすれば、新穂高ロープウェースキー場のパノラマコースを片足で滑り降りるくらいはできますよ、きっと。
（リンク）

■みんなで写真を貼り付ける地図サイト　

　前に見た記憶がありますが、何処だか思い出せません。その時は、写真はとても少なかったです。
　で、下のサイトなんか面白そうですね。とても私の好きな指向です。おや、もしかしたら多摩美大繋がりがあるかも…。（リンク）（リンク）

■今日見た景色 万座の雪景色　

　万座ハイウェイで。（リンク）

■今日見た景色 雲の切れ間の浅間山　

　浅間ハイウェイで。（リンク）

■師匠と弟子　

　万座でK郷さんとリフトに乗ってると、I東さんとI田くんがペアで滑ってたわけです。万座なら、あの二人が一緒に滑ってればなかなかに目立ちます。気持ち良さそうなその良いペアの滑りを見ながら、話題は何故かWきさんとロボS木さんのことになったのでした。
　そう、どれも師匠と弟子なんですね。

■CoolPix775壊れた？　

　金曜日に会社の駐車場とPAの駐車場で二度ほどCoolPix775を落とした。で、何ともないと思っていたのだけれど、シャッターを半押ししようとすると、いきなりシャッターがきれてしまう。
　「落としすぎだから、紐を付けて、首にぶら下げときなさい」と言われれば、その通りにしてきた私なのに、何としたことだ。このままでは、家には修理に出さないままのデジカメが３台になってしまう…。どうしよう？

■今日見た景色 南アルプス　

　今日の一時頃、眺めた景色。（リンク）

■今日見た景色 道は遥か向こうの南アルプスに一直線　

　国道141で清里を過ぎた辺りで。（リンク）

■数式処理プラグイン+ATOK15+Windows98　

　の環境下で「入力しているウィンドウのフォーカスをいったん他に移してから戻してやらないと表示されない」という症状が起こるとのメール。こちらでもその症状を確認しましたので、適当に直してみました。というわけで、アップデート版に差し替えました。
　具体的に直したところは、「AmetStartで他のWindowを作成してからすぐに消去していた」ところを「AmetResultでその処理を行う」ようにしました。
　また、Fさんのリクエストに応えて、"list"コマンドで自分で定義した変数定義一覧を出力するようにしてみました。
　Windows2000+ATOK13でのインストールが上手くいかない、というものについてはまた後ほど…（アドバイス募集中）。

■ただの「データベース＋パターンマッチング」　

　あとは方程式を解く機能でもあれば、どんなプログラムでもプチMathematicaみたいになるんだろうな、と思った。しかし、考えてみればMathematicaみたいな数式処理プログラムだってやっぱりただの「データベース＋パターンマッチング」なのだから、日本語変換のプログラムと同じに見えるのはそもそも当たり前なんだよな、と思ったのである。
　それにつけてもAMETプログラムもっとでてきても良いのになぁ…。なんでかなぁ。ATOKユーザーが少ないのかなぁ。やっぱり、MS-IMEのせいだろうなぁ、ことえりじゃないもんなぁ。それとも、voidさんのせいかなぁ。

■雪景色の箱根　

　会社の辺りは雪は積もっていませんでしたが、あともう少し`50mも標高が上がれば雪が積もっているような感じ。こんな景色も何処か遠くの景色に見える。遠くの雪景色の中を結ぶ送電線がとても不思議な感じに見える。

■ゴン太くんのひみつ　

　できるかな?といえばもちろんウラばなし できるかなに興味を惹かれるのである。

■クララのうそつき…　

　「ずっと憧れていたものに裏切られた経験ってありません？私と連れは世界名作劇場の「ハイジ」の世界にずっとあこがれていて、スイスにいきました。スイス自体は素敵な国でもう一度いきたいくらい気にいったんですが…。」に始まる「クララのうそつき…」

■愚者の楽園　

　「…すごいけれど、弱い私にはかなりキツイことです」と書く、あるプライベート日記。弱者はなかなか強者にはなれないし、強者は弱者をほとんど例外無しに理解し得ない。それは、弱者が正しいとか強者が間違っているなんていう話では決してなくて、単に「弱者はなかなか強者にはなれないし、強者は-弱者が弱者たる所以-をなかなか理解し得ない」というただそれだけの話だと思います。
　で、弱者は強者にはなかなかなれなくて、強者は弱者を理解し得ないのであるならば、「弱者と強者がタッグを組んだならば」それはさぞかし強いチームになれるのではないかな、と思ったりします。弱者の視点と強者の視線を兼ね備える「立体感」のある視線・力を持つチームになるのかも、と思ったりします。

　と、書く今回のタイトルはもちろん川原泉の「美貌の果実」に収録の「愚者の楽園」のパクリです。「人はいかにも愚かではありますが…」という「愚者の楽園」のパクリです。

■テキストと画像がズーミングするFlash(引数渡しバージョン)　

　jphoto3pなんていうのを昨日の夜に仕立てときました。　

■Flash for Linux　

　Flash for Linux。

■ノートブックPC色々　

　初めて買ったWindows PCが東芝のLibretto 20。すぐに、Libretto 50に買い換えて以降、色々なノートPCを使った。良かった辺りが、Toshiba Portege 320CT(修理を繰り返したが), Portege 3490CT(アキュポイントの作りを除けば最高に良かった), Thinkpad T42p。いずれも、小さく軽い割にパワフル＆大画面で、英語キーボードにトラックポイント（アキュポイント）ということ。 IBMがPC事業を売却したあおりで、Thinkpad が(デザインが最悪の)hpやDellやSonyのノートPCみたいになってしまったら、どうしようか。

■色んなiPod風　

　色んなiPod風とiPodペーパークラフト。

■頭と性格と体力　

　寺田寅彦の「科学者とあたま」を読むと、やはり藤原正彦を思い出す。危険な曲がり角や○×を志す人の性格条件/プログラミングと体力というような話だが、このエッセイを読んだことがない人は一読してみるのも面白いかも。知らない人は少ないと思うが念のために書くと、数学者である藤原正彦は父が「銀嶺の人」を書いた新田次郎であり(気象庁勤務時代に富士山レーダー建設に携わり、プロジェクトＸ 第一回の主人公にもなっている)、母が「流れる星は生きている」を書いた藤原ていである。

■ipod my photo　

　送付した写真をiPodのCM風な画像に変換するサービス。似たようなものを作ってみるのも面白いかも。 from 百式

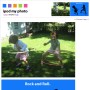
■地下鉄銀座線・旧新橋駅　

　地下鉄銀座線・旧新橋駅 from sawamurapid0309

■風船で空へ　

　たくさんの風船につかまり空に飛ぶ「ooning into the Sky」雲の上の空まで風船につかまって行ってみる。その様子(動画)を眺めると、(やる気になれば)なんでもできるような気にさせられるかも。 from BOX HEAD ROOM

■二日酔いしない飲酒量の計算式　

　「二日酔いしない飲酒量は計算式でわかる！」 from RandomNote

■裾野 / 桜木町 / 新橋　

　昼過ぎ、桜木町に行く。画像機器展の会場で、ふと気づくとわきさんがぬぼーっと立っている。そして、夜には、自分にはないものを持ってる色んな人たちを眺める。あぁ、みんながんばっているなぁ…。

■「女は生きにくい」　

女王様(私)はオヤジと呼ばれる抑圧的な男たちが大嫌いで、ずっと彼らを憎んでいたのだが、彼らを憎むと同時に己の女性性も憎んでおり、これでは敵であるオヤジどもと同類なのであった。女王様が和解すべきは、オヤジどもよりも先に…中村うさぎ　　「女は生きにくい」　週刊文春

■USBメモリで持ち歩く" Macintosh 128K and Plus" 　

　Creating a Mac-on-Stick using Mini vMac.

■自由に使うことができる写真集　

　「画像素材として自由自在に使って構いません」という「自由に使うことができる写真集」用の画像アップロードです。写真がまた貯まってきたので、近いうちに、「自由に使うことができる写真集２」用のスクリプトを走らせよう、と思っています。(2007.12.9)

■私たちの前にある「たくさんの古いこと」「数えられない新しいこと」　

　少し前、「栄光なき天才たち」の原作を書き、重力多体問題用スーパーコンピュータ"GRAPE"(分子動力学用途のものはWINEである)の実作業を主として担った伊藤智義氏が、高校の数年上の先輩にあたるということを知った。GRAPE関連の書籍などは色々読んでいたが、あのありふれた公立高校の校舎にいた人だとは、全然気づかなかった。この記事を読んで、なんだかとても嬉しい気持ちになったのだけれど、その嬉しい気持ちに忸怩たる違和感も、チリチリと感じた。

　その違和感の原因は、私自身が別に何をしているわけでないのに、嬉しく思う・感じるのはなぜなのだろう？と考えたからだ。もしかしたら、私の気持ちの底に「虎の威を借る狐」のような欲望があるのだろうか、と考えたからだ。

　「ふるさとは語ることなし」と、坂口安吾は死ぬ直前に書いた。ふるさとのように、ふるいこと、自分でない誰かがしたことは数え切れないくらいたくさんある。けれど、私たちができること・したいことも、まだまだたくさんあるはずだ。新しいこと・してみたいことは、私たちの前にたくさん積み上げられている。「ふるさとを語る」のは、まだ早い。

　坂口安吾のキーワードである「ふるさと」という言葉には、二重性というより、対極的で相反するものが、そのまま一つの言葉の中に込められているという気がする。
「桜の森の満開の下」解説　川村 湊

■「卓球ロボットvs.卓球人間」スゴイのはどっちだ!?　

　ロボットアームを作ろう!?と色々探しているうちに、こんな卓球ロボットを見つけた。アームの先に透明板とカメラを備えた"ROXY"は、人間相手に卓球をプレーすることができるロボットだ。

　「卓球ロボット vs. 人間」の実演動画(動画1,動画2)を見ているうちに、人間を相手にして卓球をプレーすることが可能な卓球ロボットもスゴイけれど、卓球ロボットとラリーを続けることができる卓球人間の方もスゴイ・・・と気づかされた。卓球ロボットの守備範囲に、実に見事にボールを上手に返し続けている。卓球ロボットが人間とラリーすることができるためには、卓球ロボットと同じように人間の方だって卓球テクニックがなければいけないわけである。

　もしも、この実演者がロボットアームの開発者でもあったりしたならば、もしそうだったりするならば、得意技術分野中には、ぜひとも「卓球」という項目を書き入れて欲しい。自分で作り上げたロボットを相手にラリーをし続けることができる「技術力」と「卓球力」・・・何だか面白い。

■エクセルの計算ワークシートをRubyでC言語に変換してみよう　

　この記事のスクリプトや、（下記のエクセルファイルとは違いますが、より有用そうな）エクセルファイル例、そして、そのエクセルファイルを変換したC言語ソースを保存し、また、つらつら考えことなどを「続　エクセルの計算ワークシートをRubyでC言語に変換してみよう」 に書きましたので、下記記事を読んだ後には、上記記事（さらにその後に続く記事など）を引き続きご覧ください。

　先日、「エクセルの計算ワークシートをRuby計算スクリプトに変換してみよう」でエクセルで作った離散化シミュレーション用.xlsシートをRuby Script（プログラム）に自動的に変換する、Rubyスクリプトを作ってみました。基本的には四則演算で（反復収束計算手法を用いることにより）「この世界を（エクセル上で）シミュレーションするスプレッドシート」を作ったなら、それを他のプログラミング言語に「変換する」アプリケーション例として、エクセルのシートをRuby言語に変換するソフトを作ってみたわけです。目標は「何だかすげー！、けど、役に立たねー！」です。

　というわけで、引き続き、今日はエクセルのシートをC言語に変換するRubyスクリプトを書いてみました。もちろん、今回も、基本的には四則演算と数値だけで作られ、反復収束計算手法を用いることで最終的な計算結果を得るような「シート」を前提にしています。

　というわけで、書いたコード"xls2c.rb"はこんな具合です。

require 'win32ole'

def getAbsolutePath(filename)
  fso=WIN32OLE.new('Scripting.FileSystemObject')
  fso.GetAbsolutePathName(filename)
end

def getAlphabet(n)
  val=n.to_f/25.0 
  mod=n%25
  result=''
  result+=('A'..'Z').to_a[(n-val)/25] if val>1
  result+=('A'..'Z').to_a[mod]
end

def defFunc(state,book)
  src=''
  book.Worksheets.each do |sheet|
    y=1
    sheet.UsedRange.Rows.each do |row|
      x=0
      record=[]
      row.Columns.each do |cell|
        if state==:def &&cell.Value.to_s!=''
          record＜＜'  float '+getAlphabet(x)+y.to_s+'=0.;'
        end
        if state==:init &&cell.Value!=''
record＜＜'  '+getAlphabet(x)+y.to_s+
            '='+cell.Value.to_s+';' if cell.Value.to_s!=''
        end
        if state==:calc &&cell.Formula!=''
t=cell.Formula.sub(/[=$]/,'')
record＜＜'  '+getAlphabet(x)+y.to_s+'='+t+';'
        end
        x+=1
      end
      if record.join('').gsub("\n",'')!=''
        src+=record.join("\n")+"\n" 
      end
      y+=1
    end
  end
  return src
end

filename=getAbsolutePath(ARGV[0])
excel=WIN32OLE.new('Excel.Application')
book=excel.Workbooks.Open(filename)
defsrc=defFunc(:def,book)
initsrc=defFunc(:init,book)
calcsrc=defFunc(:calc,book)
book.close
excel.quit
GC.start

puts ＜＜INIT
// autocreated C source from excel file
// jun hirabayashi jun@irax.net http://www.hirax.net

#include "stdio.h"

// gloval variables
#{defsrc}
void init(void){
#{initsrc}}

void calc(void){
#{calcsrc}}

int main(){
  int i;
  init();
  for(i=0;i＜10;i++){ calc(); }
  printf("C2=%f",C2);
  return 0;
}
INIT

ruby xls2c.rb ex.xls > sample.c

// autocreated C source from excel file
// jun hirabayashi jun@irax.net http://www.hirax.net

#include "stdio.h"

// gloval variables
  float A1=0.;
  float B1=0.;
  float C1=0.;
  float A2=0.;
  float B2=0.;
  float C2=0.;
  float A3=0.;
  float B3=0.;
  float C3=0.;

void init(void){
  A1=1.0;
  B1=2.0;
  C1=3.0;
  A2=1.0;
  B2=2.0;
  C2=5.0;
  A3=1.0;
  B3=2.0;
  C3=3.0;
}

void calc(void){
  A1=1;
  B1=2;
  C1=3;
  A2=1;
  B2=2;
  C2=B2+C1;
  A3=1;
  B3=2;
  C3=3;
}

int main(){
  int i;
  init();
  for(i=0;i＜10;i++){ calc(); }
  printf("C2=%f",C2);
  return 0;
}

　さて、このC言語ソースは、（たとえば、Borland C++ Compilerを使うなら）

bcc32 sample.c

　いつか、エクセルのシートを変換し・作成したC言語プログラムをコンパイルすると、どれだけ遅くなるのか・どれだけ早くなるのかを、色々な環境で確かめてみたい、と思っています。

■「汗のかきやすさは体重のルートに比例する」という「汗っかきの方程式」　

　太っている人は暑がりで、痩せている人は寒がりなのが普通です。単純に考えてみれば、人が発生する熱量は、おおよそ体重に比例するのに対し、体からの放熱は体表面積に比例するからです。太っている人、言い換えれば「体重（発熱量）の割に表面積（放熱量）が小さい、まるで球のような体型の人」はアッチッチになりやすいでしょうし、「体重（発熱量）の割に表面積（放熱量）が大きい、痩せぎす体型の人」ならあっという間に熱を奪われブルブル震えてしまうに違いない、というわけです。

　今日は「体重が増えると何倍暑がりになりやすいか」を考えてみようと思います。藤本らによる「実測値に基づいた日本人の体表面積の算出式」は次のようになります。

体表面積(cm^2) = 88.83 * 身長(cm)^0.663 * 体重(kg)^0.444

汗のかきやすさ= 0.0112575 体重(kg)^0.556 / 身長(cM)^0.663

　「体重が何倍になれば（横軸）何倍汗っかきになるか（縦軸）」を描いてみたのが右のグラフです。つまりは、「汗のかきやすさは体重のルートに比例する」という「汗っかきの方程式」を単純な場合で眺めた結果例になります。

　季節が変わり、冬の寒さを感じるようになりました。「寒さ」をふと感じたときには、「汗っかきの方程式」を頭に思い浮かべてみるのも面白いかもしれません。

■気象学的に探る「ゴッホの冒険」　

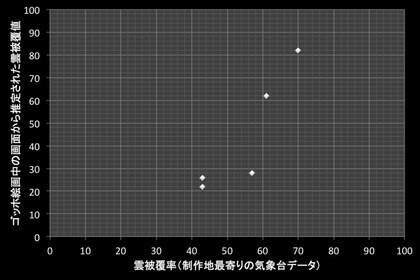
　"The Meteorological Odyssey of Vincent van Gogh ー気象学的に探る「ゴッホの冒険」(1990)"には、ゴッホの絵画に絵画に描かれた空が「どのくらい雲に覆われているか」を調べ・絵が描かれた地方の（実際の）気象データと比較した数値が示されています。

　その数値をエクセルでグラフにしてみたのが、下の図です。横軸は「雲被覆率（制作地最寄りの気象台データ）」で縦軸は「ゴッホ絵画中の画面から推定された雲被覆値」です。散布点（絵画が制作された場所）は、雲で覆われた比率が高い方から、オランダ、パリ、オーヴェル＝シェル＝オワーズ、サン＝レミ、アルルです。

　このグラフを眺めると、アルルやサン＝レミといった地中海沿いの街は、雲が多いオランダと違い、現実の世界もゴッホが描いた世界も、濃い空の色に覆われていたんだ…と感じます。そして、気象学データを使った絵画解説を読みながら「世界地図」を見ると、行ったことがない街へ足を伸ばしてみたくなったりします。

■Macbook用ACアダプタがバチン！と音立て壊れたので開腹してみる　

　朝、Apple Macbook Pro用で使っていたACアダプタが、バチン！と音を立て、電流を供給しなくなった。つまりは、壊れたのでケースを開けてみた。長ネジとナットを使いケースをこじ開け開腹してみると、ケース内側に２箇所焦げ付いた箇所がある。右の画像がACアダプタ内側で、右下の画像が、基板とケースを重ね合わせて示したものだ。

　焦げ付いた2箇所のうち一箇所はチップ抵抗。もう一箇所は、パッケージに穴が開いたチップがある場所。何だか面白くて、ルーペで眺めたり、顕微鏡で眺めたり、超拡大な3D撮影をしてみたりする。…関係無いけれど、一家に一台X線CT装置とか3D顕微鏡は欲しいと思う。