2000-06-08[n年前へ]
■うれしいひとこと 
10円でゴメンね。みんな愛のせいね。タイムドライバーは仮免。ベクトルの彼方で待ってて。Triangle On The Pavement。うれしいひとこと。あしたのあたし。恋は歌になれ。はい、チーズ! この言葉のセンスがうらやましい。
2000-10-06[n年前へ]
■恋の分水嶺 
ベクトルの彼方で待ってて
深夜に目が覚めてしまい、「探求心開発のすすめ - 「おかしい」と感じ、楽しく追求する事例集- 」北大路 剛 著 燃焼社セレクト教養双書ISBN4-88978-054-8を読んでいた。すると、「はじめに」面白い一節があった。
山の頂上が見えている間は、まだ、その麓にも達していない。山に登りはじめたら、山頂など全く見えはしない。次に踏み出す足をどの岩角に置くだけを考えて、少しでも高いところへ歩を運べば、やがて最も高い山頂に到達するはずである。「なるほどなぁ。そういうものかもしれないなぁ。だけど、仕事じゃぁそうはいかないような気もするがなぁ。頂上を極めるに至らなくても…とはなかなか言えないからなぁ。あと、次に踏み出す足の位置だけを考えていて、別の峰に登っちゃったらどうするんだろうなぁ。」などと思いながら惚けていた。すると、変なことを考え始めたので、それをここに書いてみることにした。
たとえ、頂上を極めるに至らなくても、その苦労に報いるだけのものは必ず得られるのだから。
次の図は「とある山」を示したものである。ちょうど富士山のような、広い裾を持つ孤立峰状の山である。
 |
この「とある山」における「少しでも高い方向」を示してみたものが次の図である。
 |
図中の各場所における矢印が「少しでも高い方向」を示したものだから、「少しでも高いところへ歩を運べば、やがて最も高い山頂に到達する」ことがよく判る。
とはいえ、その「少しでも高いところへ歩を運べば、やがて最も高い山頂に到達する」のは孤立峰だからで、次の図に示すような山脈ではそうはいかない。
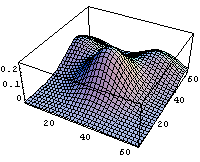 |
この図に示した山脈では、中央の山が他の山より高いのだが次の「少しでも高い方向」を示した図を見れば判るように、「少しでも高いところへ歩を運べば、やがて最も高い山頂に到達する」わけではない。下の図では青い線で示したような分水嶺が存在して、それぞれの領域の中で「少しでも高いところへ歩を運べば」、その近くの高い部分には到達するが、「やがて最も高い山頂に到達する」わけではない。当たり前である。
 青い線が分水嶺 人々はそれぞれ塗り分けた領域で一番高い山に到達することになる |
例えば、この図の向かって左上側から山に登り始めた人は、必ず青色の領域に入る。だから、青色の丸で示した頂上(実は一番高いわけではない)に登ってしまう。同じように、登り始めたのが右上なら、緑の頂上に登ってしまう。もし、赤色の丸で示した一番高い頂上に登ろうと思ったら、向かって下側から登らなくては頂上にはたどり着けない。
富士山のような形の山はそうそう見かけないのに対して、そうでない形の山はとても多く見かけるのだから、「少しでも高いところへ歩を運べば、やがて最も高い山頂に到達する」というのは実は一般的にはそうそうありえない話のように思われる。
さて、これはこれまでも考え続けてきた「恋」の問題についても同じだろう。次の図に示すように「マドンナ」が一人しかいない状態では、その「マドンナ」の周りの「恋ポテンシャル」だけが高くなっている。
 |
そのため、こんな「恋ポテンシャル」下での「恋のベクトル」を描いてみると、こんな感じになる。「男はみんな彼女の虜、彼女にみんな引き寄せられる」のである。「恋における孤立峰」での「恋のベクトル」の先には必ず「彼女(別につき合うという意味での彼女ではない)」がいるのである。
 |
それに対して、先程と同じようにこんな「恋の山脈」を考えたらどうなるだろうか?A子、B子、C子という三つの山からなる「恋の山脈」である。
 |
この場合の「恋の山脈」での「恋のベクトル」は先程と同じくこの図になる。つまり、あなたにとって客観的には一番魅力的なのはA子にも関わらず、恋の力に導かれるまま動いていったとしても、必ずしもA子に辿り着くわけではないのである。 さきほどの山と同じく、この場合にも「恋の分水嶺」があって、アプローチをし始める場所によって、B子の方に行ってしまったり、あるいは、C子の方に行ってしまったりするのである。ベクトルの彼方で誰が待っているかは、アプローチ次第だったりするのだ。
 |
というわけで、「実際の山脈」でも「恋の山脈」でも、「少しでも高いところへ歩を運べば、やがて最も高い山頂に到達する」わけではないのだ。
とはいえ、見晴らしのきく頂上に登ったりすると、今度は他の(もっと高そうな)頂上が見えてくるわけで、もう一度そっちへアプローチし始めるなんてこともあるだろうから、結局は「一番高いところ」へたどり着けることもあるのかもしれない。それに、「実際の山登り」でも「恋の山登り」でも道に迷ったりして、思いも寄らぬ方向へ行ってしまうことはよく?あるわけで、そんな時に「恋の分水嶺」を越えてしまうなんてこともよくありそうな事態ではある。
もっとも、「実際の山登り」ならともかく、「恋の山脈」の方では「結婚」なんて状態もあったりするわけで、実はそうそう他の場所へ動けない場合も多いだろう。そんなことを考えるだけでも、これまた大変そうな状況も想像されるのがオソロシイところだ。
そう言えば、この「探求心開発のすすめ」の「はじめに」の中には、私がもう一つとても面白いなぁと思ったフレーズがある。それは、
古くより、「必要は発明の母」と言われていますが、これにならえば「疑問は学問の父」であると言えるのではないでしょうか。という一節である。この一節からは何やら、
- 「必要」という足が地に着いている女、と
- 「疑問」という何か浮世離れした男
いや、何を書いているのだ。そんな話を書こうとしたのではなくて、つまり「色々な疑問」は「学問の父」ってことで、例えそれが結婚システムへの疑問だとしても、それは単に一例にすぎない、ってことで…
2001-03-22[n年前へ]
■種ともこ 
 「いっしょに、ね。」 「10円でゴメンね」のかっこよさといったら。
「いっしょに、ね。」 「10円でゴメンね」のかっこよさといったら。
「みんな愛のせいね」 一種独特の雰囲気を感じるのは私の気のせいではないはず。このアルバムは、CDになって入れられた「お茶の間で Dance」はひとまず除いておいて、全体での雰囲気を楽しむのが良いかも。
「CheChe-ByeBye」 まるでベストアルバムのような一枚。「タイムドライバーは仮免」はどっかのサブタイトルでも使ったような?
「ベクトルのかなたで待ってて」 これもサブタイトルに使ったような?
「O-HA-YO」 「Triangle On The Pavement」の時間の浮遊感覚はとても哀しいかなぁ。
「うれしいひとこと」 ラストの「うれしいひとこと」は、矢野顕子の「ひとつだけ」と同じくらい名曲だと思うんだけどなぁ。
「感傷」 ちょっと飛ばして、このアルバムのラストの「はい、チーズ!」の最後を聴いているといつも泣きそうな気持ちになるのは私だけじゃないはず。(リンク)
2002-02-20[n年前へ]
■「やおい」の評価演算子 
ベクトルの彼方で待ってて II
 東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
「福田X小泉っていうのは、結構上手くやっているのかな?」と私が言うと、おもむろに
「あれは、福田X小泉じゃなくて、絶対あれは小泉X福田なのー」とその記者が言ったのである。何を言っているのかその意味がよく判らないまま、「ん〜?」と私が首を傾げていると、繰り返し
「福田X小泉と小泉X福田は全然意味が違うのー」と言い始めるのである。何が何だか訳がわからない。じゃぁ、何か?小泉X福田だと小泉純一郎が総理大臣で福田康夫が官房長官だけど、福田X小泉だと福田康夫が総理大臣で小泉純一郎が官房長官になるとでも言うのか??政治の世界では、言う順番で総理大臣が決まるとでも言うのか?と私が口をはさむと、
「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」と言うのだ。なんだコイツ?政界は判るけど、やおい界って一体何処の世界の話だ??と、困惑する私も構わず、そこから延々と長い演説が始まった…。その大河ドラマのようにやたらと長い話を要約すると、
- やおい → 一部の女性が好む「男性同士の恋愛もののストーリー」のこと
- X → やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…
で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。 今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。
で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
まずは、色々な人物(実際の人物であったり、小説などの登場人物であったり)のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を
- 攻めベクトル
- 受けベクトル
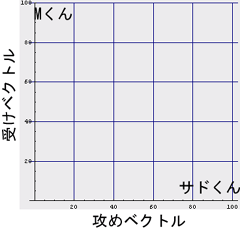 |
そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、
カップリング適性ベクトル = (攻め度(s)、受け度(m))と表記して、例えばAさんのカップリング適性ベクトルを(As, Am)と表すことにしてみよう。すると、Aさんが「攻め」でBさんが「受け」のカップリング適性は、この二人の適性ベクトルのベクトル積として表すことができる。つまり、
A×Bのカップリング適性 = ( As * Bm - Am * Bs )となるわけである。式を眺めれば判るように、Aさんの攻め度が高くて、Bさんの受け度が高ければ、この評価関数は高い値を返す。つまり、「A×Bの順序は正しいのだー」という評価を返す。つまり、「A×B」はなかなか良いカップルだー、と教えてくれる。また、もしAさんの受け度が高くて、Bさんの攻め度が高ければ、低い値を返す。つまり、「A×Bの順序は絶対間違ってるのだー」と評価してくれるのである。なんともありがたいことに(いや別にありがたくはないか…)、この「やおいのカップリング評価演算子」が「福田X小泉」と「小泉X福田」のどちらが自然なのかを教えてくれるのだ。試しに、上のサドくんとMくんであれば、「サドくん×Mくん」= (100,0)×(0,100) = 100*100 - 0*0 = 10000でとっても「良い感じ」でああるが、「Mくん×サドくん」= (0,100)×(100,0) = 0*0 - 100*100 = -10000で「このカップリングは絶対順序が違うー」と判るわけである。
= Aさんの攻め度 * Bさんの受け度
- Aさんの受け度 * Bさんの攻め度
とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか(?)「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。
ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。
これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。
一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。
「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
「愛はどんな形をしているか知っているか?」「見た事ないからわかりません。」「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう?... 異性愛か、同性愛か、そんなものじゃない …たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2002-04-24[n年前へ]
■視線のベクトルは未来に向くの? 
マンガのストーリーの方向を顔向きで探る 前編
一年くらい前から、コンビニで300円ほどの安いコミックをたまに買うようになった。休日の早朝、コンビニで発泡酒とおつまみを買って、ついでにそんな安いコミックを買って、そして、ビールを飲みながらそれを読むのがワタシの休日のささやかな(だけど至高の)幸せなのである。そんな至高の幸せをかみしめるとある休日、286円の西岸良平の「三丁目の夕日」を読みながら、ワタシはふと思ったのである。
これまで、「できるかな?」では、様々な小説、例えば「星の王子さま」「明暗」「こころ」「草枕」「失楽園殺人事件」といった小説を色々と解析してきた。そして、その中の主人公達がどんな風に動いていくのかとか、作者が何を考えているかとか、あるいは、犯人は誰かであるのか、などを調べてきた。何でそんなことを考えるの、と人には聞かれそうだけれども、とにもかくにもワタシはそんなことを考えてきたのである。そして、さらにふと考えてみれば、ワタシの至高の幸せを支える素晴らしき286円のマンガ本に関して、ワタシはストーリー構造などを真剣に考えてみたり、調べてみたりしたことはなかったのである。イケナイ、イケナイ、こんなことでは「恩知らず」野郎としてワタシにはバチが当たってしまうに違いないのである。
そこで、今回「コミックの中のストーリー構造」について調べてみたい、と思う。コミックの中で主人公達がどのような方向へ進もうとしているのか、あるいはその歩みの中で主人公達は一体何を考えているのか、などについて少し調べてみることにしたのである。
これまで、小説中のストーリー構造や主人公達の動く方向を調べるときには、「特定の言葉や主人公達」が登場する位置を調べたり、あるいは他の言葉や登場人物との相関を調べたりしてきた。それでは、一体マンガのストーリー構造や主人公達の動く方向を調べるにはどうしたら良いだろうか?そんなものどうやって調べるの?と一瞬悩んでしまいそうではあるが、ちょっと考えてみればそれはとても簡単なのである。小説と違って、マンガでは登場人物達がちゃんと見えるカタチで描かれているのである。主人公達がどの方向を向いているかがちゃんと描かれているのである。そしてまた、主人公やその周りの人々や、ありとあらゆる人々がどんな方向を向いているかがもうありのままにちゃんと描かれているのである。
だったら話は実に簡単、マンガの中の登場人物達の向きを刻々調べてみれば、そのマンガのストーリーの中で主人公達がどちらへ向かって何を見ながら動いているかが判る、というわけだ。実に即物的でシンプルなアプローチである。
善は急げ、というわけで、早速今さっきまで読んでいた手元に掴んだままの西岸良平の「三丁目の夕日 ジングルベル」の中から、「霜ばしら」という短編を題材にして、その中の主人公の顔の向きを調べてみることにした。ある恋人同士の、とても楽しくて、そしてとても悲しい物語である。
まずは、マンガのコマ中の登場人物達の向きと角度の対応表を下の表のように定めた。登場人物がコマ中で右方向を向いているときに0度とし、正面方向(すわなち読者方向)を向いている時が90度。コマの左方向を向いていれば180度である。そして、280度では真後ろを向いているという具合である。
270 | ||
180 | 0 | |
90 |
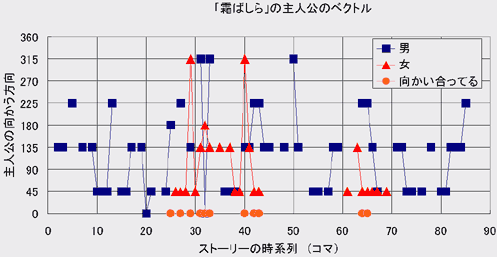
このようにコマの中に登場する主人公達の向きを数値化することにして、話の冒頭から結末までの各コマ中での主人公(周平)とその恋人(アキちゃん)の向きを調べてみたのが下のグラフである。青色の四角が主人公で、赤色の三角がヒロインである。また、その二人が向かい合ってる場合には朱色の丸を方向=0の位置に書き入れてみた。グラフ中では水平軸がストーリーの時系列で、左端が話の冒頭であり、右端が話の結末、そして縦軸が「主人公達の向かう方向」である。また、ヒロインのアキちゃんが途中の2カ所にしか現れないのは少しばかり悲しいストーリーのせいだ。この「霜ばしら」は主人公とアキちゃんの涙を誘う悲しい物語なのである。
左端 = 話の冒頭 右端 = 話の結末 縦軸 = 主人公達の向かう方向
|
このグラフを少し眺めていると大体の特徴が見えてくるだろう。すなわち、
- 主人公達はほとんど45、135、235度の3方向しか向いていない
- それ以外の向き(例えば315度)を向く場合などは、ほとんどが「向き合っている」場合である
- そして、135度の方向を向いていることが圧倒的に多い。
しかし考えてみれば、これらの特徴はごく当たり前なのである。まずは、舞台やテレビと同じく、登場人物達は読者にお尻を向けるわけにはそうそういかない。読者に顔を見せずにお尻を向けていたら、誰が誰だかよく判らなくなってしまうに違いない。だから、登場人物達はあまり後ろを向くわけにはいかない。どうしても、主人公達は文字通り「前向き」にならざるをえない。もし、後ろを向くとしたら、それは文字通り登場人物達に「後ろを向かせる」何らかの強い意図に基づく場合以外ありえないに違いない。それが、例えば他の誰かと「向き合って」いる場合であったり、あるいは他の表現意図に基づくものであろう。
また、日本におけるマンガが右から左に読まれていくのであるから、読者の視線の動きの中では「右のコマ= 過去」「左のコマ = 未来」と時間感覚が成立している。マンガを読む私たちの視線のベクトルは右から左、過去から未来へと進んでいるのである。すなわち、「マンガの中の話の流れ= マンガの中の時間・因果の流れ」をスムーズにするためには、主人公達が過去なり未来なりのコマの方向を向くことで、時間の流れ=因果の流れをスムーズに受け継ぐのが自然だと考えられる。過去に発生した「何か」に応えた反応をするならば、主人公達は当然右を向くし、そうでないならば通常は時間の流れる先の向き= 左側を向くことになるだろう。
すると、マンガの中の登場人物達は読者に対して「前向き」であって、なおかつ時間の流れる方向に前向きの「左側」を向くのがごく自然である、ということになって、「コマの中の主人公達は135度の方向を向くことが圧倒的に多い」ということになるのだろう。まぁ、当たり前の話である。
そしてさらには、こんな風にも考えられる。「右<->左」方向は時間の流れに対する主人公達の向きであって、「前向き<->後ろ向き」は登場人物達が文字通り「前向きであるか」あるいは、あるいは「後ろ向きであるか」という「主人公達の内たる気持ちの向き」ではないだろうか、とも考えられるのである。
だから、例えばこの「霜ばしら」の結末の部分80コマ以降を見ると、45->135->225度という主人公のベクトルの変化がある。これは主人公が「過去に向かう向き(死んでしまったヒロインへを見る向き)→未来に向かう方向へ進む→未来に向かう(だけど、やはり亡くなってしまったヒロインをたまに振り返りながら)」というまさに主人公のベクトルを描き出しているのではないだろうか、と思うのである。そんな風に眺めてみれば、最後のコマの主人公の向きが「何かを振り返りながら、だけど未来へと歩いていく様子」をまさに映し出しているようにも見えるのである。ストーリーはここに書くわけにはいかないけれど、こんな想像も割と良い線をいってるのかもしれない、と思ってみたりするのだ。
 |
こんな風に、単にマンガの登場人物の向きだけで主人公達の向かうベクトルを探る、なんていうことが乱暴なのはさらさら承知の上である。こんな人物の配置解析によるストーリー解析が的を射ているのか、あるいは的を外しまくっているのかは、ぜひこのマンガを読んで実際に判断してみてもらいたい、と思うのである。
さて、こんな風に舞台の右と左、上手と下手に対してどんな風に登場人物達が向かっていくのか、なんてことを考えるといろんな想像が広がってとても面白いのである。時間の進むベクトルであるLeftStage(舞台から見ると逆なんてことは言わずに)に消えていく登場人物達(例えば今回の話では恋人アキちゃんを亡くしてしまった主人公)は「残されたもの達」を連想させてみたり、あるいは、色んなものを眺める私たちの視線のベクトルは本当に未来に向いているのかな?などと色んな想像や空想を駆けめぐらせてみることも、それはそれでとても趣深いことだなぁと思うのである。