hirax.net::Keywords::「境界線」のブログ

■イベント・コンパニオンのヒミツ!?　

ミニか否かはハイヒール次第

　世の中には「知っている人は知っている。だけど、知らない人は全然といって良いほどに知らない」というコトが数限りなくある。例えば、「スクール水着のお腹部分には大きな穴が開いている」というスクール水着のヒミツもそんなコトの一つであるし、「ミニスカートの長さは32cmを境として見える見えないの境界線が決まっている」なんていうミニスカートのヒミツもその一つであった。
　知っている人には「何でいまさらそんなことを…？」と感じられるコトであっても、そのコトを知らない他の人にとってはそのコトは衝撃的以外の何ものでもなかったりするコトがある。「知っている人は知っている。だけど、知らない人は全然といって良いほどに知らない」なんていうコトほど、知っている人と知らない人の間の受け取り方のギャップが大きくなるものはないのである。

　そんな「知っている人は知っている」というコトの一つがsuchi today経由で知った右の写真から判る「イベント・コンパニオンの足下のヒミツ」に違いない。

画像はTECHSIDE　ビジネスシヨウ2003への直接リンク

　まずは、そのヒミツが隠されている右の写真をよく眺めてみよう。この写真を眺めてみてももしも何も感じなかったら、あるいはこんな写真や、こんな写真、あるいは、こんな写真を立て続けに見ると判りやすいだろうか。とにかく、どの写真を見ても「あぁこれは一点透視遠近法以外の何者でもないぞ」という感じを心の中で強く受けるハズなのである。見事なぐらいに画面の奥へ奥へと直線が伸びているようすを感じるハズなのだ。
　その理由はもちろん、コンパニオン達のつま先の位置も、スカートの端の位置も、視線の位置も全員が全員同じであるからだ。それはまるで、コピーして何人も複製して並べたかのように手前から奥まで全員が全員みんな同じなのである。そのせいで、コンパニオン達のつま先の位置も、スカートの端の位置も、視線の位置も、その全部が全部一直線となって画面の奥へ伸びているように見えるのである。

　もちろん、現実にこれらの写真の中のコンパニオン達がみんながみんなが身長であるわけも、足の長さも同じわけであるわけもなくて、そのコンパニオン達の足下をよくよく眺めてみれば、ハイヒールの高さを調節することで背の高さを調節していることが判るに違いない。もちろん、上に挙げた他のいくつかの写真をよく眺めてみても、やはり同じようにハイヒールの高さで調節していることが判るのである。それは知ってしまえば当たり前の話で、身長が低いからといって大きい服を着せてしまえばそれはとてもヘンであるし、身長が高いからといって短いスカートを履かせたりしたら、それはもっと大ヘンな事態に陥るに違いないのである。つまり、結局のところ

「各人それぞれの本当の身長」＋「各人それぞれの身長調整用ハイヒール」 = 「みんな同じ身長」

となっているわけで、つまりは「金正日(キムジョンイル) ナゾの9%」と同じ身長調整システムになっているのである。コンパニオン達の股下にあるけど足じゃない、コンパニオン達の膝下にあるけど何故か足じゃない、コンパニオン達には何かヘンな部分があるという「金正日と同じ身長調整システム」なのだ。

　しかし、「金正日と同じ身長調整システム」と同じということは、そのシステムを使った場合にはやたらめったら股下長さが長くなってしまうという弊害が現れるハズなのである。例えば「女性の身長v.s.股下比率」を見てみても、女性の足の長さは（身長が高い場合には比較的身長に占める股下長さが長いとはいえ）身長の 42～47%程度、つまりは身長の半分以下に過ぎない。しかし、このコンパニオン達のように身長を足下で調整してしまったりすると、その「各人それぞれの身長調整用ハイヒール」の高さが「各人の足の長さ」の中に繰り込まれてしまうのである。ということは、やたらめったら股下長さが（一見）長く見えてしまうのだ。それを言い換えるならば、そのコンパニオンの「足の長さだけがミョーに長く見えてしまう」のである。その人の体に比べてやたらに足が長く見え、そのスカートから伸びる足がやたらに長く見えてしまうのである。例えばそのコンパニオンが本当の身長にジャストフィットするようなスカートを履いていたりしたならば、その足を隠すスカートの丈が少しばかり（足に比べて）短く見えたりすることになるのである。つまり、そのコンパニオンがミニスカートを履いているように錯覚してしまったりするのである。

　とはいえ、コンパニオン達にとっては「足の長さが長くなってしまう」というのは別に弊害となるわけではない。足が長く見えるのは、それはとってもウレシイ話にしか思えないハズである。それを喜びこそすれ、悲しんだりするわけはないのだ。むしろ、その悲劇は一見無関係に思えるワタシ達傍観者の側に訪れるのだ。なぜなら、それらのコンパニオンに見とれるワタシ達は

1. スカートから伸びる足がやたらに長く見え、スカートの丈が足の長さに比べて短いぞ、と気づく
2. ということは、アレは結構なミニスカートだなと考えて（実は勘違い）、も・もしかして見えるかも… 、と期待をする
3. しかし、実際にはそのスカートが短いわけではないので（それにワタシ達は気づくこともなく）、無駄な時間を過ごしてしまう…

というような悲劇にワタシ達は陥ってしまったりするのだ。本来、コンパニオンそれぞれにジャストフィットしているハズのスカートを（ワタシ達善意の傍観者が）ミニスカートであると勘違いして見とれてしまったりするのである。特に短いワケでもないスカートに、特にナニが見える可能性があるわけでもないスカートにワタシ達は哀しくも一心不乱に見とれてしまったりするのである。

　しかし、「コンパニオン達が身長を足下で調整している」という簡単で「知っている人は知っている」事実を知っしまえば、実はコンパニオン達が「金正日と同じ身長調整システム」を採用しているという「イベント・コンパニオンの足下のヒミツ」を知りさえすれば、もう金輪際ワタシ達がこんな悲劇的なシチュエーションに陥ることはないのである。例えば、無垢なワタシ達がもしも何かのイベントに行ったとしても、まずは即座にコンパニオンの足下を確認し、「そのハイヒールがずいぶんと厚底である」と確認したならば、哀しげに首を振りながら「あのスカートは短く見えるけれどそれは目の錯覚で、本当は特に短くもないただのスカートなのだ」と自分を静かに納得させることができるようになるのである。そしてさらには、コンパニオン達の足下を見渡して、ハイヒールの「かさ上げ」がほとんどないコンパニオンを見つけたならば、「このコンパニオンのスカートは（短くは見えないけれど）本当は短いのだ」と心の中で喜びつつ、満足感と期待感とともにそのスカートに見とれることができるようになるのである。
　というわけで、イベントに行ったならばコンパニオンの足下をまずは確認すべし、そして低いハイヒール（という言い方もヘンだが）のコンパニオンを見つけてそのスカートに見とれるべし、というのが今回の「必ずトクする今日の一言」なのである。いや、ホントのところはどうだか知らないのだけれど…。

■アルキメデスのパンチラの式　

「スカート円錐」の明るさを探れ

「スカート円錐」の明るさを探れ

　以前、「ミニスカートの幾何学」として、女子高生の間などで流行っていたミニスカートの丈の短さの限界について考えてみたことがある。階段を上ろうとしているミニスカートを履いた女性（別に男性でも構わないが…）の下着が見えてしまうかあるいは見えないのかを、女性達が履くミニスカートの丈の長さから考察をしてみたのであった。

　その「ミニスカートの幾何学」の考察をした結果、ミニスカートの丈がちょうど32cmの時に、ミニスカートで下着が隠されはじめる境界線がちょうど階段と平行になる、ということが判ったのである。そして「下着が隠されはじめる境界線がちょうど階段と平行になる」結果、ミニスカートの丈が32cmより短いと下着が階段下を上る人達から見えてしまうようになり、逆にミニスカートが32cm以上の丈であればスカートの中の下着はなんと幸か不幸か見えることはないのだ、ということが判ったのである。ミニスカートをはいた女子高生が急な駅の階段なんかを上るときでも、ミニスカートの丈が32cm以上であれば、パンチラの恐怖に怯える必要はないということが判ったのであった。


　ところで、ミニスカートの中が見えてしまいそうになる場所というのは、必ずしも急な階段だけではないらしい。最近の東京の有名スポットなどでは、「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかがたくさんあったりするというのである。そして、そんな場所では、真上にいる「スカートを履いた女性」を急角度で仰ぎ見ることができて、スカートの中の下着がチラリと見えてしまうことがあるというのである。

　しかし、である。角度的にスカートの中の下着が見えるからといって、果たして本当に下着が見えるものなのだろうか？角度的には見えるはずでも、実際には人間の目には見えないことだってあるのではないだろうか。なぜなら、スカートが「私たちの視線から下着が見えるのを遮っている」のと同じように、スカートは「照明の光が下着にあたるのをも遮っている」のである。スカートの中というのはスカートに光が遮られて（たぶん）かなり暗いハズなのである。いや、実際に覗いてみた経験があるわけでは決してないので自信を持って「ハズ」と断言することはできないのだけれど、スカートの中が明るいわけはないと思うのである。もし、スカートの中が明るくなければ、仮にその中身を覗くことはできても結局暗くて何も見えないわけで、「スカートの中が（見えるくらいに）十分に明るいかどうか」が肝心だと思うのである。そこで、今回は「下着が角度的に見通せる条件」ではなくて、「スカートの中の下着が十分明るく見える条件」を考えてみたい。


　まずは、スカートをはいた女性を下の図のように簡単に示してみよう。スカートを下向きに開いた円錐として考えてみる。もちろん、スカートの中の下着はこの円錐の頂点に位置するわけだ。そして、スカートが広がる角度をΘとでもしてみることにしよう。その時、円錐の頂点にはどれだけの光が当たるものだろうか？

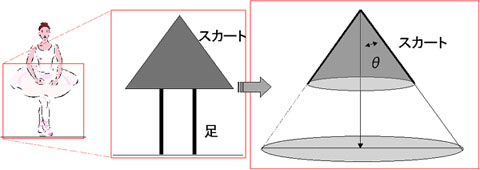　もちろん、円錐状のスカートが上からの光は遮っているわけだから、スカートの中の下着を照らす光というのは、下の床からの反射光だけである。つまりは、上の図で、「色を付けた部分の床」からの反射光のみが下着にまでたどり着き、それ以外の床からの反射光はスカートに遮られて、スカートの中を照らすことはない。ということは、「スカートの中はどれくらい明るいか？」という疑問を考えることは、それは「色を付けた部分の床からスカートの中の下着にまでたどり着く光がどれだけあるか？」ということを考えることと同じなのである。

　そしてまた、床上での光の反射に方向性が無く、光が完全に等方的に周囲に拡散するとするならば、円錐の中心（つまりはスカートの中の下着部分だ）にあたる光の量は、下の左図の色を付けた部分球の面積に比例する。つまり、「スカートの中の明るさ」は「スカートの広がり角」で決められる「部分球」の面積に比例するのである。


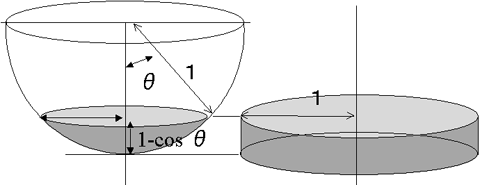　つまり、角度Θで広がるスカートの中が「どれくらい明るいか？」という疑問は、「下図で色を付けた部分球の面積はどのくらいか？」という問題に変わるわけである。「半球全体の面積に対して、スカートの広がりで決められる部分球の面積はどのくらいの割合か？」ということの答えが、それすなわち「スカートの中の明るさ」を決めているのである。

　ところで、アルキメデスが発見したように、球（もしくはその一部）の面積はその球に外接する円筒の面積に等しい。つまり、上の図の左で色を付けた部分の面積というのは、右に示したような（色を付けた）円筒の面積に等しいわけだ。ということは、右の円筒部分の面積は

円筒の面積 = 2 π (1-cosΘ)

であって、左の半球の面積が(直径=1とすると)2πだから、円錐状のスカートの中の明るさは、スカートの広がる角度をΘとするならば、「スカートの中の明るさ」は

という実に簡単な式で表されることになる。アルキメデスも、まさか自分の球と円筒の表面積に関する発見が「スカートの中の明るさを示す式（ここでは仮に『パンチラの式』とでも呼ぶことにする）」を導くために使われるとは想像だにしなかっただろうと思うが、とにかくアルキメデスのおかげで私たちはスカートの中の明るさを知ることができるのである。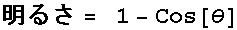

　試しに、このくアルキメデスの『パンチラの式』を使って、スカートの広がり角度Θに対して、スカートの中の明るさがどのように変化するかを計算してみると、その結果は下のグラフのようになる。このグラフは、横軸が「スカートの広がる角度」で、縦軸が「スカートの中の明るさ」を示している。周囲の「照明に照らされている床」の明るさを１とした時の「スカートの中の明るさ」を示しているのである。

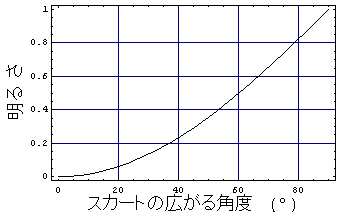　基本的にはスカートが広がるにつれて「スカートの中の明るさ」は明るくなるわけであるが、このグラフを眺めてみると、スカートの広がる角度が20°を超えるあたりから次第にスカートの中が明るくなることが判るだろう。例えば、スカートの広がる角度が30°の時には、スカートの中は「床の明るさの10%程度の明るさ」しかないが、スカートの広がる角度が60°にまで広がれば、スカートの中は「床の明るさの半分程度の明るさ」になる、ということが判るわけだ。


　ところで、人間の目というものは「見るものの明るさ」に合わせて順応する。例えば、暗いものを見るときには目の感度は自動的に上がる。だから、スカートの中がほのかでも明るかったならば（例えば床の明るさの5%程度にでも明るければ）、自動的にその明るさに目が順応してスカートの中が見えてしまうかと思いきやそうはいかない（ハズだ）。なぜなら、人間の目は明るいものを見る時には、目の感度が逆に自動的に低下してしまうからである。スカートの中以外の明るい場所（例えば照明や、照明に照らされた明るい壁）だって、自動的に視界の中に入ってくるわけで、目の感度はそういう明るい部分に自動的に合ってしまうハズなのである。

　例えば、下の画像は周りの明るさに対して、

1. 5%の明るさ
2. 10%の明るさ
3. 20%の明るさ

を持つ三種類のロゴである。この三つの画像を眺めてみれば、明るさが5%のものはなかなか判別しにくいが、20%以上の明るさのものであれば比較的容易に判別できることが判るだろう。明るいものが視野に入っている限りは、人間の目は「一番明るいものの10%以下程度の明るさのモノ」はなかなか識別することはできないのである。

5 %

10 %

20 %

　ということは、先のグラフで「スカートの中の明るさ」が10%を超えていないと、つまりは周囲にある明るい床（や照明や壁）などの明るさの10%を超えているくらいでないと、スカートの中が仮に幾何学配置的に見える条件であったとしても、実際には目の感度的にその中のようすを判別することができないに違いないのである。その場合、おそらく明るい床や壁の明るさに目の感度が合ってしまい、ほの暗いはずのスカートの中は真っ暗にしか見えず、幸か不幸かスカートの中身は識別することができないハズなのだ。

　というわけで、先ほどのグラフに「識別できる明るさか否か」を書き入れてみると、次のグラフのようになる。

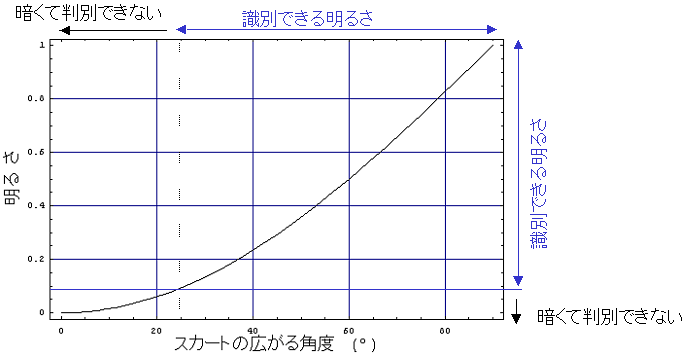　つまり、スカートの広がる角度が25-30°を超えていないと、スカートの中身は周囲の床や壁の明るさに比べて相対的に暗すぎて人間の目ではおそらく見ることができないのだ。


　例えば、スカートの広がる角度が30°以下に制限されるようなタイトスカートを穿いて、明るい壁や照明などが視界にどうしても入ってしまうような場所にたたずんでいる限りは、もし仮にスカートの中を覗かれたとしてもスカートの中は（人間の目からすると）真っ暗で何も見えないわけで、スカートの中身を見られたりするような被害にあうことはまずないだろう、ということが先のアルキメデスの『パンチラの式』から判るわけなのである。「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかであったとしても、背後に明るく輝くものがある限りには、見る人の目を眩ませることができて、スカートの中身は安全なわけである。

　ところが逆に、床が白かったりして明るいクセ（つまり下からの照明が強いクセ）に、周りに明るい壁や照明が何故かあまりないような場所がもしあったとして、もしそんな場所で（下から）スカートの中を覗かれたりしてしまうと、（下から覗く人の視界に入る）周囲の明るさに比べてスカートの中が十分明るく見えるせいで、しっかりとパンツの模様をチェックされてしまうということになるだろう、ということも予想することができてしまうのである。だから、そんな場所をもしも短いスカートをはいて歩かなければならないような場合には、例えば何かの「ピッカピッカ輝く光りモノ」でも身につけて、その光りモノの明るさを「スカートの中身をのぞこうとするスナイパー」の視界に入れて、彼らの目を眩ませてしまえば良いだろう、というアルキメデスの知恵さえ授けてくれるのだ。

　
　ところで、今回は「スカートの中の明るさを示す＝パンチラの式」を考えてみたわけであるが、この式は考えるまでもなく実にアブナイ式である。パンチラの被害防止に役に立ちそうな気もするし（全然役に立たないような気もするが）、逆に単なる「パンチラの科学」になってしまっているような気もしてしまう。「スカートの中身をのぞこうとするスナイパー」の魔の手から逃げるためのバイブルになるような気もするし、「スナイパー」のための手引き書になってしまいそうな気もする。ギリシャ神話で、あらゆる災厄が入っていたという箱がパンドラの箱だったけれど、このパンチラの式だって案外そんなパンドラの箱のような、色んな災厄の元になってしまうものかもしれないのである。しかも、パンドラの箱の場合には最後に箱の中に『希望』が残っていたわけでまだ良い（？）のである。しかし、アルキメデスの『パンチラの式』の場合には「スカートの中にだっては『希望』が入っているのだぁ」などと口に出したりしたら単に変態扱いされてしまうだけなわけで、そこはパンドラの箱よりもずっとたちが悪いのである。つまりは、科学もアルキメデスの『パンチラの式』も使う人次第なのである。

■美人の微分方程式　

あなたの写真を美人にしよう

　ここで作成したソフトのオンラインバージョンが作成されています。

---

あなたの写真を美人にしよう

　先日、ブサイク・フィルタという面白いソフトウェアを知った。それが一体どういうものかというと、なんと画像の微分成分を原画像に足すことで「どんな美人もブサイクにしてしまう」という画像処理ソフトなのである。何が美しく何がブサイクか、というのは人間の感性の問題でもあるし、そんな美醜を機械が処理するのは難しそうに思えるだろう。しかし、実際にブサイク・フィルタのアプリケーションで処理を行ってみると、下に示した例で判るように、確かに「美人がほどよくブサイクになってしまっている」ことが判る

原画像

「ブサイク」処理後

　このフィルタは一体どうやって美女をブサイク化しているのだろう？と不思議に思いながら、ブサイク・フィルタの説明書を読んでみると、そこには
という式で処理をしている、と書いてある。通常、スケッチ風にしようとして微分することはあるが、それでブサイクな感じも得られるというのはちょっと新鮮だなぁと思っていると、前後して
なんていう質問メールを頂いた。なるほど、確かに
という方程式が成り立っているのであれば、この式を少し変形した
という方程式だって、成り立っているかもしれない。人を勝手に「ブサイク」にしてしまうフィルタも面白いが、人を勝手に「美人」にしてしまうフィルタだって同じように面白いかもしれない。しかも、面白いだけではなくて実用性もあるかもしれないということで、今回はこの「美人画像の微分方程式」について考えてみることにした。

　まずは、
という式により行われている処理がどのようなものであるかを考えてみよう。これは「微分成分」が、明るいところと暗いところの境界部で大きくなるものであって、それを原画像の輝度値に足している（明るくする）と言うことから、結局、行われていることは「明るいところと暗いところの境界線を明るくする」という処理であることがわかる。

　そして、人間の顔の中では
であることから、この式は結局のところ「目や口の境界部を明るくする」という処理を行っていることになる。そして「目や口の境界部を明るくする」と、つまるところ「目や口が小さく見える」ということになる。「大きな瞳を持つ」ということは美人であるための大きな条件の一つだろうから、目が小さくなるということは、美人度が低くなり「ブサイク」になるというのはとても自然なわけである。これが
という「ブサイク」微分方程式の意味であるわけだ。

　そしてまた、逆に
という処理をすると、目や口を大きくはっきり描くことになり、結果としてはきっと美人になるに違いないのである。だから、先のメールで指摘されていたように
という「美人」微分方程式が成り立つに違いない、ということになる。

　とはいえ、これだけでは単なる推論に過ぎないわけで、実際に試してみなければならないだろう。そこで、この

1. 「ブサイク」微分方程式
2. 「美人」微分方程式

の処理を行うアプリケーションとPhotoshopプラグインを試しに作ってみて、これらの微分方程式が成り立つかどうかの実験をしてみることにした。

　まずは、「ブサイク」微分方程式をもう一度確認してみよう。これはもちろん先のブサイク・フィルタと同じで確かに「目や口が小さくなって」原画像よりもブサイクになっていることがわかる。

原画像	「ブサイク」処理画像

　そして、次に「美人」微分方程式の処理を行ってみた。原画像が元々かなりの美人なので判りにくいとは思うが、「美人処理」を行ったものは確かに美人化されていることがわかる。どうやら、「美人」微分方程式は正しく成立しているようである。

原画像

「美人」処理画像

　そして、もっとわかりやすいように、先に作った「ブサイク」画像に対して「美人処理」をしてみたものが次のようになる。もともとの「ブサイク」原画像がずいぶんと美人化していることを確認できることと思う。

原画像（「ブサイク」）

「美人」処理画像

　ところで、今回考えてみた「美人」微分方程式は目の縁取りを行うことで目を大きく美人に見せることになるわけであるが、それは結局のところ女性の化粧と同じである。「目の回りにアイラインやらアイシャドーやらを入れて、目を大きく美人に見せる」ということを機械的にしているだけのことである。「ブサイク」微分方程式は女性の化粧を落とした顔を見せているのと同じ事であるし、「美人」微分方程式は女性に化粧をした顔を見せているのと同じことである。女性は化粧次第で変身するとよく言うが、今回の処理をいろんな人達にかけて、その処理前後の画像をじっくりと眺めることで、その人達の化粧前後の顔を想像してみるのも面白いかもしれない。あるいは、あなたの写真を（もっと）美人にしてみるのも面白いかもしれない。

■オトナとコドモの境界線　

　オトナとコドモの境界線をひくとしたら何処に一体ひくだろう。十五才？二十才？それとも三十才？あるいは、人によっては自分より下がコドモで自分より上がオトナなんて線をひいてしまうだろうか？そもそもコドモって何だろう。きっと、それは単に「オトナになってない状態」のことだろう。だとしたら、オトナって一体何なのだろうか？

　じゃぁ、というわけでまたもや新明解のページを眺めてみることにした。

自覚・自活能力も持ち、社会の裏表も少しずつ判りかけてきた人

　なるほど、「社会の裏表も少しずつ判りかけてきた人」がオトナなのである。しみじみと深い言葉なのである。何より先に「社会には裏表がある」という言い切ってしまうところがまさに新明解なのだ。新明解はきっと苦労を知っているのである。
　そして、ここでいう「裏」とは、きっとネットランナーに掲載されるような「裏ツール」などで使われる薄っぺらい「裏」という言葉とは次元の違うものに違いない、と思うのである。コドモが思う「裏」とオトナの思う「裏」とは世界がきっと違って、きっと「映画のセットの裏」と「現実の街角の裏」くらい違うものじゃないだろか、と思うのである。

　それにしても、オトナとコドモの境界線って一体どこにあるんだろう。

■集合とその補集合の境界線をひく、ということ　

　センのパラドックスは、言い換えれば「万人に奉仕する社会はどうやっても作り得ず、一部の人間にとっての社会しか作り得ない」ということなのだろうか。そして「一部の人間」と「その補集合」を区切る絶対的な線を引くことはできず、誰かが…

というおれカネゴンの「算数記」の文を読んでから、「センのパラドックス」を説明する『合理的な愚か者』へ。

　定義域の非限定性（＝どんな変なヤツもいるような社会？）であれば、「リベラル」的かつパレート的な（＝どいつのわがままも聞きながら、みんなが満足するような？）社会決定はできない

というその証明の解説は「はてなダイアリー」の「はてなダイアリー評議会」などの一連の動きを連想させ、さらに集合Aの補集合のさらにその補集合がその集合Aだと、なんとも当たり前のこともふと考えさせられる。集合Aになれなかったものがその補集合なのか、それともその補集合になれなかったものこそが集合Aなのか、消去法で決まる側はどちらなのか、とふと考える【補集合の補集合とはおれカネゴン】。