1999-08-08[n年前へ]
■瞳の中の真実 
目の屈折率を調べよう
先日、近所の海へ行ってきた。水中メガネで覗いているとまるで熱帯魚みたいな魚が泳いでいて素敵なのだ。水中メガネを使うか使わないかで、海の楽しさは雲泥の差である。水中メガネで覗いてみると、裸眼の時とは別世界のようにくっきり見えるのである。
 |
さて、「水中視の光学」と言えば、物理の散歩道の「アユと泳ぐ」(新物理の散歩道-第2集- 中央公論社)に詳しく面白い考察がされている。本WEBでもScrapsにて「焦点」ということを考えたばかりなので、「アユと泳ぐ」と同様の解析を「できるかな?」風に行ってみたい。光学シミュレーターを作ってみたいのである。そのために、まずは人間の目の中の屈折率を調べなければならないだろう。というわけで、今回は下調べ編である。
それでは、人間の左目の水平方向の断面図を調べてみる。
 |
この中で普通のカメラでいうレンズの役割を果たしているのはどこだろうか。レンズの部分を赤く塗るとどのようになるだろうか?下に並べた3つのうちどれだと思われるだろうか。
A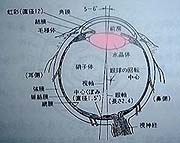 | B | C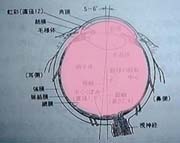 |
まずは、目の中の物質の屈折率を調べてみると、以下のようになる。
| 場所 | 屈折率 |
| 角膜 | 1.376 |
| 眼房 | 1.336 |
| 水晶体 | 1.386 |
| 硝子体 | 1.336 |
空気(15℃の乾燥空気)の屈折率はほぼ1.0であるから、空気と比較するならば、目の中の物質はほぼ同じ屈折率を持つといっても良い。角膜も眼房も水晶体も硝子体も同じ屈折率を持つとして良いだろう。すなわち、大雑把な近似においては図.2のCに示したようなピンク色のレンズがあるとして良い。つまり、目全体がレンズであり、レンズ面に焦点を結ぶようになっているのである。水晶体は若干の補正を行うに過ぎない。レンズの焦点はレンズから離れた場所にあるはずと思っている人もいるかもしれないが、レンズの表面に焦点があるものも実はよく使われている。
さて、人間が水の中に入るとどうなるだろうか?水は1.333(589.3nmの波長の光に対して)の屈折率を持つ。これは人間の目の中の物質の屈折率とほぼ同じである。水を主体として出来ている人間なのだからこれは当然だろう。しかしこれでは、目は光を屈折させることはほとんどできなくなる。そのため、水の中に入るときには水中メガネなどで目の回りを空気で満たしてやることが必要なのである。
本題からははずれるが、資料を眺めていると、面白いグラフが目に入ってきた。人間の目の断面方向の視細胞個数の分布を示したものであり、錐体と桿体を個別に示してある。「盲点」なんかも図中にある。
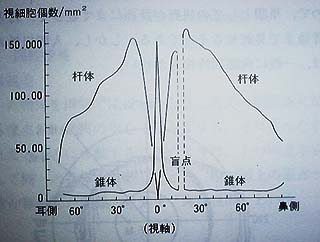 |
目に映る明るさって何ですか? - 君は天然色 - (1999.07.05)
の回に錐体と桿体については触れたが、桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上で働く。従って暗いものを見るには桿体の働きが重要になるわけだが、上のグラフは桿体が視点の中心にはほとんど存在していないことを示している。
従って、暗い所でものを見る際には、視点の中心では感度が足りなくなりやすいことがわかる。これまで、暗い星を眺めるときに視界の中心で見ようとすると見えないのだが、少し視点をずらしてやると見えるような気がしていたのだが、それは気のせいでは無かったようである。
さてさて、資料集めも終わったので「瞳シミュレーションソフトウェア」の開発に着手したいと思う。もちろん、時間がかかるのはいつものことだ。すぐにはできないけどね。
1999-09-23[n年前へ]
■MiosoftはApple株でいくら儲けているか? 
価値観は線形なままで
ユング心理学では因果関係が無い偶然の一致を「シンクロニシティ(共時性)」と呼ぶ。いろいろ意見の違いもあるだろうが、私は「シンクロニシティ(共時性)」は結局偶然のせいではなく、世の中の流れの要請による必然なのではないかと思うのである。
と、いきなり訳のわからない話だが、今回の話は「今日の必ずトクする一言」の
ともあれ、webmaster氏のメールのおかげで、株価の値軸が妙に頭に残る最中に、私は「MicrosoftはApple株でいくら儲けているか?」という疑問が沸いて、Appleの株価を見に行ったのである。何しろ、MicrosoftはAppleの大株主である。
 |  |
一見似ているように思える。しかし、よく見てみると軸が違っている。左のAppleComputerの株価変動は対数軸で表されている。「株価表示グラフで値の軸を対数軸にできないか」という言葉が頭にあったせいで気づいたわけだ。そこで、この違いが新鮮で「今日の必ずトクする一言」のwebmaster氏への返信に至ったわけである。
それでは、左のAppleComputerの株価変動をリニアな軸に変換してみよう。
 |  |
印象が全く違う。右の線形軸のグラフは値軸の間隔が等間隔になっているのがわかると思う。それに対して対数軸で表されている右側は上に行くほど間隔が短い。右の線形軸では株価が急激に上昇しているのが実感できる(私は)。株取引的な考察は「対数軸証券グラフのナゾ」の方にあるので、ここでは本題の「MicrosoftはApple株でいくら儲けているか?」に戻る。
さて、このグラフのようにApple株は急上昇中なわけで、問題の「MicrosoftはApple株でいくら儲けているか?」であるが、97/08/08当時の13ドル前後の株価で一億五千万ドル分のApple株を買っていたとしたら、現在は80ドルくらいであるから、およそ6倍。すなわち、一億五千万ドルから九億ドルになっていることになる。うーん、たまらん。800億円近い差が有る(線形的な発想)。
さて、最初の疑問はこれで解決したのだが、わが「できるかな?」でも株価の軸の
- 対数軸
- 線形軸
日頃、実験を行っている時などは
「たかだか一桁の変化だろう。」などと対数軸の感覚に支配されているのであるが、こと経済になると線形軸の感覚に支配されるのである。これは私が貧乏であるからかもしれない。1万円はどんなときも1万円なのである。10万円と11万円の違いも、100万円と101万円の違いも同じなのだ。これが一億円と一億一万円でも同じである。何しろ、そんなお金と無縁なのである。であるから、貧乏な金銭感覚をそのまま線形で延長してしまうのである。「金銭に関する差の感覚」といってもよい。
これは人によっても違うだろう。私と違うブルジョアジーな人であれば、例えば、車を買うときに
「300万円の車を買うから、30万円のカーナビを一緒に買っても誤差みたいなものだ。」という人もいると思う。また、「一億円と一億一万円は同じだ」と言うだろう。これなどは経済に関する対数軸の感覚の一種だと思う。この人は「金銭に関する比の感覚」を持つ人である
さて、こういうことを考えていくと、金持ちの1万円と私の1万円は価値が違うことにいまさらながら気づくのである。私は1万円もらったら大喜びだ。しかし、同じだけビル・ゲイツを喜ばせようと思ったら、九億ドル位は必要だろう。そういうことを考えると、経済社会は実に対数軸である。いや、むしろ世の中が対数軸だと言ったほうが良いだろうか?
今回の話とやはり似て非なる話がロゲリギストの「第四物理の散歩道」の「理解の形式」に述べられているので、興味の有る方は読むと面白いと思う。
さてさて、同じ題材をとってみても経済オンチの私が作る「できるかな?」は「「対数軸株価グラフのナゾ」」とは違い、ずいぶんと変な話になってしまったようである。しかし、それが個性というもの。みんなが同じではつまらない。
ともあれ、価値観に対する評価軸は線形軸の方が良い、と思う私であった。
1999-12-30[n年前へ]
■6502と並列計算とムーアの法則 
人間のクロック&スケールアップ
「物理の散歩道」を読み直していると、とある文章に興味を覚えた。
- 第五物理の散歩道 ロゲルギスト著 岩波新書
「通信を考える」の中の興味を惹かれた部分は「信号の伝わる速度と距離と処理速度の関係」を論じている部分だ。例えば、計算機は処理速度を高めるためには回路の大きさを小さくしなければならないとか、人間の頭脳の働きの速さから集団生活の広がりの限界について論じているのだ。例えば、
- 計算機の演算速度の時間スケール -> ナノ秒 = 10^-9s (クロックで考えると、1GHz)
- 人間の演算速度の時間スケール -> サブ秒 = 10^-1s (クロックで考えると、10Hz)
つまり、通信の速度が光速度であるとして、演算の単位クロックの間に通信が行われなければならないとするならば、計算機の時間・空間スケールと人間の時間・空間スケールは等しいだろう、という推論だ。
そして、さらにロゲルギストの想像は広がり、並列計算についても論じている。
計算機が東京と大阪に離れて置かれていて、通信をしながら作業をするとしたら、人間の場合にはそれと同じ条件というのはどんなものだろうか、と彼らは考える。それは、光の速度で55時間、ちょうど冥王星の軌道直径の5倍程度の空間スケールになる、と論じている。それ以上、離れた場合には演算の過程を共に行うのは無理ではないかというのである。
こういう文章を読んでいると、この文章が作られたのが30年以上前であることを忘れてしまいそうである。この人達の思索の自由さに憧れを感じてしまう。この人達は、頭の中にタイムマシンにでも持っているのだろうか、と感じてしまうのだ。
ところで、私がコンピューターをいじるようになった頃は、Apple][の時代だった。といっても、私はお金があふれていたわけではないので、XXX電子でAplle][のコンパチ基盤を買って組み立てて使っていた。その基盤上の6502は1MHzで動いていた筈だ(あぁ、I/Oの6809派vs6502派の論争が懐かしい!)。
それから20年程たち、CPUのクロックスピードは1GHzを越えようとしている。20年で1000倍である。そして、その集積度は、ムーア(GordonMoore)の法則の「半導体の性能と集積は、18ヶ月ごとに2倍になる」に従っている。
それでは、人間はどうだろうか?人間の脳味噌のクロックがどの程度であるか測定されているかどうか、素人の私にはよくわからない。しかし、WEB上のデータとしては、例えば
- Mayo's Profile( http://www.ceres.dti.ne.jp/~mayo/profile.html )
ロゲルギストの時代、すなわち30年以上前、から現在のMayo's Profileの値がほとんど変わっていないように、人間の演算スピードは変わるようなものではない。それは、そうだろう。ヒトのクロックスピードや集積度といったものは、変えるわけにはいかない。当然である。CPUと違ってプロセスルールを変化させるというような訳にはいかないのだ。
それでは、演算性能を上げようとしたらどうするだろうか?そうなると、並列計算を行うのが自然だろう。単独のCPUの性能を上げるわけに行かなくても、共同作業を行えば、演算性能を上げることができる。
現代はほとんどの作業が共同作業で行われる。また、その共同作業も大人数が関わるようになってきている。それは、どんな業種でも同じだ。一人では、なかなかできないことが多くなっている。
それら共同作業、すなわち並列計算、を行う人達(例えれば並列計算機における各ノード)を増やし、それらの間の情報転送をすばやく行うことが多くの作業(計算)を行うための手順だろう。
そこで、
で用いた- 人口増加( http://www.t3.rim.or.jp/~kabutoya/KABHTML/Yoi/2-1.html )
 |
なるほど、人間界の並列計算機におけるノード数は増加している。そして、各ノード間の通信速度を調べるために、まずは、
- 来て、見て、触って、情報伝達
- ( http://www.f-jhs.fukuoka-edu.ac.jp/3-3/jyoho.html )
西暦 内容これを全部転送速度に直してみる。といっても、よくわからない部分も多いので、私が適当に決めてみる。それでは、その変化を示してみよう。とりあえず、ここ200年位の間のものを考える。
-4000 のろし
-2400 伝書鳩
-2300 馬による伝令制度
1837 モールス電信機
1876 ベグラハム=ベル電話機
1909 グリエルモ=マルコーン無線電話機
1973 Ethernet XeroxPARCで生まれる。(ちなみにEther=エーテル)
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
西暦 内容という感じだ。グラフにすると、
1837 モールス電信機 = 2bps
1909 グリエルモ=マルコーン無線電話機=10kbps
1979 DIX規格=10Mbps
1992 FastEthernet=100Mbps
 |
こんな感じである。対数グラフにおいて直線的に情報伝送速度が速くなっている。この関係は結構きれいである。
別に意図してこういう数字にした訳ではないのだが、不思議なことである。
このようにして、人間(ノード)間の転送レートが高くなることにより、先のような人口増加に伴うトラフィック増加をしのぐことができていると考えることもできるかもしれない。そして、人間達の共同作業、すなわち並列計算、を行うだけのバススピードを確保しているのである。
最近、会社組織などで分社化とか事業分割とかの話題をよく耳にする。こういった時に、分割における時間と空間のスケールはよく考える必要があるだろう。分割が有効なのは、ほとんど独立なものを分割する場合のみである。並列計算における領域分割などと同じだ。
共同作業がほとんどなく、結果のみをやりとりすれば良いような場合には分割による効果はあるだろう。その一方で、同じ事業・作業を行っているところが、離れていては作業の効率は上がらない。もし、技術系の会社でそのようなことを行うのであれば、事業や部署を並列化した際の真面目なシミュレーション位は行うべきだろう。いや、別に深い意図はないけど。
こういったことは「新・闘わないプログラマ No.109 時代錯誤」に書かれていることとも少し似ているような気がする。
さて、1999/12/30-2000/1/1は野沢温泉で温泉&スキーである。2000年問題で会社に泊まり込む人も多いが、私はスキー場で泊まり込みである。同時期に野沢温泉に行く人がいるならば、ぜひ一緒に「スキー場の特殊相対性理論」について討論したいと思う(スキー場で)。
2000-01-08[n年前へ]
■着メロの音響工学 
この着信音は誰のだ!? 立体音感その3
街中で携帯電話の着信音が鳴ると、周辺の人が一斉に自分のポケットを探る光景というのはよく見掛ける。それは、まるで「クイズ・ドレミファドン」のようである。そう「超・イントロクイズ」そのものなのだ。「このイントロはオレのか!?それとも!?」と皆が考えている瞬間である。
着メロのイントロが始まるや否や、腰の携帯電話に手をやる様子は「おまえは荒野のガンマンか!」とツッコみたくなる程である。
特に、私の勤務先などでは全員が同じPHSを持ち歩いているせいか、着信音が聞こえ始めると、みな自分のポケットを探り始める。もちろん、そのPHSの着信音は数種類ある。しかし、1500人程度の従業員がいるわけだから、1500人/ 数種類だけ同じ着信音があるわけだ。仮に15種類あるとしても、
1500(人) / 15(種類数) = 100(人/種類)つまり、自分と全く同じ着信音のPHSを持つ人が100人もいるのだ。世の中には「自分と同じ顔の人が七人いる」というが、職場に同じ着信音の人が100人もいるのである。これでは、着信音が鳴ると同時に多くの人がポケットを探るのも自然だろう。
もちろん、この解決策として、「着信音でなくてバイブレーターを使う」というものがあるわけだが、何故かその解決策は許されないらしい。不思議である。
さて、そもそも、何故自分の着信音を区別できないのだろうか? まず、その辺りから考えてみることにする。
着信音が鳴ったときに、「自分の着信音かどうか判断するための基準」は二つあるだろう。それは、
- 着信音の種類
- 着信音が鳴っている位置
着信音の鳴っている位置 = 自分の携帯電話の位置が成立するかどうか即座に判断できれば、着信音が同じでも「自分の着信音であるか」の判断が可能ということだ。
つまりは、「携帯電話の着信音という音源の定位」という問題を考えれば良いことになる。もし、「着信音の定位」が判れば、自分の携帯電話の着信音か他の人の着信音かどうかなんてことは考えなくて済むのだ。そう、今回は「立体音感」シリーズその3だったのである。
それでは、一体「着信音がどこで鳴っているのか、すなわち、着信音の定位」が判るためには何が必要なのだろうか?
前回、
で「音の立体感に関する因子」について- 音像定位の因子
- 両耳差因子 (音響信号)
- 音の強さ(振幅)の差
- 位相の差
- 周波数スペクトル因子
周波数スペクトル因子というのは、例えば、
の中の記述指を前方で鳴らしてみて下さい。 そしてすこしずつ手を頭の側方に、手と頭の距離を変えないようにして、移動してみて下さい。 音量がわずかに大きくなったこととある特定の中域および広域の音がより強調されることに気が付かれるでしょう。 この実験では、指を鳴らす動作は一定の音量と周波数を発生する音源として用いられたわけです。 耳は同一の音源が前方から来る場合と、側方から来る場合で全く違う音と聞き分け、頭脳にそれを登録します。 側方の音は若干大きく、また耳たぶのせいで高い周波数で聞こえます。にあるようなものである。
音波が人間の頭部を通過してくる間に音波の周波数分布が変化し、その変化具合で音波がやってきた方向を知ることができるというものだ(多分)。もちろん、位相分布も変化するだろうが、ここでは周波数分布しか考えない。
こういう音像定位の因子における「周波数スペクトル因子」を考える時に、もし音源の周波数スペクトルがごく狭いものだったらどうだろうか?つまり、単一の周波数しか含まない音源だったらどうだろうか?周波数スペクトルが変化するといっても、単一のスペクトルしか含んでいないのだから、振幅が変化する効果しかない。周波数スペクトルの分布は何ら変化しない。
ということは、「音像定位の因子における周波数スペクトル因子」が上手く作用しないことになってしまう。(もちろん、実際には非線形な効果が存在するだろうから、多少は周波数スペクトルも変化するとは思うが。)
これと全く同じことはまたしても「物理の散歩道」で触れられている。ロゲルギスト著の岩波新書「第四物理の散歩道」の「不規則なものの効用 三節」である。純音より不規則な音の方が「立体感」を得られるだろう、と書いている。
今回、「携帯電話の着信音の定位」を「着信音のスペクトル分布」という観点から調べてみることにする。携帯電話の着信音がどのような波形であるか、どのような周波数分布を持っているかを調べるのである。果たして、携帯電話の着信音の周波数分布はどうなっているのだろうか?(部品点数を考えれば、ほぼSin波か矩形波なのが当然だろうが...)
まずは手持ちの機種で着信音の波形とスペクトルを見てみることにした。使った機種を以下に示す。
 |
それでは、着信音No4と着メロ「この木何の木」の波形とスペクトログラムを次に示す。それぞれのグラフ中で上は「時間vs周波数分布」を示すスペクトログラムであり、下は「時間vs強度」の波形グラフである。
まずこれが、着信音No.4の波形とスペクトログラムであり、
 |
こちらが、「この木何の木」の波形とスペクトログラムだ。
 |
どちらも周波数分布はそれほどブロードではない。すると、「音像定位の因子における周波数スペクトル因子」を用いた「立体音感」がうまく働かないかもしれない。ただし、着信音No.4に関しては時間的に変化しないが、着メロ「この木何の木」に関しては、当然だが時間的に変化していく。
この違いが果たして、「着信音の音像の定位」の判断を左右するものか、自分の耳で実験することにした。着信音No.4と着メロ「この木何の木」を鳴らした時に、どこから鳴っているように聞こえるか判断してみるのだ。
目をつぶり頭の周囲で着信音を鳴らし、その定位を判断してみた。すると、色々な着信音を聞いてみたがいずれも定位の判断がしづらかった。特に頭の前後の判断がしづらい。それは、着信音No.4と着メロ「この木何の木」でも同様であった。やはり、純音に近いと「音像定位の因子における周波数スペクトル因子」が働きづらいのかもしれない。
そして、着信音No.4と着メロ「この木何の木」だが、むしろ着信音No.4の方が判断をしやすかった。メロディだと音が変わるときに定位が変わるかのような感覚を受けた。そのため、判断をしにくかった。もちろん、これは私だけの感覚かもしれない。その辺りは被験者を増やして実験をしてみたい(再実験をする日が来るかどうかは大いに疑問であるが)。
また、もしかしたら着信音No.4の方が矩形波に近く、純音でないのが良かったのかもしれない。もしかしたら、の話だけれど。
もし、今回使った音を聞いてみたい人がいるならば、
これを聞いてみてもらいたい。ただし、サイズがでかいので要注意だ。あとバックグラウンドがうるさいのはハードディスクとファンの回転音である。困ったものだ。 最近多い「同時発声数が多い着メロ機能」というのも、使って実験すると面白そうだ。しかも、音が分厚いヤツがあると、案外良いモノかもしれないな、とうらやましく思ったりするのである。そして、着信音スピーカーがプアァで歪んでいる機種なんかが、色々な周波数成分を含んでいて、実は「着信音の定位」に関しては良かったりするのかもしれない、と考えたりする。しかし、こちらはチットモうらやましくないのであった。
2000-01-21[n年前へ]
■数字文字の画像学 
縦書きと横書きのバーコード
始まりはまたしても「物理の散歩道」である。
- 「新物理の散歩道」 第一集 ロゲルギスト 中央公論社
さて、その中の-横組・縦組と二つの目-という一節中の外山滋比古氏の発言が実に面白い。
「日本の漢字は横の線が発達してますから、横から読みますと目に抵抗が少なくて読みにくいですね。ヨーロッパの文字は縦の線が非常に発達していて、横に読むと非常に能率がいいわけです。数字でも縦の棒を引いて、Ⅰ、Ⅱ、Ⅲ、Ⅳ....としますが、和数字は横に線を引いて一、二、三...となります。...」という発言である。
- 文字は読む方向に対して垂直な線が多い
- また、読む方向に対して水平な線は少ない
- いずれも目のスキャン方向に対して垂直な線が多い
そこで、今回その確認と考察を行ってみることにした。サンプルとしては、外山滋比古氏の発言の通り、ローマ数字と漢字数字を用いることにする。
まずは、本来の書き方の方向に数字を並べた画像である。画像サイズは128x128である。後の処理のために、縦横比を同じにした。すなわち、本来の画像のアスペクト比とは異なる。
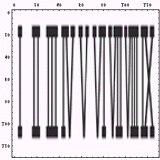 |  |
この二つの画像を読む方向に目を走らせると、まるでバーコードのようである。以前、
の時に作った郵便カスタマバーコードを参考に示してみる。考えてみると、バーコードは検出手段をバーコードの進行方向に走らせて、情報を読み取るわけである。人間が数字の羅列を読み取るのも、数字文字列上に目を走らせるのであるからまったくもって同じである。
一次元バーコードを考えた時、バーコードのバーは進行方向に対して垂直なものがほとんどである(若干のアジマス角を持つものもあるが)。バーコードを読み取る方向に対してのみ情報が書き込まれているのだから、それ以外の方向には等方的であるのが当然である。もし、そうでなかったらスキャン位置がちょっとずれただけでデータの読み取りができなくなってしまう。
そう考えると、先の数字文字に関する
- 読む方向に対して垂直な線が多い
- 読む方向に対して水平な線は少ない
また、本来の数字文字を並べる方向が読み書きの方向と異なる場合を以下に示す。
 |  |
さて、画像を並べるだけではつまらないので、
- 本来の書き(並べ)方
- 本来の書き方と異なる書き(並べ)方
人間の目が数字文字列上をスキャンしていくときに、選られる情報量を考えるために、読む方向に対して画像を微分したものを示す。もう少し正確に言えば、微分値の絶対値を画像にしたものである。
まずは、本来の書き(並べ)方のものを示す。
 818892 |  923836 |
微分画像の下に示した数字は微分(して絶対値)画像のピクセルの値の総和である。これをスキャン方向に対して選られる情報量の指標として扱うことにする。「スキャン方向に対して変化量が大きいということは、情報量が多い」ということだからである。
次に、本来の書き方と異なる書き方の場合を示す。
 536383 |  632338 |
それでは、「微分(して絶対値)画像のピクセルの値の総和」を比較してみることにしよう。
| 本来の書き方の場合 | 818892 | 923836 |
| 本来の書き方と異なる場合 | 536383 | 632338 |
ローマ数字、漢字数字の両方で、本来の書き方の方が(読む方向に対する)画像の変化量が大きいことがわかる。すなわち、「目のスキャン方向に対して選られる情報量」が多く、そうでない方向には冗長なのである。エラー発生率が小さくなるのである。本当にバーコードそのものである。文字はバーコードの祖先だったのである。
さて、「文字の画像学」も色々と面白そうなので、これからちょこちょこ遊んでいこうと思う。