1999-08-08[n年前へ]
■瞳の中の真実 
目の屈折率を調べよう
先日、近所の海へ行ってきた。水中メガネで覗いているとまるで熱帯魚みたいな魚が泳いでいて素敵なのだ。水中メガネを使うか使わないかで、海の楽しさは雲泥の差である。水中メガネで覗いてみると、裸眼の時とは別世界のようにくっきり見えるのである。
 |
さて、「水中視の光学」と言えば、物理の散歩道の「アユと泳ぐ」(新物理の散歩道-第2集- 中央公論社)に詳しく面白い考察がされている。本WEBでもScrapsにて「焦点」ということを考えたばかりなので、「アユと泳ぐ」と同様の解析を「できるかな?」風に行ってみたい。光学シミュレーターを作ってみたいのである。そのために、まずは人間の目の中の屈折率を調べなければならないだろう。というわけで、今回は下調べ編である。
それでは、人間の左目の水平方向の断面図を調べてみる。
 |
この中で普通のカメラでいうレンズの役割を果たしているのはどこだろうか。レンズの部分を赤く塗るとどのようになるだろうか?下に並べた3つのうちどれだと思われるだろうか。
A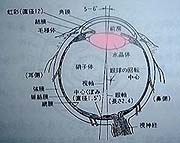 | B | C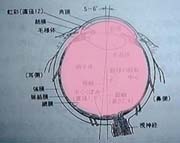 |
まずは、目の中の物質の屈折率を調べてみると、以下のようになる。
| 場所 | 屈折率 |
| 角膜 | 1.376 |
| 眼房 | 1.336 |
| 水晶体 | 1.386 |
| 硝子体 | 1.336 |
空気(15℃の乾燥空気)の屈折率はほぼ1.0であるから、空気と比較するならば、目の中の物質はほぼ同じ屈折率を持つといっても良い。角膜も眼房も水晶体も硝子体も同じ屈折率を持つとして良いだろう。すなわち、大雑把な近似においては図.2のCに示したようなピンク色のレンズがあるとして良い。つまり、目全体がレンズであり、レンズ面に焦点を結ぶようになっているのである。水晶体は若干の補正を行うに過ぎない。レンズの焦点はレンズから離れた場所にあるはずと思っている人もいるかもしれないが、レンズの表面に焦点があるものも実はよく使われている。
さて、人間が水の中に入るとどうなるだろうか?水は1.333(589.3nmの波長の光に対して)の屈折率を持つ。これは人間の目の中の物質の屈折率とほぼ同じである。水を主体として出来ている人間なのだからこれは当然だろう。しかしこれでは、目は光を屈折させることはほとんどできなくなる。そのため、水の中に入るときには水中メガネなどで目の回りを空気で満たしてやることが必要なのである。
本題からははずれるが、資料を眺めていると、面白いグラフが目に入ってきた。人間の目の断面方向の視細胞個数の分布を示したものであり、錐体と桿体を個別に示してある。「盲点」なんかも図中にある。
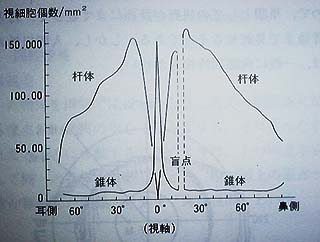 |
目に映る明るさって何ですか? - 君は天然色 - (1999.07.05)
の回に錐体と桿体については触れたが、桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上で働く。従って暗いものを見るには桿体の働きが重要になるわけだが、上のグラフは桿体が視点の中心にはほとんど存在していないことを示している。
従って、暗い所でものを見る際には、視点の中心では感度が足りなくなりやすいことがわかる。これまで、暗い星を眺めるときに視界の中心で見ようとすると見えないのだが、少し視点をずらしてやると見えるような気がしていたのだが、それは気のせいでは無かったようである。
さてさて、資料集めも終わったので「瞳シミュレーションソフトウェア」の開発に着手したいと思う。もちろん、時間がかかるのはいつものことだ。すぐにはできないけどね。
2000-03-29[n年前へ]
■明日、春が来たら 
風の中の瞳

昨日、海辺を歩いた。車は海沿いの堤防の上に停めた。堤防の上に留めた車の揺れが止まらない程、強い風が吹いていた。もう三月も終わりなので、春一番というわけではないだろう。それでも、もう春なのだなぁ、と強く感じさせる。
ところで、この海辺からは富士山がよく見える。富士山レーダーもよく見える。この海辺ももちろん見通しは良いのだが、「見通せる範囲」を言うなら、富士山レーダーの方がずっと広い。遠くを見通すのがレーダーの使命なのだから、当たり前の話だ。そして、富士山の山頂から、遙か遠くまで見通し続けたのが、富士山レーダーである。
今日、NHKの「挑戦者たち」でその建設をした人達が紹介されていた。富士山レーダーを作る指揮をし、情熱を傾けていたのが当時、気象庁観測部補佐官だった藤原寛人、すなわち、新田次郎であるとは知らなかった。新田次郎が富士山の山頂に行きたいから気象庁に入ったというのは、知っていたが、富士山レーダー建設の指揮をしていたとは知らなかった。とても面白く、そして何故か納得する話だ。
息子の藤原正彦もそうだが、新田次郎の書く文章には「冷静に見通す力」と「情熱」が同居している。時々、新技術を考えていると、彼らのような、未来すなわち明日を「見通す力」と「それを手に入れる情熱」が欲しい、とつくづく思う。
2001-02-11[n年前へ]
■もう一つの目から眺めた世界 
hirax.net式「平面画像立体化法」
先日、出張のついでに本屋で野田秀樹の「20世紀最後の戯曲集」を買った。電車の中で冒頭の「RightEye」を読んでいると、こんな台詞があった。
オレはもう二度と、立体写真を見ることができない。立体星座早見盤とか、アトラス立体地図とか、ああいうのが見れなくなるんだぞ。「Right Eye」は野田秀樹自身の右目失明、カンボジアで亡くなったカメラマン一ノ瀬泰造、被写体を執拗に追いかけるパパラッチ達、そして死んでいった一人の女性が姿形を変えながら絡み合っていく話だ。
立体写真を見ても立体感を感じるかどうかは人それぞれであるし、空にかかる虹を眺めてみてもそれが何色に見えるかはやはり人それぞれだろう。「平面画像を立体化する話」の話を書いてみても、それを眺めることができない人もいるし、Photoshopを使った話を書いてもPhotoshopを持っていない人には面白くないだけかもしれない、そしてオッパイ星人の話を書けば(いつもバストを大きくしがちなのは、わかりやすさの都合上だったりするだけなのだが)、それで不快になる方も多々いることだろう。
それでも、今回も立体画像の話、「平面画像立体化」の続きを書く。
さて、こんな平面画像があったとしたら、どのようにしてやれば立体化することができるだろうか?
 |
人間が立体感を感じる大きな手がかりの一つが両眼視差だ。遠くにあるものを眺める時には、右目と左目にはほぼ同じように見えるが、近くにあるものを見る時は右目と左目の場所が違うため、右目と左目では違う景色が見えることになる。例えば、下の図のように緑色の○が遠くにあって、青色の□が近くにあった場合を考えると、緑色の○は右目からも左目からも同じように見えるが、青色の□は左目からは視界の右側に見えるし、右目からは視界の左側に見える。
|
この左目と右目からの見え方の違いを頼りにして、立体感を得るのが両眼視差である。であれば、左目用と右目用に別々の画像を用意してやり、その位置のズレを意図的に作ってやれば立体的に見ることができるわけだ。
例えば、下の画像のように青色の□を右へずらしてやり、これを左目用の画像に使えば、立体感を得ることができる。
 |
下の画像はそのようにしてやることで、一番最初に示した図を立体的に見えるようにしたものである。この図は平行法= 「左目で左図を見て、右目で右図を見る」なので、遠くをぼう〜っと眺めるつもりでこの図を眺めれば、きっと青い□が近づいて見えて、この図が立体的に見えるようになるハズだ。
 |
こういった方を用いれば、立体画像を作ることができるわけで、実際「立体星座早見盤」というようなものはそういうやり方で作成されているわけではある。
だが、実は一般的に「平面画像を立体化しよう」とすると、話はそう簡単ではない。それは、こんな図を立体化しようとする場合を考えてみればわかると思う。
 |
「さっきと同じで、青い□の位置をズラしてやれば良いんじゃないの?」と簡単に言う人は少しばかり考えが足りない人である。ちょっとでも考えてみさえすれば、大きな問題に気付くハズである。この図のように背景がある場合には、青い□の位置をズラしたら、そのズレた部分は一体どうしてやれば良いのだろうか?
 |
この部分に何があるかは判らない。だとしたら、単純に青い□の位置をズラすわけにはいかない。考えてみれば、そもそも一つの目から見た情報しかないのだから当たり前なのである。もう一つの目から見た時の情報は我々の手元には無いのである。そこの部分をどうしたら良いかは我々にはわからないのである。
しかし、そうは言っても立体化するためにはこの青い□の位置を左へズラしたい。だけど、位置をズラしたらその部分が真っ白になってしまう。だけど、やっぱり立体化したいからズラしたい。"Toshift it or not to shift it; that is the question."というわけで、これはもうハムレットの心境のようになってしまう。このジレンマを解決してやらなければ、背景がある、あるいは距離の異なる物体が視野の中で重なっている平面画像を立体化することはできないのである。
そこで、「できるかな?」ではそのジレンマを解決するために、単に位置をズラすのではなくて、青い□を拡大しつつ位置をズラすというやり方を考えてみたのである。名付けて、hirax.net式「平面画像立体化法」だ。
例えば、上の画像の場合だとまずは青い□を拡大して、その後右へズラすのである。
 |
上の絵を見ればわかるだろうが、青い□を拡大してやると、元の図形と重心は同じだが、その周りに青い□が拡大することになる。そこで、その拡大した分だけであれば、位置をずらしてやっても背景の画像情報が無い場所が露出してしまう、ということがなくなる。このhirax.net式「平面画像立体化法」はつまり、隠された部分が部分的に露出してしまうのを防ぐために、それ以外の部分を隠してしまうというテクニックなのである。
そのようにして、先の一枚の平面画像を立体化すると下の図のようになる。
 |
前回作成したシャガールの「窓」hirax.net版などはそのようにして作成したものである。この画像の場合は窓枠部分は全く同じなのであるが、窓の中の景色を拡大後、左右の目用の画像をそれぞれ左右にズラしている(ズラし量は高さによって変えている。すなわち景色の中で遠くの部分と近く区の部分ではズラし量を変えている)のである。だから、よくこれらの画像を眺めてみれば、景色部分はオリジナルよりもhirax.net版は大きくなっているし、絵の中に描かれている情報自体もむしろ減少していることがわかると思う。
  |
 |
まずは、hirax.net式「平面画像立体化法」の原理がこの「画像の一部を拡大してからズラす」ということなのである。このやり方でシャガールの「窓」のような絵は立体化してやることができる。
しかし、多くの人が気付くと思うがこれだけではまだまだ不十分なのである。最初の例えのように、四角や丸の形状の物体だけがある場合などはこれで十分なのだが、一般的にはさらなる問題が発生するのである。シャガールの「窓」の場合には、窓枠がほぼ四角と丸の組合わさったような形状をしているために、その問題は発生しないのであるが、一般的な形状の場合には話はそう簡単にはいかないのである。そんな場合、すなわち四角や丸の形状の物体だけで画像が構成されていない場合には、どんな問題が発生し、それをどんな風に解決していくことができるか、については次回以降に考えてみることにしたい。
さて、冒頭で読んでいた「Right Eye」の中の「立体写真を見ることができない」という台詞はこんな感じのカメラマンに対する台詞で続けられていく。
この写真を撮った奴らは、右目(Right Eye)をなくしてる。立体感がない。正しい(=right)右目と、覗きたい左目とのバランスを失っている。物を捉える立体感をなくしたままだ。この台詞を眺めていると、前回の話を読んだ人であれば、その中で引用した南伸坊の「モンガイカンの美術館」の中で書かれている「写真の見方」の文章をきっと思い出すことだろう。
一方、カメラというのは、もともとが片目で見た映像なのである。ファインダーを覗いてないほうの目を、カメラマンがあけたままであっても、写ってきた写真は片目の映像には違いない。つまり、立体感を失った平面画像を眺めるときには、カメラマンあるいは画家と同じように覗きたい片目だけで覗かなければならないのであった。そして、その平面画像に奥行きを与えもう一度立体画像にしてやるためには、hirax.net式「平面画像立体化法」ではないが、違う場所から眺めたときに「姿を現してくる隠されたもの」についてどう対応するかということを考えてやらなければならないと思うのである。
これを両目で見れば、「写真は立体を平面に置き換えたものである」という正論が見えてしまうばかりである。だから、写真を、実物からうける視覚の印象と同じように見ようとするなら、片目で見なければいけないのである。
それは、片目で平面画像を眺めて、そして頭の中でその立体感を与える作業をしてやっても良いかもしれない。また、両目を開けて考えてみても良いかもしれない。ただ、ファインダーを覗いてないほうの目で景色を眺めようとする時には、見えていない景色を想像したり、考えたりする必要があると思うのである。その想像力は、ある意味義務でもあるし、また貴重な自由でもあるのかもしれないなと、電車の中で、ドアに寄りかかりつつ「RightEye」の最後の台詞
のこされた(=left)ものは、のこされた瞳(left eye)で、のこされた夢を見続ける義務がある、… いや自由があるを眺めながら、そんなことを考えてみたりした。
2001-02-26[n年前へ]
■過去を見る右目と、未来を見る左目と、 
Left Eye
下の写真は2週間程前に撮ったものだ。同じような二枚の写真が横に並んでいるから、容易にわかると思うが、これもある種の立体写真だ。いつもと同じように平行法で眺めてみれば、ちょっと不思議な感じの立体写真に見えると思う。
 |
これは前回の立体画像とは違って、「異なる場所から撮った二枚の画像」を眺めているわけではない。同じ場所から連写した二枚の写真を、ただ並べてみただけのものである。つまり、「異なる時間から撮った二枚の写真」を左右の目で眺めているのである。つまり、この二枚の写真は右・左の順で撮られているので、この写真を眺めるとき、私たちの右目(righteye)は過去を、そして左目(left eye)は未来を見ていることになる。
そして、街の景色は変わらないけれど、道を走る車は当然のごとく動いている。だから、車の位置は離れた時間を見ている左右の目には異なって写る。すると、私達は不思議な立体感を感じることになる。時間を立体的に左右の目で眺めることができるのである。
これまで眺めてきた立体写真は、「空間的に異なる視点から眺めた景色」を左右の目で眺めていた。そんな立体写真では、離れた場所から眺めてみても変わらずに見えるものは背景となって埋没し、離れた場所から眺めたときに姿を変えるものは背景から浮かび上がって見えた。
今回の二枚の写真は、空間的には同じ場所だけど、時間的には違う場所から眺めているのだから、やはり「異なる視点から撮った写真」に他ならない。だから、この写真を眺めるときに私達は時間を立体的に眺めていることになる。時間が経っても変わらなかったものは、背景となって埋没し、「時間と共に変わっていくもの」が背景から浮かび上がり、あるいは、背景のさらに背後に引っ込んでしまう。そんな景色を眺めるとき、私達は時が流れていくさまを両目で見ることになる。私達の過去を見る右目と、そして未来を見る左目と、私達は同じはずの場所に立っているにも関わらず、その両目から見る景色の違いに驚くのだ。
そんなことは写真だけでなくて、どんなものでも同じことだろう。例えば、言葉だってそうだ。同じようなことを書いているだけなのに、時間が流れているせいなのか、あるいは他の何かのせいなのか、言葉から受ける印象は刻々と変わっていく。同じ言葉を書いていても、読んでいても、時間が経つと共にその言葉の姿は何故か変わる。同じはずの言葉が、姿を変え、意味を変え、違う印象を与える。
上の写真の中から「変わっていったもの」が背景から浮かび上がり、私達の目の前に飛び出してきたように、言葉の場合も同じ言葉だったはずの言葉が何故か背景から浮かび上がって、私達に迫ってくることになるのかもしれない。何故だかわからないけれど、前回の最後
のこされたものは、のこされた瞳(left eye)で、のこされた夢を見続ける義務がある、… いや自由があるを読み直しながら、私はそんなことを考えてみたりした。
2001-09-25[n年前へ]
■純愛で世界を描ききれ 
Study of the Regular Division of the Plane with Innocent Love
先日、出張先で話をしようとした途端、いきなりこんなコトを言われた。
「最近、更新頻度が下がってますねぇ、あとアッチ系のネタが多いですねぇ。」また別の人には、
「たかが風圧がオッパイに思えるものでしょうか?自分には、そこがなんとも不思議で納得できないのであります。」などと言われた。本来、私は真面目な話をしに行ったハズなのであるが、思わず弁解したくなって、
「一体、指の何処でその感触を感じると思われますか?」
「それに、モンローウォークの動画はまるで全裸みたいに見えて、思わず自分はウィンドーを閉じてしまったのであります。」
「いや、掌の広げ方次第で、空気が指に与える圧力が動的に変化するのだが、その指の動きに応じて動的に弾力が変化するさまがアノ感触に近いという想像は如何なものだろうか?たかが風圧、されど風圧、と謙虚に考えるべきではないだろうか?」とか
「空気流が指の側面を押す力が主たる個所だろう、それすなわち、指の周りからこぼれるおちるアレが指に与える感覚なのである。」とか、
「実はOLスーツ編の動画も作成したのだが、そっちの方が私的にはイヤラシク倫理的にNGだったのだ。」とか色々言ってしまったのである。しかし、実はその話をしている仕事場には他にも人が何人もいて、しかもその人達には私は面識は無い。ということは、私は他人の仕事場にイキナリ来たと思ったら、「アノ感触」とか「OLスーツ」とかそんなことを話し出すトンデモない奴にしか見えないのである。これはちょっといけない。いや、かなりマズイ。
そこで、そんなことを言われないために、今回は「できるかな?」のスタート地点である「画像」の話題を考えてみたい。しかも、ただ考えるだけではつまらないので、「できるかな?」風に「愛」を込めて「画像」について考えてみたい、と思う。というわけで、今回は題して「純愛で世界を描ききれ」である。
八月に台風が関東地方を直撃した日、私は東京タワーのすぐ横で「高画質化のための画像処理技術」という研究会を聴講していた。会場に辿り付くまでの間ひどい雨と風に襲われて、最初のうちは「こ・これは、風速25m/s位はあるな。ってことは25mx 3600 s /1000mで時速90kmか…ってことは、計算によればE〜Fカップが今まさに体中にぶつかってきているのかぁ!」なんて(自分を元気づけるために)考えていたのだけれど、風だけでなくて雨もひどかったので、ついには濡れねずみになってしまい、ただ「………」と何も考えずとぼとぼ歩くだけのゾンビ状態になってしまった。
何はともあれ、そんな感じでやっとのこと会場に辿り付いて、いくつかの話を聞いていたのだけれど、その中でもとても面白かったのが、大日本印刷の阿部淑人氏の「シミュレーテッド・アニーリングによるディザマトリックスの最適化」という話だった。色々な項目を適当に重み付けしながら、ハーフトーンパターンを自動で生成して、理想のハーフトーンパターンを作成しよう、というものである。その話の後半では、工芸的なスクリーンの話も俎上に上がり、M.C.Escherの"Sky& Water I"をグラデーションの例に挙げてみたり(残念ながら実際にそんなハーフトーニングをしたわけではないが)、菩薩像を般若心経でハーフトン処理してみせたり、となかなか「できるかな?」心をくすぐるものだった。そこで、私も似たようなことにチャレンジしてみて、さらにはM.C.Escherの版画を使ったハーフトーニングを行ってみたいと思うのである。
 |
そもそも、ハーフトーニングとは多値階調を持つ画像などをニ値出力の(もしくは少ない階調しか持たない)機器で出力するために、多値の階調をニ値(もしくは少ない階調)の面積比率で置き換えることにより出力する方法のことである。例えば、下の例はグレイスケールのグラデーションパターンを円スクリーンによりハーフトーニングしたものである。
 上を円スクリーンによりハーフトーニングしたもの  |
Photoshopを使っている場合には、簡単に任意形状のハーフトーニングを行うことができる。例えば、こんなパターン![]() をカスタムパターンとして登録すると、そのパターンとの明暗比較を行うことにより、
をカスタムパターンとして登録すると、そのパターンとの明暗比較を行うことにより、
という風にニ値化ハーフトーニングを行うことができる。ところが、じゃぁこれと同じようにEscherの版画を使ってハーフトーニングしようと思っても、そう簡単にできるわけではない。なぜなら、このハーフトーニングが明暗比較によって行う以上、ハーフトーニングに使うパターンは多値の画像でなければならないのである。
Escherの版画も版画という(例えば白か黒かといった)ニ値の出力機器を用いているため、やはりニ値の画像に過ぎない。例えば、下の版画はEscherの”Studyof the Regular Division of the Plane with Horsemen”である。
 |
上の版画の一部を(ちょっとだけ細工をしつつ)抜き出してみたのが下の画像だが、白黒半分づつのニ値画像であることがわかるだろう。また、きれいな繰り返しパターンになっていて、平面にこのパターンできれいに埋め尽くすことができるのがわかるだろう。
 |
この画像をPhotoshopのカスタムパターンを用いて、グレイスケールをニ値化ハーフトーニングすると、この画像がニ値画像であるため、下のように階調をきれいに出力することができず、結局のところ「黒か白か」といった階調飛びの画像になってしまうのである。
 |  |
そこで、まずはニ値の画像を元に多値のハーフトーン用パターンを作成するプログラムを作成してみた。作成するやり方としては、初期値を元にして暗い方。明るい方それぞれの方向にローパスフィルターで演算をしつつ、256階調分のハーフトーンを作成し、さらにそれをPhotoshopで処理できるように多値画像として出力することができるようにしてみた。先の発表のやり方で言えば、「高周波を減らす」という項目に重みをおいて、ハーフトーンパターンを自動生成するアプリケーションを作成してみたわけだ(バグ満載状態で)。説明は一切無し、しかもボタンを押す順番を間違えると上手く動かないという状態ではあるが、一応ここにおいておく。名前はhiraxtone.exeでバージョンは0.0…01という感じである。(白黒ニ値だけど24bitモードの)Bitmapファイルを読み込んで、多値のスクリーンを生成するようにしてある。
それでは、このhiraxtoneを用いて、ニ値画像を元に作成した多値階調ハーフトーンパターンの一例を次に示してみる。これは、先の"Studyof the Regular Division of the Plane with Horsemen"の一部分を縮小したニ値画像をもとにして処理してみたものである。 |  |
でもって、上で作成した多値階調ハーフトーンパターンを用いて、グラデーションパターンをハーフトーニングしてみた例が下の画像である。「単純にパターンニ値化した場合」と違って、「hiraxtone1で作成したパターンを使用した場合」はグラデーションが保持されているのがわかると思う。また、階調が保持されているというだけではなくて、まるでEscherのオリジナルの"Studyof the Regular Division of the Plane with Horsemen"のようなパターンにできあがっていることも判ると思う。
 |  |  |
さて、ニ値画像パターンを利用してハーフトーニングすることができる、となると他にも色々と遊ぶことができる。例えば、自分だけのハーフトーンパターンを作ってみたくなることだろう。そして、さらにはその素晴らしいスクリーンに自分の名前を付けて広めてやりたい、と思うのは至極当然の話である。古くはBayerなどがそうしたように、自分が作ったスクリーンに自分の名前をつけてみるわけだ。
とはいえ、私が仮にスクリーンを作成してみたところで、そのスクリーンを私の名前で呼んでくれる保証はどこにもないのである。そこで、卑怯な手ではあるが、自分の名前を元画像にしてスクリーンを作成してみることにした。こうすれば、否でも応でもこのスクリーン形状を呼ぶために人は私の名前を使うことになるわけだ。
というわけで、私の名前「純」という漢字を元データにして、ハーフトーンスクリーン「純」を作成してみた。また、「純」とくれば当然もうひとつ「愛スクリーン」もさらに作ってみた。いや、別に「純愛」を目指そう、と気負っているわけではなくて、単にうちの兄弟は長男が「純」で長女が「愛」なのである。いや、少し気恥ずかしいけど、ホントの話そうなのだからしょうがない。
さて、作成した「純・愛スクリーン」さえあれば、「純愛」で世界を描ききることができるわけで、早速描いてみたのが、下の仲間由紀恵である。オマエの世界イコール仲間由紀恵か?とか、ソレってホントに「純愛」か?とか、つまらないツッコミを入れられそうな気もするが、そんなことはどうでも良いのだ。私はTRICK以来仲間由紀恵のファンになってしまったのだから、しょうがないのである。そしてまた、「純愛」を馬鹿にしてはイケナイ、と私は少しばかり思うわけなのである。(私の名前だから)
 |  |
上の二枚をじっくり眺めてみると、結構キレイに仲間由紀恵が描かれていることが判ると思う。しかも、他でもないこの二枚の画像において、私は「純愛」で仲間由紀恵を描ききっているのである。これより、「純」で「愛」な仲間由紀恵はそうそういないハズなのだ。きっと、本物の仲間由紀恵が見たら「何てピュア〜でラブリーな私かしら。きっと、これを描いた人は心のキレイな人なのね!」と感激すること間違いなし、なのだ。
ちなみに、「純愛スクリーン」でハーフトーニングした仲間由紀恵の左眼の部分を拡大してみたのが下の二枚の画像である。瞳の奥にも、「純」と「愛」が溢れていることが判るハズである。それは言い換えれば、この仲間由紀恵の瞳は「純」イコール「私」で満ち溢れ、さらにはその瞳は「愛」で満ち溢れているのである。
(目の部分の拡大図) 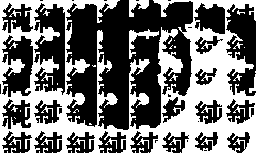 | (目の部分の拡大図)  |
う〜ん、正直ちょっとムナシイけれど、だけどちょっと気持ちが良いのもまた事実なのである。やはり、「純・愛スクリーン」で描かれる世界はとても素晴らしい世界なのである。そうなのである。
さて、今回作成したhiraxtoneは、実際のところ自分でも言うのもなんだが、本当のところ今ひとつキレイな出力ができないし、大体思ったように動いてくれないのである。低周波優先として重み付けをしたハズなのに、どうもそんな風に動いていないし、計算にも時間がかかりすぎる。全てはビールを飲みながら行き当たりばったりにプログラミングするところがいけないのかもしれないが、どうも今ひとつなのである。また、本来であればもう少し元データの形状を残すことを優先(それは高周波優先にならざるをえないだろう)にするようなオプションもつけてみたいのである。
が、とはいえ今回はいい加減思いページになってきたこともあるし、ちょっと疲れてきたこともあるし、とりあえず「純愛」で世界を描ききったところまでで今回は終りにして、続きは次回以降に遊んでみたいのである。
