2000-08-13[n年前へ]
■WEBの時間、サイトの寿命 
ゆっくり長く続けましょうか?
以前、
でロゲルギストが- 第五物理の散歩道 ロゲルギスト著 岩波新書 「通信を考える」
- その系の情報処理の単位時間
- その系の信号の伝わる速度
- その系の空間スケール
- 空間スケール < 情報処理の単位時間 × 信号の伝わる速度
- 大人数から構成される企業のスピードは、少人数から構成される企業のそれには遙かに及ばない
ところで、ロゲルギスト達はある系の「単位時間・信号伝達速度・大きさ」の間の関係について、
- 「単位時間・信号伝達速度」を入力値として、「大きさ」を考える
- 「大きさ・信号伝達速度」を入力値として、「単位時間」を考える
さて、寺田寅彦が「単位時間・信号伝達速度・大きさ」について、さらにどのようなことを展開していたかというと、それはある系の「大きさ・寿命」についての関係である。寺田寅彦は
- 空想日録 三 身長と寿命 (寺田寅彦随筆集 第四巻 岩波文庫 小宮豊隆編)
- 人体感覚について振動感覚の限界を調べた実験データ、 - 人は自らの体の固有振動周波数の振動に対してもっとも過敏である- 、というものをきっかけとして、
- 生物の時間の長さの単位は相対的なものである
- ある系の「時間の長さの感覚 = 相対的な単位」はその系の固有周期と密接な関係がある(振り子時計なんてわかりやすいだろう)
- ある系の「寿命」を測る単位は、その系の「時間の相対的な単位」、すなわち、その系の固有周期だと想像してみよう。
- その場合、ある系の固有周期はその系の大きさに比例するから、大きい動物ほどその系の「時間の相対的な単位」は長いものとなり、見かけ上の「寿命」はその動物の「大きさ」に比例するだろう。
なるほど、サイズが小さい動物(すなわち固有振動の波長の短い動物)にとっては、ほんの小さな変化も大きな変化である。ということは、その動物の感じる「時間単位」は短くなければ、生き残れないだろう。逆に、サイズの大きな動物は俊敏な動きはできないわけで、その動物の「時間単位」は長くならざるをえないだろう。
ゾウのような大きい動物は「時間単位」が長く、一見「寿命」が長いように見え、ノミのような小さな動物は「時間単位」が短く、一見「寿命」が短く見えるというわけだ。実は、ゾウもノミもその動物自身の「時間単位」を基準にすると、同じ寿命を生き抜いているということになる。
本川達雄の中公新書「ゾウの時間 ネズミの時間」では- 体重の4分の1乗に比例して「その動物の時間単位=生理的時間」が長くなる-と述べられているが、昭和八年に既に寺田寅彦は体重は身長の3乗に比例する、逆に言えば体重は身長の3分の1乗に比例するから、「体重の3分の1乗に比例して時間が長くなるだろう」と想像を巡らせているのである。素晴らしい、想像力である。
さて、寺田寅彦はロゲルギストと違って、「単位時間・大きさ」については言及しているが「信号伝達速度」については触れていない(その替わり、さらに「寿命」にまで触れているわけであるが)。もっとも、私があえて書き加えてみるならば、ある系の固有振動にはその系の中での弾性が密接に関係するし、弾性はその中での弾性波の速度も密接に関係する。つまり、ある系の固有振動の周期というものには「その系中での波の伝達速度」が暗に隠されていて、寺田寅彦は単にそれを一定とおいていたわけで、寺田寅彦が述べた内容は実はロゲルギスト達の述べた内容を包括している、と私は思うのである。
このような「単位時間・大きさ・信号伝達速度・寿命」に関する話は動物に限るものではない。
- ロゲルギストが「信号伝達速度=光速度」として、「処理速度を確保する」ための人類の行動範囲について論じたり、
- 私(いきなり自分を例に出すのも何だが)が「信号伝達速度の変化」と「大きさ(人口)の変化」から人類の処理速度の変化について論じたり
さて、前振りが長くなった。前回、
では、単に「信号伝達速度の変化」と「大きさ(人口)の変化」を並べて「処理速度」の変化について考えてみただけだった。今回は寺田寅彦が考えたのと同じく、「信号伝達速度」と「大きさ(人口)」から「寿命」が決まると考えることにより、「人類」の「寿命」の変化について考えてみることにしたいと思う まずは、前回使った「人類の大きさ=人口」の変化が次のグラフである。ただし、この人口は全然正確ではないし、むしろかなり不正確なものであることは先に断っておく。ここでは、細かな値を使うのが目的ではないので別に構わないだろう。
 |
そして、「人類」の中での「情報伝達速度」の変化を示したものが次のグラフである。この速度が「人類」という集合体の中での波の進行速度を決めるのである。
 |
それでは、「人類」という集合体の固有振動はどうやって扱うかというと、この
- 「人類の大きさ=人口」
- 「情報伝達速度」
- 人口 / 情報伝達の速度
その、人口 / 情報伝達の速度 = 「人類の固有時間」を計算してみたものを次に示してみよう。
 |
こうしてみると、人類というヒトの集合体においては、どんどん時間の流れは速くなり、それに応じて見かけの「寿命」は短くなっている、ということがわかる。人類はまさに生き急いでいるのである。もし、この流れを止めようと思ったら、どうしたら良いだろうか?それには、今回の計算から言えば情報転送速度を遅くするか、人類の大きさを大きくするしかない。情報転送速度を遅くするのはなんとも後ろ向き(byわきめも)だし、人口を減らすというのもなんとも後ろ向きだ。だとしたら、宇宙へでも人類が進出して、人類の空間的なスケールを大きくしていくしかないのだろうか?これもまた難しい話である。
さて、最近、大好きなWEBサイトが閉鎖してしまったり、更新速度が遅くなっていたりしていて少しさみしい。だけど、もしかしたら各WEBサイトにも、「更新速度が速いと、WEBサイトの寿命が短い」なんて法則が実はあるのかもしれない。更新速度が速いということは、そのWEBサイトの固有時間が速く流れているということで、限られた寿命をどんどん使い果たしているのかもしれない。
だとしたら、更新速度が遅いということはそのWEBサイトの寿命が長くなるということだから、それはそれで良いのかなぁ、などと思ってみたりする。「太くて短い寿命」も「細くて長い寿命」も実は本人からすればどちらも同じ長さなのかもしれないけれど、外から見ている私は「細くても良いから長く続いて欲しいなぁ」なんて思ってもみたりするのである。
2002-04-24[n年前へ]
■視線のベクトルは未来に向くの? 
マンガのストーリーの方向を顔向きで探る 前編
一年くらい前から、コンビニで300円ほどの安いコミックをたまに買うようになった。休日の早朝、コンビニで発泡酒とおつまみを買って、ついでにそんな安いコミックを買って、そして、ビールを飲みながらそれを読むのがワタシの休日のささやかな(だけど至高の)幸せなのである。そんな至高の幸せをかみしめるとある休日、286円の西岸良平の「三丁目の夕日」を読みながら、ワタシはふと思ったのである。
これまで、「できるかな?」では、様々な小説、例えば「星の王子さま」「明暗」「こころ」「草枕」「失楽園殺人事件」といった小説を色々と解析してきた。そして、その中の主人公達がどんな風に動いていくのかとか、作者が何を考えているかとか、あるいは、犯人は誰かであるのか、などを調べてきた。何でそんなことを考えるの、と人には聞かれそうだけれども、とにもかくにもワタシはそんなことを考えてきたのである。そして、さらにふと考えてみれば、ワタシの至高の幸せを支える素晴らしき286円のマンガ本に関して、ワタシはストーリー構造などを真剣に考えてみたり、調べてみたりしたことはなかったのである。イケナイ、イケナイ、こんなことでは「恩知らず」野郎としてワタシにはバチが当たってしまうに違いないのである。
そこで、今回「コミックの中のストーリー構造」について調べてみたい、と思う。コミックの中で主人公達がどのような方向へ進もうとしているのか、あるいはその歩みの中で主人公達は一体何を考えているのか、などについて少し調べてみることにしたのである。
これまで、小説中のストーリー構造や主人公達の動く方向を調べるときには、「特定の言葉や主人公達」が登場する位置を調べたり、あるいは他の言葉や登場人物との相関を調べたりしてきた。それでは、一体マンガのストーリー構造や主人公達の動く方向を調べるにはどうしたら良いだろうか?そんなものどうやって調べるの?と一瞬悩んでしまいそうではあるが、ちょっと考えてみればそれはとても簡単なのである。小説と違って、マンガでは登場人物達がちゃんと見えるカタチで描かれているのである。主人公達がどの方向を向いているかがちゃんと描かれているのである。そしてまた、主人公やその周りの人々や、ありとあらゆる人々がどんな方向を向いているかがもうありのままにちゃんと描かれているのである。
だったら話は実に簡単、マンガの中の登場人物達の向きを刻々調べてみれば、そのマンガのストーリーの中で主人公達がどちらへ向かって何を見ながら動いているかが判る、というわけだ。実に即物的でシンプルなアプローチである。
善は急げ、というわけで、早速今さっきまで読んでいた手元に掴んだままの西岸良平の「三丁目の夕日 ジングルベル」の中から、「霜ばしら」という短編を題材にして、その中の主人公の顔の向きを調べてみることにした。ある恋人同士の、とても楽しくて、そしてとても悲しい物語である。
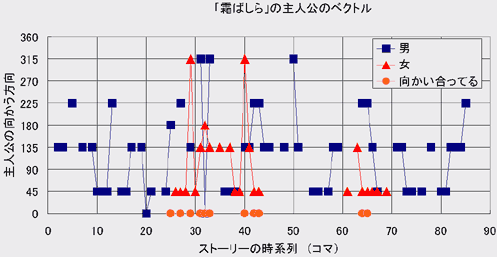
まずは、マンガのコマ中の登場人物達の向きと角度の対応表を下の表のように定めた。登場人物がコマ中で右方向を向いているときに0度とし、正面方向(すわなち読者方向)を向いている時が90度。コマの左方向を向いていれば180度である。そして、280度では真後ろを向いているという具合である。
270 | ||
180 | 0 | |
90 |
このようにコマの中に登場する主人公達の向きを数値化することにして、話の冒頭から結末までの各コマ中での主人公(周平)とその恋人(アキちゃん)の向きを調べてみたのが下のグラフである。青色の四角が主人公で、赤色の三角がヒロインである。また、その二人が向かい合ってる場合には朱色の丸を方向=0の位置に書き入れてみた。グラフ中では水平軸がストーリーの時系列で、左端が話の冒頭であり、右端が話の結末、そして縦軸が「主人公達の向かう方向」である。また、ヒロインのアキちゃんが途中の2カ所にしか現れないのは少しばかり悲しいストーリーのせいだ。この「霜ばしら」は主人公とアキちゃんの涙を誘う悲しい物語なのである。
左端 = 話の冒頭 右端 = 話の結末 縦軸 = 主人公達の向かう方向
|
このグラフを少し眺めていると大体の特徴が見えてくるだろう。すなわち、
- 主人公達はほとんど45、135、235度の3方向しか向いていない
- それ以外の向き(例えば315度)を向く場合などは、ほとんどが「向き合っている」場合である
- そして、135度の方向を向いていることが圧倒的に多い。
しかし考えてみれば、これらの特徴はごく当たり前なのである。まずは、舞台やテレビと同じく、登場人物達は読者にお尻を向けるわけにはそうそういかない。読者に顔を見せずにお尻を向けていたら、誰が誰だかよく判らなくなってしまうに違いない。だから、登場人物達はあまり後ろを向くわけにはいかない。どうしても、主人公達は文字通り「前向き」にならざるをえない。もし、後ろを向くとしたら、それは文字通り登場人物達に「後ろを向かせる」何らかの強い意図に基づく場合以外ありえないに違いない。それが、例えば他の誰かと「向き合って」いる場合であったり、あるいは他の表現意図に基づくものであろう。
また、日本におけるマンガが右から左に読まれていくのであるから、読者の視線の動きの中では「右のコマ= 過去」「左のコマ = 未来」と時間感覚が成立している。マンガを読む私たちの視線のベクトルは右から左、過去から未来へと進んでいるのである。すなわち、「マンガの中の話の流れ= マンガの中の時間・因果の流れ」をスムーズにするためには、主人公達が過去なり未来なりのコマの方向を向くことで、時間の流れ=因果の流れをスムーズに受け継ぐのが自然だと考えられる。過去に発生した「何か」に応えた反応をするならば、主人公達は当然右を向くし、そうでないならば通常は時間の流れる先の向き= 左側を向くことになるだろう。
すると、マンガの中の登場人物達は読者に対して「前向き」であって、なおかつ時間の流れる方向に前向きの「左側」を向くのがごく自然である、ということになって、「コマの中の主人公達は135度の方向を向くことが圧倒的に多い」ということになるのだろう。まぁ、当たり前の話である。
そしてさらには、こんな風にも考えられる。「右<->左」方向は時間の流れに対する主人公達の向きであって、「前向き<->後ろ向き」は登場人物達が文字通り「前向きであるか」あるいは、あるいは「後ろ向きであるか」という「主人公達の内たる気持ちの向き」ではないだろうか、とも考えられるのである。
だから、例えばこの「霜ばしら」の結末の部分80コマ以降を見ると、45->135->225度という主人公のベクトルの変化がある。これは主人公が「過去に向かう向き(死んでしまったヒロインへを見る向き)→未来に向かう方向へ進む→未来に向かう(だけど、やはり亡くなってしまったヒロインをたまに振り返りながら)」というまさに主人公のベクトルを描き出しているのではないだろうか、と思うのである。そんな風に眺めてみれば、最後のコマの主人公の向きが「何かを振り返りながら、だけど未来へと歩いていく様子」をまさに映し出しているようにも見えるのである。ストーリーはここに書くわけにはいかないけれど、こんな想像も割と良い線をいってるのかもしれない、と思ってみたりするのだ。
 |
こんな風に、単にマンガの登場人物の向きだけで主人公達の向かうベクトルを探る、なんていうことが乱暴なのはさらさら承知の上である。こんな人物の配置解析によるストーリー解析が的を射ているのか、あるいは的を外しまくっているのかは、ぜひこのマンガを読んで実際に判断してみてもらいたい、と思うのである。
さて、こんな風に舞台の右と左、上手と下手に対してどんな風に登場人物達が向かっていくのか、なんてことを考えるといろんな想像が広がってとても面白いのである。時間の進むベクトルであるLeftStage(舞台から見ると逆なんてことは言わずに)に消えていく登場人物達(例えば今回の話では恋人アキちゃんを亡くしてしまった主人公)は「残されたもの達」を連想させてみたり、あるいは、色んなものを眺める私たちの視線のベクトルは本当に未来に向いているのかな?などと色んな想像や空想を駆けめぐらせてみることも、それはそれでとても趣深いことだなぁと思うのである。
2003-07-12[n年前へ]
■14ミリグラムの「いろんな気持ち」 
気持ちを軽くする「息抜き」化学式
小学校の頃、ダンボールのような不思議なものをかぶる人を描いた挿絵とともにこんな話を国語の教科書で読んだ記憶がある。この記憶の隅に残り続けている話は、乙骨淑子の「すなの中に消えたタンネさん」という物語らしい。この物語のように、悩み事を砂に変えて消し去ってくれるなんて機械がもしもあったとしたら、私だって欲しくなってきっと一つ注文してしまうかもしれない。そして、結局は「空色のせんたく機」のバックオーダーをさらに一つ増やしてしまい、タンネさんをさらに追いつめてしまうことだろう。
発明家タンネさんが作り出した「悩み事を砂に変えてしまう洗濯機」のような、いろんな気持ちを何かの物質に変えてしまうような「気持ち・物質」交換機なんていうものがあるという話は残念ながらまだ聞いたことがない。だけど、もしも、そんなものがこの世の中にあったとしたらそれは一体どんなものなのだろうか?
それは一体どんなものだろう?と想像してみようと言ってみても、いろんな気持ちを何かの物質に変わるだなんて、何をいきなり荒唐無稽なことを言うのだろうと思われるに違いない。けれど、少し振り返って考えてみたりすれば、悲しい気持ちがいつのまにか涙に変わったりする、なんてことであればそれはとてもよくある話だと思う。そんなふうに、「悲しい気持ちが涙という水に変わったりするなんて」ことが当たり前のようにあるとするならば、「いろんな気持ちが何かの水に姿を変えて、そして気持ちが水とともに消え去っていく」ことが当たり前のようにあったとしても、それは別に不思議な話でもないようにも思われる。
例えば、人が息を吸いこむと、一呼吸あたり約17ミリリットルの酸素が体の中に取り込まれる。そして、その酸素は体の中で糖分と反応して二酸化炭素と水に変わる。化学式で書いてみれば、C6H12O6+6O2+6H2O→6CO2+12H2Oという反応が起こるわけだから、一回分の呼吸から14ミリグラムの新たな水が体の中で作り出されるわけだ。いろんな気持ちが「涙という水」に姿を変えることがしばしばあるように、この呼吸の中で作り出される「14ミリグラムの新たな水」が実は体の中の「いろんな気持ち」が姿を変えたものだと考えてみるのも少し面白いと思う。呼吸の結果起こるC6H12O6+6O2+6H2O→6CO2+12H2Oという化学反応が実は「気持ち・物質」交換を示す化学式だったと考えてみると、少し面白いことを思いつく。
例えば、こんな風に考えてみよう。体の中に悲しい気持ちを抱えたまま、息を吸ってそしてため息をつく。すると、その悲しい気持ちが体の中で14ミリグラムの水に姿を変える。そして水に姿を変えた14ミリグラムの悲しい気持ちはいつの間にか体の外に排出されて消えていく、と考えてみる。一回呼吸をすれば、一回ため息をつけば、14ミリグラムの悲しい気持ちが体の中から消えていく、と考えてみるのである。一回の呼吸で14ミリグラムだけ気持ちが軽くなる、と考えてみる。体や心を休めることを「息抜き」と表現するけれど、それは息をするおかげで気持ちが軽くなるこの「気持ち・物質」交換を示す化学式に基づいていたのだ、と空想してみるのだって面白いに違いない。C6H12O6+6O2+6H2O→6CO2+12H2Oという化学式に「息抜き」という言葉が基づいていた、と考えてみるのである。
あるいは、こんな風にも考えてみる。一回の呼吸で14ミリグラムの色んな気持ちが14ミリグラムの水に姿を変えるのでれば、それは一生を通して考えてみると
残念ながら、タンネさんの「空色の洗濯機」はまだ世の中にはない。だけど、こんな風に呼吸が実は「気持ち・物質」交換機かもしれない、と考えてみると少しは息抜きになりそうなことを思いつく。例えば、いつもより色んな気持ちを抱えているときには、いつもより大きく息を吸って、そしていつもより大きく息を吐いてみる。そうすれば、きっといつもより多くの「いろんな気持ち」が水に変わる。いつもより多く、もしかしたらそれは数ミリグラムだけしか多くないかもしれないけれど、いつもより気持ちがほんの少し軽くなるかもしれない。
■14ミリグラムの「いろんな気持ち」 
あるいは-気持ちを軽くする「息抜き」化学式-です。気持ちが落ち込むときには、ため息をつくか、あるいは深呼吸をするしかないかな、というような「息抜き」空想話です。ロボットじゃない人間は呼吸をするしかないのかな、と。
2004-06-14[n年前へ]
■「電車で座る女性のパンツが見える範囲」について 
空想科学大戦2http://www.amazon.co.jp/exec/obidos/ASIN/4889919538/同・文庫版http://www.amazon.co.jp/exec/obidos/ASIN/4840108994/の、韓国版のようです。という情報を頂きました。ありがとうございます。