1999-06-10[n年前へ]
■コピー機と微分演算子 
電子写真プロセスを分数階微分で解いてみよう
前回、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
の中で、電子写真プロセスは「画像のエッジ部分が黒くなり、そうでないソリッド部分は画像が飛びやすい... 画像のエッジ部分、すなわち、電位変化が大きく、電界強度の高い部分に対してトナーが現像されやすい... 」という文章がある。この脈絡は何か見覚えがないだろうか?そう、
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の中の、「人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。」という文脈と似ている。また、「ゼロックス...」の回での(昔の)電子写真の特徴、
- エッジ強調される。
- 細かいところはボケてしまう。
参考までに、以前の話のときに用いた画像を示しておく。
まずは、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
における(昔の)モノクロコピーを模したものである。
 |  |
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の際に解析した元画像と0.75階画像である。ただし、この解析は2次元解析ではなく、1次元における計算を回転させて、中心対称な画像を作成している。その理由は前回述べたので今回は述べない。
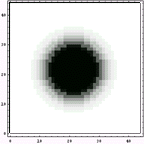 | 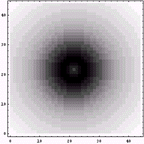 |
それでは、解析を始める。まずは、Photoshop5による「(昔の)コピー機シミュレーション」である
 |  |
次が、分数階微分画像だ。今回もMathematicaを用いて計算している。検算が終了したら、Notebookも公開予定だ(実は検算が終了していないのだ...)。
 | 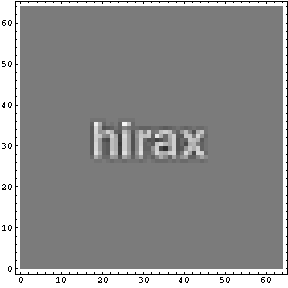 |
胸を張って「似ている」と断言するつもりはないが、少しは似ているのではないだろうか。別に似るまでがんばっても良いのだが、この分野の話はあまりやりすぎるわけにはいかないのである。ということで、強引ではあるが、今回の話の結論は「アナログコピーはオリジナルコピーの0.75階微分だ」というところで終わらせてもらう。
今回は、コピー機によるコピーを微分演算子と結びつけてみたわけだが、複数回のコピーに適用してみると面白いだろう。例えば、孫コピーは0.75+0.75階微分=1.5階微分であるとかだ。
また、同じ現像プロセスといっても色々あるわけであるから、各現像方式により微分演算子の階は異なるのが適当だろう。例えば、この機械は0.8階微分(つまりほとんどエッジ現像)であるが、こちらの機種は0.05階微分(極めて元画像に近い)で再現性に優れる、などという論議もできるかもしれない。
ところで、某所で今回の話と似て非なる話がCoffeeBreakとして公開されている。しかし、そちらは一般公開されていない。というわけで、今回は分数階微分の第3話ではなく、第4話ということになる。STARWARS風に言えば、Episode4だ。STAR WARSのようなSF映画もそうであるが、こういった話は生物(なまもの)である。ずっと置いておくと腐ってしまう。「腐ってこそ美味い食べ物もある」、という反論も聞こえてきそうだが、そういったものは少数の例外である。味オンチの料理人の作ったものではあるが、どうか賞味期間内に味わって頂きたい。
1999-07-05[n年前へ]
■目に映る明るさって何ですか? 
君は天然色
前回、デジカメ画像をスクリーンセーバーにしたい-記念写真を飾ろう - (1999.06.30)
を作るために、いくつか調べ事をした(ホントはずっと昔に)。それについてまとめておきたい。
調べたことは、
- カラーから白黒への変換はどうする?
- セピアカラーって一体何だ。
- セピアカラーへの変換はどうやろう?
カラーから白黒への変換はどうする? どうしよう? これは結構難しい問題(結果的にやったことは簡単でも、プロセスとしてはすごく難しい)だ。そうそう白黒の世界を見たことのある人はいないだろう。特殊な状況下(たとえば、すごく暗い所とか)では色を感じないこともあるだろうが、普通の世界は天然色である。フルカラーの世界だ。そもそも明るさって一体何だ?(明快に答えられる方教えてください。) 例えば、下の図で明るい順番はどうなっているだろうか?自信を持って答えられるだろうか。
 |
とグチを言っていてもしょうがないから、決めてしまおう。うす暗い(1lx程度)部屋で景色を眺めてみよう。その時見える世界が、明るさの世界だ。そこには色など存在しない。確かめて欲しい。今回は、とにかくそれを「明るさ」の尺度としてしまおう。
(興味ある方は明るさを測ろう- 新技術の女神 -(1998.11.13)もご覧下さい)
次に明るい部屋へ移動する。そこでは、新たなものが加わる。それが「色」である。ということで、「明るさ」+「色」で世界を表現することにしよう。
いきなりではあるが、人間が光を感じる網膜内の光受容器には錐体と桿体がある。
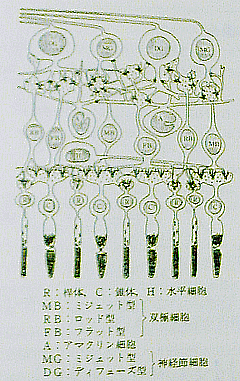 「視覚と画像」 大頭・行田 著 森北出版より |
それでは、明るい部屋で感じる色はどうなっているだろうか。色を感じる錐体の中には波長感度の異なる3種類の視物質がある。それぞれの波長感度を以下に示す。
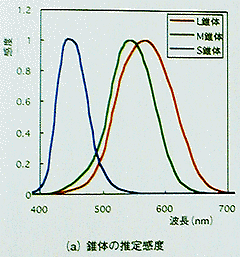 CQ出版 洪 博哲著 「お話・カラー画像処理」より |
次に、それらの3種類の視物質による錐体が組み合わさった時の波長比視感度を以下に示す。点線で示してあるほうは比較的暗い場所での波長比視感度なので、今回は無視して欲しい。
 「視覚と画像」 大頭・行田 著 森北出版より |
後は、このグラフを元に赤、緑、青の3点で重み付けしてやれば良いだろう。
というわけで、グレー化のために使っているのはこの式だ。
- Red: ptr[2]
- Green: ptr[1]
- Blue: ptr[0]、として
やっと、ここまで辿りついた。結局使うのはこんな簡単な式なんだ、っていうツッコミは無しにして欲しい。同じ式を使うのでも、私はそこまでのプロセスも重視したいのだ。
さて、こういった色を扱う話題であれば、脇色彩研究所のWEB(http://www.mmjp.or.jp/rwicp/ )中から
- 色に対する感じ方(眼とフィルム)( http://www.mmjp.or.jp/rwicp/data106.html )
- カラーフィルムの特性と色再現( http://www.mmjp.or.jp/rwicp/filmirosai.html )
- 明るさの見え方(明暗対比)( http://www.mmjp.or.jp/rwicp/data506.html )
- 色覚、眼の色に対する感じ方( http://www.mmjp.or.jp/rwicp/data509.html )
また、文中でも書いたが、「明るさとは***ということだ」と明快に答えられる方は私に是非教えて頂きたい。もし、素晴らしい答えが頂けたら、粗品(言葉通りの)を進呈しても良いと思っているくらいだ。
なお、以下のような答え方は遠慮致したい。
例1:
私 「液体と固体はどう区別するの」
A 「融点を境にして上と下」
私 「....」
例2:
私 「クジラは哺乳類、魚類どっち?」
A 「卵生まないから哺乳類」
私 「...」
1999-07-18[n年前へ]
■hixの地図 
好きな話は何処にある?
最近、本WEBのTopページが非常に読みにくくなっている。話題が多すぎるのだ。これでは、このWEBを見に来てくれた人がいたとしても、迷ってしまうだろう。きっと、好みに合うページを見つける前に他のWEBサイトにとんでしまうに違いない。自分の好きにやっているサイトとは言え、それは少し寂しい。そこで、自らhiraxサイトの内容について解説してみることにした。といっても、単に解説するのではつまらないので、多少の考察を含めながら、である。
他の人のWEBなどを眺めながら、自分のWEBの特徴を振り返ってみると、下のような図を持ち出すのが一番良いような気がする。これは横軸を「技術度」、縦軸を「感性度(完成度にあらず)」にしたものである。ジャンル1,2,3,4は大雑把に傾向で分類しようとしたものである。
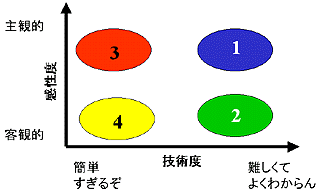 |
他の技術系サイトを見た後に本WEBを見ると、どうも本WEBは技術的でない話が多い。主観的な部分がかなり含まれているのだ。他の技術サイトでももちろん主観的な部分はある。しかも、(私にはまだまだ出来ないのだが)説得力があるのだ。すなわち、ある程度の客観性が感じられる。しかし、私のサイトの中にある主観的な話は他の人に説得力があるとは思えないのである。妙な感覚的な話と技術的な話のカクテルみたいなのである。そこで、上のようなグラフが登場するわけである。
科学という立場から考えれば、客観的であり技術的にも高度な「ジャンル-2」が望ましいだろう。しかし、本WEBには技術的には高度でないし、客観性もない、という「ジャンル-3」も多い。例えば、
iMacはドラえもんの夢を見るか? -さようなら、ドラえもん - (1999.02.03)
などがそうだ。そして、その極限として「Scraps」がある。こういった状況が良いのか悪いのかよくわからないが、とりあず、それもまた個性ということにしておこう。
「ジャンル-4」の代表的な話としては
鴨川カップルの謎 -そうだ、京都、行こう-(1998.11.29)
というところか。「ジャンル-1」としては
コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
というところで、「ジャンル-2」は
夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
という感じだろう。まずは、自分の好みとあった所から眺めてみて頂きたい。また、裏で繋がっている話も多いのでそういう伏線を探してみるのも面白いのではないだろうか。
なお、私の書く文章ははどうも「本当に言いたいことを行間に隠してしまう」ようなので(表現力がないとも言う)、行間に隠れている(作者も気づいていない)応用など読みとって頂けたら幸いである。それを私に教えていただければ、なお良い。
1999-07-25[n年前へ]
■君はトナーを見たか? 
6umの高速飛行物体
今回の話はミステリー小説のように、「嘘を意識して書きはしないが、本当のことも意識的に書かない」部分がある。お読みの際は注意が必要である。
先日、大手町で開催されていた「JapanHardCopy'99」を見ていた。ちなみに「JapanHardCopy」というのは電子写真装置(複写機やレーザービームプリンター)やインクジェットプリンターなど画像を印字する機械に関する学会である「日本画像学会」が主催するシンポジウムである。その中でも、一番よく「覚えている」発表を考察を含めながら紹介したいと思う。とても「できるかな?」と共通の匂いがするのだ? それに15分の発表がまるまるビデオ(を液晶プロジェクターに表示したもの)によるものというのも珍しいと思う(画面上に時々タイミングを知らせるマーキングが出てはいたが、発表者は喋る長さ調整に苦労していたと思う)。
それは、
現像プロセスにおけるトナー粒子の挙動測定
という発表だ。
この発表は電子写真式の装置の現像装置でトナーが現像される様子を計測した結果の報告である。以前、
ゼロックス写真とセンチメンタルな写真 -コピー機による画像表現について考える - (99.06.06)
の時に電子写真プロセスについて紹介した。今回もその簡単な構成を示しておく。このような機構がコピー機やLBPの内部には入っているのだ。(ドラム表面の画としてはRicohのWEBがわかりやすい。)
 |
上の概略図で現像装置は右の薄紫の円である。感光ドラムが中央の大きな円だ。この発表は、現像装置と感光ドラムの近接部(画面中央のの赤丸で囲まれた部分)で何が起きているかを測定しているのだ。
しかし、全ての現像装置ではなく現像装置と感光ドラムが非接触のタイプのものに関する報告である。現像装置から感光ドラムへトナーを現像させてやるわけだが、両者が非接触であるということはトナー粒子を現像装置から飛ばしてやることにより現像させるわけである。高電界を印加して電気的な力によりトナー粒子を飛翔させるのだ。そのような場合にトナー粒子がどのような挙動を示しているかを計測しているのである。
現像装置と感光ドラムの間の距離というのは通常300um程度である。また、最近のトナーの粒径は6um程度である。300umのギャップ中を6um程度の飛行物体が数多く飛びまくるのである。数多くといってもピンとこないかもしれないので、数値的な考察をしてみる。1cm^2(1平方センチメートル)の黒い四角を印刷するのにトナー粒子はどのていど必要だろうか。もしトナー1個が10um角の領域を完全に覆えるならトナーが1000x1000個あれば1cm^2の区画を完全に覆えるだろう。しかし、現実問題として1層だけでは覆えるわけがないので仮に5層必要だとすると、5x10^6個のトナーが1cm^2(1平方センチメートル)の黒い四角を印刷するのに使われていることになる。500万個である。
その数多いトナー粒子が飛行しているものの中から1個単位のトナー粒子を計測しどのような飛行をしているかを調べているのだ。数100um角の領域中で数百万個のトナーが飛行する中から1個のトナー粒子を調べるのである。まるで、大都会で一人の人の追跡取材し、その人にライトをあてるような作業ではないか。ロマンチックとは思えないだろうか?
それでは、どのように飛行しているかを予稿集の図から抜き出してみよう。
 |
この写真中では画面上のドラムと現像装置は500um離れている。また、上と下の写真ではトナーを飛行させるための電界の波形が異なる。上が単純な矩形波であり、下が矩形波の正と負の電界がかかる時間長さが異なるものである。まるでトナー粒子の動きが物理的なオシロスコープのようである。
これはほぼ1/15秒間の軌跡であり、予稿集の写真から推定するに、その間に7cm程度は移動している。ということはトナー粒子は1秒間に1m程度は移動していることになる。秒速1mである。しかも方向を鋭く変えながらであるから、加速度としては凄いものがあるし、瞬間の最大速度もはるかにこれより速いだろう。
普段LBPなどで出力をすることも多いと思うが、その出力画像を形成しているトナー粒子たちがこんなに高速でアクロバット飛行してきたとは知らなかった人も多いだろう。この写真自体は今回の発表の導入部分に過ぎなく、本題がこの後に続くのだが、結構面白い写真ではないだろうか。トナー粒子の動きが一目瞭然である。
ところで、ここまできても「おまえの考察が少なすぎるぞ。」と言われる方はいらっしゃらないですよね。「これ、おまえの発表じゃないか。自作自演じゃないか。」とおっしゃる方はいるでしょうけど。
1999-09-01[n年前へ]
■画像に関する場の理論 
ポイントは画像形成の物理性だ!?
今回は、
夏目漱石は温泉がお好き? - 文章構造を可視化するソフトをつくる- (1999.07.14)
の回と同じく、「可視化情報シンポジウム'99」から話は始まる。まずは、「可視化情報シンポジウム'99」の中の
ウェーブレット変換法と微積分方程式によるカラー画像の圧縮および再現性について
という予稿の冒頭部分を抜き出してみる。「コンピュータグラフィックスを構成する画素データをスカラーポテンシャルあるいはベクトルポテンシャルの1成分とみなし、ベクトルの概念を導入することで古典物理学の集大成である場の理論が適用可能であることを提案している」というフレーズがある。
着目点は面白いし、この文章自体もファンタジーで私のツボに近い。しかしながら、肝心の内容が私の趣向とは少し違った。何しろ「以上により本研究では、古典物理学の場の理論で用いられるラプラシアン演算を用いることで、画像のエッジ抽出が行えることがわかった。」というようなフレーズが出てくるのである。うーん。
私と同様の印象を受けた人も他にいたようで(当然いると思うが)、「エッジ強調・抽出のために画像のラプラシアンをとるのはごく普通に行われていることだと思うのですが、何か新しい事項などあるのでしょうか?」という質問をしていた人もいた。
また、話の後半では、画像圧縮のために、ラプラシアンをかけたデータに積分方程式や有限要素法などを用いて解くことにより、画像圧縮復元をしようと試みていたが、これも精度、圧縮率、計算コストを考えるといま一つであると思う(私としては)。
画像とポテンシャルを結びつけて考えることは多い。例えば、「できるかな?」の中からでも抜き出してみると、
- 分数階微分に基づく画像特性を考えてみたい- 同じ年齢でも大違い - (1999.02.28)
- ゼロックス写真とセンチメンタルな写真 - コピー機による画像表現について考える- (99.06.06)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
現実問題として、実世界において画像形成をを行うには物理学的な現象を介して行う以外にはありえない。「いや、そんなことはない。心理学的に、誰かがオレの脳みそに画像を飛ばしてくる。」というブラックなことを仰る方もいるだろうが、それはちょっと別にしておきたい。
「できるかな?」に登場している画像を形成装置には、
コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
で扱ったコピー機などの電子写真装置や、
宇宙人はどこにいる? - 画像復元を勉強してみたいその1-(1999.01.10)
で扱ったカメラ。望遠鏡などの光学系や、
ヒトは電磁波の振動方向を見ることができるか?- はい。ハイディンガーのブラシをご覧下さい - (1999.02.26)
で扱った液晶ディスプレイなどがある。そのいずれもが、純物理学的な現象を用いた画像形成の装置である。
例えば、プラズマディスプレイなどはプラズマアドレス部分に放電を生じさせて、電荷を液晶背面に付着させて、その電荷により発生する電界によって液晶の配向方向を変化させて、透過率を変化させることにより、画像を形成するのである。
 |
また、逆問題のようであるが電界・電荷分布測定などを目的として液晶のボッケルス効果を用いることも多い。液晶を用いて得られる画像から、電界分布や電荷分布を計測するわけである。これなども画像と場の理論が直に結びついている一例である。
参考に、SHARPのプラズマアドレスディスプレイを示しておく。
 |
また、電子写真装置などは感光体表面に電荷分布を形成し、その電位像をトナーという電荷粒子で可視化するのであるから、電磁場を用いて画像形成をしているわけである。だから、場の理論を持ちこむのは至極当然であり、有用性も非常に高いだろう。そういった視点で考察してみたのが、
である。 同様に、画像圧縮に関しても、画像形成の物理性に着目することで実現できる場合も多いと思うのであるが、それは次回にしておく。