1999-12-16[n年前へ]
■スキー場の特殊相対性理論 
ジャンプの飛距離は何メートルだ?
突然ではあるが、HIRAX.NETのドメインレコードを調べてみると、
Record created on 16-Dec-1998.となっている。自分のドメインのレコードをわざわざ調べたのは、一体いつ取得したのか私自身が忘れてしまったからである。何しろ、「できるかな?」は当初異なる場所での二本立てで公開していたため、私の記憶がごっちゃになっているのである。あと各回の公開順序も実はかなりシャッフルされている。そのため、完全に忘れていたのである。
「できるかな?」はHIRAX.NETのコンテンツの一部である。しかし、HIRAX.NETの誕生日よりも、「できるかな?」の誕生日の方が実は早い。
で書いたように、「できるかな?」はすでに満一年を迎えていたわけである。そしてやっと、本日でHIRAX.NETも満一歳になったわけだ。何はともあれ、目出度いことである。子供の頃やらされた「ドリル」でも3日も続かなかったのに、1年続くとは、正に奇跡である。奇跡はそうそう続かないような気もするが... さて、関係ない話はここまでである。今回の舞台は万座温泉だ。なぜなら、先週末私は万座温泉でスキーをしていたからだ。何故だか理不尽な話しではあるが、私は万座温泉でローレンツ収縮を考える羽目になったのだ。もう少し正確に言えば、スキー場で特殊相対性理論を考える羽目になったのである。(先に断っておくが、私はトンデモ話をマジメな顔で言うことが多い。)
 |
話の発端はスキーに行く前に遡る。職場の今年の新入社員であるタカノリ君(仮名)とスキーの話をしていた。彼は秋田出身であり、子供の頃からスキー三昧の生活をしていた。大学に入り京都へ行ってからは、スキーをやる頻度は下がったが、チョコチョコ行ってはいたという。
そのタカノリ君(仮名)と話していると、彼はさりげなくこう言った。
「10m位のジャンプはよくするスよ。」10mである。2mの身長の人の5人分である。それは、スゴイ。
「えぇ、本当かぁ〜〜」
「いやぁ、そんなのよくやることじゃないスか?」
今回のスキー&温泉旅行は職場(と何故か競合他社)の人達30人程で行った。ほとんどの人は、割にスキーは好きな人が多い。従って、スキーも上手い人が多い。その人達に囲まれながら、タカノリ君(仮名)は断言した。
「6,7mは簡単だけど、10mってスゴイなぁ。」タカノリ君(仮名)、ただ者ではない。
「本当かぁ〜〜」
「えっ、だってただ飛ぶだけじゃないっスか。」
そこで、スキー場でその確認をしたわけである。場所は万座プリンスゲレンデの下部である。リフトとコースが交差する辺りに、ジャンプできる場所があったのだ。そこで、彼は軽く滑り出し、力一杯ジャンプした。
果たして、タカノリ君(仮名)は何メーター飛んだのであろうか? それとも、ただのホラ吹き男爵であったのだろうか?
ところが、その答えをすぐに書くわけにはいかないのである。なぜなら、タカノリ君(仮名)がジャンプをしてみせた時に事件は起こったのである。
「どうスか!10mはいったんじゃないスか!」
「3,4mしかいってねーぞ!おイ!」
これは、一体どうしたことだろうか? しかも、会話はまだ続くのである。
「何でっスか!軽く1秒は宙に浮いてたっスよ!」ますます不思議なことに、時間感覚すら違っているのである。一体何が起こっているのだろうか?
「そんなことはねぇぞ!コンマ数秒だろう!」
私はここで気づいたのである。観測者の間で時間と空間の不一致が生じているのであれば、ここはもちろんアレの登場である。アレと言えば言うまでもない、もちろん特殊相対性理論である。
そう、万座温泉スキー場ではローレンツ収縮を実感することができるのである。「スキー場でジャンプする」という現象を考える際には、「スキー場におけるhiraxの特殊相対性理論」を導入しなければならないのであった。
それでは、簡単に「スキー場におけるhiraxの特殊相対性理論」を説明しよう。今回、生じている不思議な現象は以下のようになる。
登場人物
- タカノリ君(仮名) 速度vでジャンプをしている。
- 観客 静止している。
| タカノリ君(仮名) | 観客 | |
| 飛んだ距離 | 10 | 3 |
| 飛んでた時間 | 1 | 0.3 |
つまり、速度vで飛んでいるタカノリ君(仮名)の感じる空間や時間といったものは、静止している観客に比べて、いずれも3倍程度に膨張しているのである。
通常の世界で生じるローレンツ収縮は、速度vで移動している観測者の空間軸も時間軸も
![]()
倍縮むのであるが(ここでは光速c=1の単位系を使用している)、
であるが、「スキー場におけるhiraxの特殊相対性理論」では、速度vで移動している観測者の空間軸も時間軸も静止している観測者に対して、逆に![]()
倍に延びてしまうのである。もし、ミンコフスキーの時空図を書いて確認しようとする人がいるならば、座標軸の傾きの変化も通常のローレンツ変換と逆に考えてみてもらいたい(その延長で考えていくと、矛盾があるというご指摘メールはノーサンキューである。)。
さて、そもそもローレンツ収縮は、マイケルソン - モーリーの実験結果(エーテルの影響が検出できない)を説明し、なおかつエーテルの存在を認めるために立てられた。それは、「運動体はすべてその運動方向に収縮する」という仮説である。その仮説を理論的に完成させたのが、アインシュタインの特殊相対性理論である(考え方としては根本的に異なるが)。
今回の話の中で「エーテル」に変わるのは、「空気」だろうか? いや、違う。私はむしろ、速度そのものであると、考える。つまり、特殊相対性理論と同じである。スピードを出して飛んでいるという感覚、速度が与える感覚の変化、すなわち速度そのものが、「スキー場におけるhiraxの特殊相対性理論」を要請するのである。
今シーズン、スキー場でせっせとジャンプをする人がいるならば、ぜひ「スキー場におけるhiraxの特殊相対性理論」について考えてみてもらいたい。
このWEBへ来る人の中で、同時期に万座温泉スキー場にいた人はいるだろうか?12/11.12に万座温泉スキー場のプリンスゲレンデの下部でジャンプにいそしんでいたのが、私達の一行である。そして、その中の一人(ショートスキーでせっせと飛び跳ねていたヤツ)はこんなことをずっと考えていたのである。
さて、実際のタカノリ君(仮名)の飛距離がどの程度であるか知りたいと思う人も多いだろう。オマエらの主観的な評価でなくて、実測定した距離を教えろと思う人も多いに違いない。
「絶対的な基準など存在しないから、そんなことは私はわからない。」と言い放ちたいところだが、タカノリ君(仮名)の名誉のために書いておく。彼が飛んだ距離は、2m弱のスキー板で4本分はあった。実は、タカノリ君(仮名)の基準が一番正しかったのである。彼は、「やるときはやる有言実行の人」なのであった。
2000-01-23[n年前へ]
■偽札作りのライセンス 
このページはプリント禁止
「殺しのライセンス」を持つのはジェイムズ・ボンドである。コードネームで言えば、007である。殺しのライセンスを持つ人が本当にいるのかどうかしらないが、「偽札作りのライセンス」を持つ人はきっといるに違いない。
「そんなのは当たり前だ」という声も聞こえてきそうな気もするし、「まさか」という声も聞こえてきそうな気がする。そこで、そう思う理由を一応書いておく。
紙幣を識別する装置というのはたくさんある。例えば、自動販売機などその最たるものである。こういう紙幣識別機というものの動作確認には偽札が必要である。本物の紙幣(や硬貨)を「本物である」と認識する試験は割に簡単にできる。しかし、「偽札」を偽物だと検出するかどうかの試験をするには偽札を作って、テストしてみなければならない。
タヌキではあるまいし、「葉っぱ」を自動販売機に押し込んでみて、それを「千円札」とは違うと認識したところで何の意味もない。やはり本物とよく似ている「偽札」を使ってテストしなければならないだろう。そうなると、やはり「偽札」が必要になるわけである。
そういう「偽札」が必要となるからには、「偽札」を作る人も必要とされるだろう。まさか、「紙幣識別機」開発のために法を犯せ、と言うわけにはいかない筈である。ならば、「偽札作りのライセンス」がきっとあるに違いない、というわけである。
そんなわけで、きっと、「偽札作りのライセンス」は存在すると思うわけであるが、それでは「偽札を作って配る」ライセンスというのは存在するだろうか?紙幣(硬貨)識別装置の開発のためのテスト用に、「偽札」を作るのではない。「偽札」を配布するのが目的とするライセンスは存在するのだろうか?これが今回の問題である。
私はきっとあると思うのだ。何故なら私の手元にはそれらしき「偽札」があるのだ。本物のような、偽物のような紙幣があるのだ。
まずは、その「偽札」の画像を示してみる。以下に示す画像の内のどれが本物だか判るだろうか?あるいは、どこが違うか判るだろうか?
 |
 |
 |
「一目瞭然だぁ。」という声も聞こえるが、結構よく出来ている「偽札」だとは思わないだろうか?よく出来すぎと言っても良いほどである。福沢諭吉の目の辺りの拡大写真を示してみる。
 |
 |
 |
本物の(A)に対して(B)は実によく似ている。(C)の場合はハーフトーンパターンで細線などはつぶれてはいるが、それでもやはりよく似ている。(B)も(C)も明らかに本物の紙幣をスキャニングしてデザインを少し変えた後に印刷している。
根拠無しにそんなことを言うのも何なので簡単なチェックをしてみた。下の写真はそのやり方を示す写真である。ここでは、例として(A)と(B)の違いをチェックしているところを示す。
(A)の画像を「赤」チャンネルで表示し、その上に「緑」チャンネルで表示した(B)を重ねる。違いがあるところでは色ずれが生じるのですぐわかるのである。人間の目は色ずれには結構厳しいので、こうするとすぐに(A)と(B)の違いがわかるのである。もちろん、画像の差をとっても良いのだが、まず画像サイズや位置を合わせるまでは、今回のやり方の方が楽なのである。
例えば、下の画像では(A)と(B)の画像の大きさをまだ正確に合わせてないため、福沢諭吉の辺りでは違いが見られないのに対して、その他の部分では色ずれが生じている。また、福沢諭吉の下の部分に「ケンコーチョコレート」という表示があるが、これなど(A)と(B)の違いがあるので色ずれが生じていることがわかる。
 |
こういったテストをしてみた結果、本物の紙幣と「偽札」の間での簡単にわかる違いは、オリジナルの
- (A) 日本銀行券、一万円、日本銀行、紙幣番号、印影、大蔵省印刷局製造
- (B) 子供銀行券、五万円、子供銀行、ケンコーチョコレート、印影、大蔵省印刷局製造
- (C) 子供銀行券、一万円、子供銀行、紙幣番号、玩具印影、印刷所表示なし
私が面白いと思うのは、「大蔵省印刷局製造」の表示である。紙幣中央部下の表示である。これは他のもの(例えば、子供銀行券の表示)等と違いあまり目立たない部分である。この「大蔵省印刷局製造」の部分の拡大写真を示してみよう。
 |
 |
 |
(B)ではそのまま「大蔵省印刷局製造」と残っているが、(C)では文字部分は削除されている。
これは、(まさかとは思うが)デザインをしている時に、「大蔵省印刷局製造」の表示に気づかなかった、あるいは気にしなかったのだが、後でクレームがついたのではないだろうか?あるいは、後になって「これはちょっとマズイだろう」という判断をしたのではないだろうか?
そこらへんのことを想像すると、ちょっと面白い。
さて、「偽札」事件のよくある動機は技術者が自分の技術力を誇示しようとして作ってみた、というのが多いと聞く。私も実は作ってみたくてたまらないのである。「偽札作りのライセンス」が欲しくてたまらないのである。
2000-04-01[n年前へ]
■恋の力学 恋の相関分析編 
「明暗」の登場人物達の行方
「恋の力学」シリーズである。前書き編が登場したきりで、なかなか本編に入らない「恋の固体物理学」シリーズではない。今回は、
の続き、ということになる。以前、
の中で書いたように、恋の力学シリーズは夏目漱石の影響を多大に受けている。そして、同様に夏目漱石の影響を受けているシリーズがある。それは「文章構造可視化シリーズ」である。何しろ、「文章構造可視化シリーズ」は夏目漱石をきっかけとして、始まっているのである。また、シリーズの中の話を見ればわかるように、
- 夏目漱石は温泉がお好き?- 文章構造を可視化するソフトをつくる - (1999.07.14)
- 失楽園殺人事件の犯人を探せ- 文章構造可視化ソフトのバグを取れ - (1999.07.22)
- 「こころ」の中の「どうして?」 -漱石の中の謎とその終焉 - (1999.09.10)
- 「星の王子さま」の秘密- 水が意味するもの - (1999.11.15)
そのための準備として、まずは「文章構造可視化シリーズ」で作成した"wordfreq"をバージョンアップしてみた。その動作画面を以下に示す。
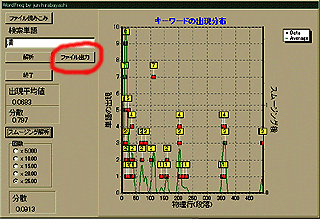 |
赤丸で示したボタンに「ファイル出力」と書いてあるのがわかると思う。つまり、文章中に「任意の単語」が出現した出現頻度を解析した結果をファイル出力する機能を持たせたのだ。1段落中に「任意の単語」が出現した数をテキスト形式で出力するようにしてある。このファイル出力結果を他のソフトに読み込めば、色々な解析ができるわけだ。いつものように、このソフトはここ
においておく。言うまでもないが、アルファ版の中のアルファ版だ。さて、今回用いるテキストは
でも登場した「明暗」である。そこで、「青空文庫」から「明暗」の電子テキストをダウンロードした。そして、バージョンアップした"wordfreq"で- 津田
- お延
- 清子
- 吉川
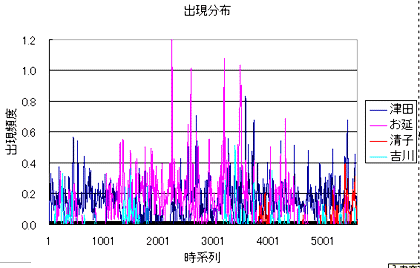 |
しかし、これだけでは、よくわからない。せいぜい「清子」が小説の後半(といっても、未完であるが)に登場しているなぁ、という位だろう。しかし、さらに解析を加えてみると、もう少し面白いことがわかる。
今回は、これらの登場人物間のお互いの関わりを調べたいのである。であるならば、これらの「登場人物」の出現分布の間の相関を調べてみると面白いだろう。互いの関係を示す「相関」を調べてみるのである。異なる「登場人物」が同じような出現をしているならば、それは無関係ではない。きっと、その登場人物の間には何らかの関係があるに違いないのだ。
そこで、「明暗」を時系列的に6つの部分に分けて、津田と他の登場人物の出現分布間の相関を調べてみたのが次のグラフである。
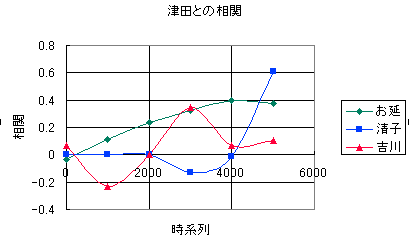 |
このグラフでは、横軸が時系列であり、縦軸が相関を示している。縦軸で上になればなるほど相関が高い、すなわち、「関係がある」のだ。「相関」は本人の場合で「1」である。だから、例えば最後の部分の清子の「0.6」という結果は関係がアリアリということを示しているわけだ。
また、「清子」と「吉川(ここでは夫人を意図している)」の相関が逆であることが面白いだろう。「吉川」が活躍(暗躍?)した後に、「清子」が登場するわけだ。
そして、この「明暗」が盛り上がっていくようすすら、見えてはこないだろうか?全く血の通っていないPCが解析した結果が、漱石の描こうとした「こころ」の動きを読みとっているような気が(少しは)しはしないだろうか?そして、このグラフの延長線上に、漱石の描くはずだった、「明暗」の結末はあるはずなのだ。
さて、このグラフを見ていると、
で計算した恋の多体(三体)問題の計算結果を思い出してしまう。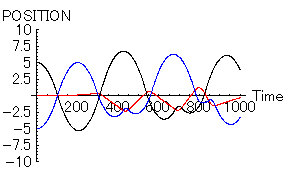 |
漱石は、きっと恋の三体問題を意識しながら「明暗」を書いたのである。だから、ある意味当然なのではあるが、科学と文学の一体化した世界が感じられ、とても面白い気分である。さて、この解析結果を元にして、まだまだ色々とやってみたのであるが、それは次回である。
2000-07-10[n年前へ]
■今日、欲しいなとふと思ったビデオ 
「事件記者コルチャック」と「探偵ナイトスクープ」
2000-11-21[n年前へ]
■いつまで続けるプロジェクトX 
もう、事件記者コルチャックの終わりの頃のようだ。いつまで続けるつもりだろう?関係ないが、アメリカンヒーローのビデオ等の入手方法の情報求む。