2001-09-27[n年前へ]
■ネットトラフィックの洪水の中で 
 事件後にニュースサイトのウェブマスター達がしたこと。必見。from お笑いパソコン日誌。
事件後にニュースサイトのウェブマスター達がしたこと。必見。from お笑いパソコン日誌。
別にヒーローを大量生産したいわけでは毛頭無くて、このウェブマスター達が
「そうして作られたページは、もしその会社のロゴが入っていなければ、パソコン初心者が作ったといっても信じてしまうくらいに素っ気無いものである。そしてウェブマスターはそんなページをダウン状態のサーバーに順次アップしていった。 」
という作業をしていた時の気持ちは「でも、少なくとも、今の仕事をきちんとこなしていく、それに尽きるなあ、なんて感じています。それがどんな地味な、力作業のような仕事であっても、です。だって今の私にできる、それがベストですもの。」というような感じだったのかな、とふと思った。埃にまみれたり、泥だらけになっていても、そんな時の人はきっと輝いてる、と思うのだけれど。(リンク)
2001-12-17[n年前へ]
■モンテカルロでビンゴ大会 
「幹事」のための確率講座
先日、会社の後輩が結婚したので、その結婚式の二次会が新宿で開かれた。会場は、花園神社近くにあるこじんまりとした地下のバーで、多分4〜50人くらいが普通に座ると一杯になる程の広さの店だろう。
そんな広さの店だったのだけれど、主賓のカップルの人徳だろうか、100人弱くらいの人達がその狭い店中に溢れていた。私達(『会社の先輩』と呼ばれる人達)はその一角に陣をとり、ビールを飲みながらカメラ談義などをしていた。EOS-1Digitalや50mmF1.0というレンズを前にして、私の手元にあるSpyzは段違いに情けなく、田代まさしの事件もあったせいで、恥ずかしさすら感じさせるほどだった。
そして、その二次会は四時少し前に始まったのだが、ほどなくビールとワインが進んだ四時半頃にはお決まりのビンゴ大会が始まり、私達もシートを片手に司会者の進行に耳を傾けた。
 説明も要らないだろうけど、読み上げられた数がシート上にあれば、 穴を開けて、穴が一直線に並べばビンゴだ |
(私を知らない人からは)クールと言われる私でも、何故かビンゴのシートを手にするとドキドキしてしまう。景品がどーしてもどーしても欲しいー、というわけではないのだけれど、やっぱりビンゴのシート片手にドキドキしてしまう。そんなドキドキは私だけではなくて、私の周りもみんなビンゴのシートを手にドキドキしているし、人間でなくてロボコップのようだと評された(評したのはワタシだが)こともある人でさえも、ビンゴのシートを手に司会者の声に耳を澄ませているのだから、きっとそれはみんな同じなのだ。
そして、そんな中、司会者は次々と数字を読み上げていった。が、何回新たな数が読み上げられても私の手元のシートはなかなか穴が増えていかないのである。クジ運が良いとは言えない私のシートがビンゴになかなか近づかないのはいつものことなのだけれど、ワタシの周囲の人もまた同じように全然穴が増えていかないのである。そして、それどころか実は会場全体の人がそうだったのである。全然「リーチ」と声を上げる人もいなくて、狭い会場で100人弱もの人がいるにも関わらず、この遅々たる進行状況はかなり異常なのではないか、と感じてしまうほどなのだ。
で、そのゲームの最中に手元のビンゴのシートを眺めながら私は考えた。なんで、こんなに時間がかかるのだろう?私だけでなく、ここに集う全ての人は不運の持ち主なのだろうか?不運の持ち主が100人集まるとは、これは一体何事だ?不運の会か?と、結婚式の二次会にはとても相応しくない想像さえしていた。
で、そんな相応しくない想像をしながらそのシートを眺めていると、ふと気づいたのである。「ん?99?えっ?きゅーじゅきゅうー?」 この不安な気持ちは何だろう?手元のシートは5x5で高々25個の数字しかないのに、書いてある数は99までもある。ということは、呼び上げられる数字はきっと01から99までの100個。ということは、呼び上げられる数字に対して、手元のシートの「数字」の数は1/4程しかない。それでは、そもそもシート上になかなか穴が開いていかないのではないだろうか?そのペースで一体何回数字を読み上げれば、シート上で穴が一直線に並ぶのだろう?そして、あの何個もある景品達は一体何時になれば全部売れていくのだろう?う〜ん、ビールが回った頭では全然判らないぞー。いや、きっとシラフでも判らないぞー、そして、貸切の時間を考えるときっと司会者もドキドキしてるぞーと思ったのである。
結局、最初にビンゴになった人が出たのが、ビンゴを始めてから20分以上過ぎてからだったと思う。そして、10個ほどの景品が配り終えられたのはビンゴが始まって一時間程した頃だった。つまりは、二次会がお開きになるくらいの時間だった。司会者はかなりヒヤヒヤしていたようだった。
そして、帰りの電車の中で私は考えた。もしかしたら、ビンゴ大会を開く幹事には、確率統計の知識が必要とされるのではないか、と。何人の人達が会場にいて、景品は何個あって、ビンゴのシートには1から何までの数が書かれているから、一分に一個の数字というペースで読み上げていけば、ビンゴ大会にかかる時間は何分だ、と概算できるくらいでないともしかしたらマズイのかもしれない、と思ったのである。少なくともヒヤヒヤしないためには、そんな概算をしておくのも良いかもしれない、と思ったわけだ。
で、そんな司会者・幹事のために、今回試しにビンゴの確率論を計算してみることにした。といっても、私は確率・統計がどうにも苦手なので、モンテカルロシミュレーション(別名下手な鉄砲も数打ちゃ当たる法)である。つまりは、何回もサイコロを振ってシミュレーションしてみただけの話である。PCの中で繰り返し、ビンゴ大会を開催してみただけなのである。ビンゴというギャンブルの確率を計算するのだから、それはもうモナコ王国誇るモンテカルロ・シミュレーション以外ないと思うのである。
そんなわけで、下に示すのが「何回目でビンゴになるか一万回試行したときのモンテカルロシミュレーションを行ってみた結果」である。実際にビンゴ大会を一万回したらものスゴイ時間がかかるが、PCの中だったら一瞬ですむのが素晴らしいところである。ちなみに、ビンゴのシートの条件は、シートに書かれている数字が
- 01〜24
- 01〜49
- 01〜74
- 01〜99
 |  |
 |  |
これを見ると、例えば、シートに書かれている数字が01〜24までの範囲の場合は、12回目位で半数の人がすでにビンゴになっていることが判る。一分に一個の数字というペースで読み上げていけば、5分過ぎには半数が終了している、というペースである。かなり速いペースである。
それに対して、シートに書かれている数字が01〜49までの範囲の場合ともなると、25回目位でやっと半数である。とはいえ、一分に一個の数字というペースでも、12,3分で半数がビンゴだから、これもやはりかなり速い進行だ。
ところが、さすがにシートに書かれている数字が01〜99までの範囲の場合ともなると、半数がビンゴになるのが、60回目位なのである。先程の数字を読み上げるペースであれば、時間にして30分である。景品の授与の時間などを考えると、かなり時間がかかってしまいそうだ。きっと4,50分ほどはかかることだろう。実際、先日のビンゴ大会はその程度の時間がかかっていたわけである。
そこで、試しに先日のビンゴ大会と同じ人数でモンテカルロ・シミュレーションをしてみた結果が下である。会場に100人の人がいた場合のビンゴになる人の回数(時間)に対する割合である。
 |  |
 |  |
この結果だと、会場に100人の人がいた場合、最初のビンゴになる人は
- シートに書かれている数字が01〜24までの範囲の場合 → 4回目
- シートに書かれている数字が01〜49までの範囲の場合 → 8回目
- シートに書かれている数字が01〜74までの範囲の場合 → 10回目
- シートに書かれている数字が01〜99までの範囲の場合 → 27回目
というわけで、これからの忘年会・パーティーシーズンに向けて、「幹事」は電卓を叩いて会費の計算をするだけではなくて、確率・統計の知識もあると便利かもしれない、モンテカルロでビンゴ大会の予行練習をしてみるのも良いかもしれない、と思ったのである。とはいえ、そんな確率統計を計算し尽くした「幹事」もちょっとイヤかも、とビールが回った頭で想像したりしたのだった。
2001-12-24[n年前へ]
■サンタが街にやってくる 
複数サンタクロースの巡回問題
簡易に書き直した2011年版もあります。
幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで(高原の診療所なのだから大して違いはないのだけれど)、とても不思議だった。
さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。
知らない人のために書いておくと、「巡回サンタクロース問題(TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが
- サンタクロース研究
- ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )
そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。
まず、始めに問題提起をしてみよう。
「果たしてサンタは一人なのか?」
どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。
そこで、まずはサンタの歴史から調べてみると、Santaさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。
とはいえ、Santaさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか?
また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
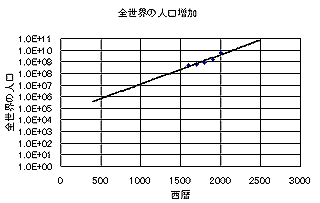 |
St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。
サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。
子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 |
どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。
先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。
そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。
それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
一例として、サンタが1,2,10人の場合を示してみる。
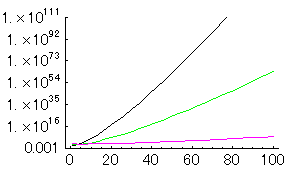 |
このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。
実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。
このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。
ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。
それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。
ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。
もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。
こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。
サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。
2002-01-20[n年前へ]
■徳川埋蔵金殺人事件 
超論理特許ミステリー「狩野埋蔵金の埋蔵場所を解読し発掘する方法」
ワタシの勤務先では「一年に*本特許を書くべし」という恐ろしいノルマがある。もちろん、こまめに書いていれば何の問題もないのだけれど、他の仕事にかまけてついつい後回しにしていたりすると、年末や期末には特許をまとめて書かなければならなくなる。架空の物語を量産する小説家のように、架空の実験データを描き整理し、架空の特許を量産しなければならなくなるのである。
いつものごとく、昨年末もそうだった。年末の最後の二三日は特許書きで追いつめられ、しかも書き上げられずに、できの悪い小学生のように、家へ書きかけの特許を持ち帰って、正月休みに特許を書かなければならなくなったりしていたのである。そんなわけで、正月番組を見ながら、特許庁の電子図書館のサイトにアクセスし特許調査をしつつ特許を書いていた。が、正月番組などを眺めているせいか、どうにもマジメに特許が書けなかったりするのである。いつしか、ビールを飲みながら仕事とは全然関係無い特許公報を眺めていたりしたのである。
今回、紹介する特開2001-42765「狩野埋蔵金の埋蔵場所を解読し発掘する方法」という公開特許公報もその一つである。キャッチーな名前で想像つくとは思うが、なんとこの特許出願はいわゆる赤城山徳川埋蔵金の場所を発掘するための特許なのである。世に出される特許は数多く、埋め立てゴミの数より多いくらいかもしれないが、そんな中でも「埋蔵金の隠し場所を解読し発掘する方法」なんて特許は見たことがない。歴史ミステリー、暗号ミステリー、そして、ご当地モノミステリーなどが好きなワタシは思わず目を奪われ、その特許を読み始め、そしてこの超論理特許ミステリーの世界に引き込まれたのだった。
そして、この特許のあまりの素晴らしさに今回こんな感想文を書いて、世の中にこの超論理特許ミステリー特許を広めたいと思うのである。そして、さらにはこの感想文を読んだ人が特許フォーマットに慣れ親しみスラスラと特許を書けるようになり、ワタシのように特許を書き残しで苦しむ人が減ることを強く望む次第なのである。
さて、特許では、まず「発明の名称」を書かなければならない。この特許でももちろんそうだ。というわけで、
「発明の名称」 狩野埋蔵金の埋蔵場所を解読し発掘する方法
何とも、キャッチーな名前である。これが火曜サスペンス劇場であれば、「徳川赤城山埋蔵金全裸殺人事件2 湯けむり露天風呂で美人女子大生が消えた!村に残る伝説が不気味に今よみがえる!」くらいにはパワーアップすることだろうが、特許の書類としては十分に魅力的である。この名前を見れば、誰しもワタシのようにこの特許の世界に引き込まれるハズである。
そして、次に「どんな範囲のこと」を特許として宣言するかを書くわけだ。これを請求項と呼ぶが、この特許はもちろんこれだ。
「請求項」 従来一般に赤城山徳川埋蔵金といわれている黄金の埋蔵場所を発見・発掘すること
なんと、赤城山徳川埋蔵金といわれている黄金の埋蔵場所を発見・発掘してしまうのである。特許を書いて大金を手に入れるという話はたまに聞くが、特許を書いて埋蔵金を手に入れるという話は聞いたことがない。まさに、夢というか、男のロマンというか素晴らしい特許なのである。
そして、次に「従来の技術」というセクションが続く。つまり、従来はこんな問題がありますよ、こんなに不便だったのですよ、ということを書くのである。それに対して、今回書いたこの技術はそんな「従来の課題」を解決できて、価値があるのですよ、と訴えるのだ。そこで、この特許は説く、
「従来の技術」 従来の技術は、解読に科学性が不足していたために、経済効果の悪いものであった。…暗号のかたちで示されている埋蔵金を資源として再利用するためには、闇雲に探したのでは経済的に成り立たないので技術とは言えない。埋蔵金の探査技術が発達すれば、埋蔵金の発掘は夢や学問でなく産業になるであろう
なんと、これまでの発掘を「技術とは言えない」と喝破しているのである。かつて、近所の埋蔵金伝説に、電子ブロックの金属探知器を頼りに闇雲に探そうとしていたワタシなどは、「あぁ、ゴメンナサイ、ゴメンナサイ…」と謝らなくてはならないような勢いなのである。この作者発明者は埋蔵金の探査技術が発達すれば、埋蔵金の発掘は夢や学問でなく産業になるとまで謳いあげるのだった。今さっき、埋蔵金探しは「夢で男のロマンだぁ」と書いたワタシはさらに「ゴメンナサイ、ゴメンナサイ…」と謝らなければならないのである。
さらに、従来の「埋蔵金探し」を箇条書きに上げ、
- 勘で場所を決めて、縦穴を掘り、さらにいくつもの横穴を掘ったり、ブルトーザーで土を押しのける
- 百年にもわたり、長期間諦めずに掘る
しかし、そんなミステリー特許に引き込まれていくワタシの心の中のツッコミなど知る由もなく、この埋蔵金小説許では、引き続き具体例を挙げて特許の内容を説明していくことになる。それが、次の「実施例」である。具体的な資料群をもとに、埋蔵金発掘に迫るストーリ〜が書き示されている。
が、この資料群がスゴイのである。何しろ、こんな感じなのだ。
- 資料A 「常習赤城におよそ三百六十万両。古井戸を掘ることを手がかりとすべし」という水野家に伝わる遺言
- 資料B 「寺の床下から発見された方位図・地図・暗号文書」
- 資料C 「空井戸から発見した銅板と像」
- 資料D 「黄金埋蔵はアッという間にされたらしい、という地元住人のウワサ」
 |
 |  |
しかも、資料Aの「常習赤城におよそ三百六十万両。古井戸を掘ることを手がかりとすべし」という遺言に対しては、「ここで疑問に思うのは、義父が何故もっと詳しく埋蔵場所を教えなかったのか」などと死者にムチ打ち、マジメなのかそれともツッコミ?と言いたくなるような感想・疑問を書き、この疑問に対して延々2ページに渡り超論理的考察、超心理的考察を加えることで、ついには「埋蔵金は七つの古井戸に埋蔵されたことになる」と、超論理科学的に鉄槌結論を下すのである。
そして、下に示す「寺の床下から発見された方位図・地図・暗号」を基に、黄金分割を始めとする数学的考察などを駆使し、埋蔵金の位置を推定する。しかも、単に推定するだけでなくて、経済的・効率的に発掘をするために埋蔵金の位置の計算誤差を延々と論じて、ついには誤差50cm〜7m弱だと推定するのであった。なるほど、この歴史ミステリー小説特許は単に技術特許にとどまらず、経済を見据えた経済ミステリー特許でもあったのだ。「埋蔵金の発掘は夢や学問でなく産業になる」のだ。
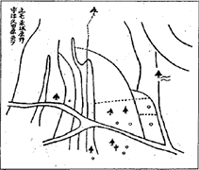
さて、この埋蔵金ミステリーで指し示された「埋蔵金の埋まっている七つの古井戸」がどこであるかを知りたい人も多いだろう。ということで、特許の図を重ね合わせ、埋蔵金の埋まっている七つの古井戸の場所をプロットしてみたのが、次の図である。どの辺りか判らない人のために、広域地図をリンクしておくとここら辺りということになる。
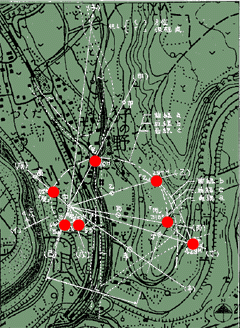 |
さて、この特許の最後には「なお、この辺りは便利な住宅地向きの環境になりつつあるので、住宅が建設される前に発掘することが望ましい」と
と産業としての指針まで描きつつ筆をおくのである。
どうだろうか、面白いミステリー小説特許だったのではなかろうか?そして、特許なんて簡単に書ける、と思った人もいるのではないだろうか?そして、どんどん特許を書きたくなる、と思う人も多いに違いない。で、ワタシは思うのだ。できれば、できることであれば、その書いた特許をワタシにも少し分けて頂いて、ワタシのノルマを少しでも減らして欲しい、と強く強く思うのである。