1999-03-30[n年前へ]
■ペットボトルロケット 
天まで昇れ
-天まで昇れ-
先日、2月21日、糸川英夫が死去した。ロケットを研究し続け、日本のロケット技術を築き上げた人である。
ISAS(宇宙科学研究所)の歴史(http://www.isas.ac.jp/info/history/index-s.html)
そこで、私たちが簡単に打ち上げることのできる、ペットボトルロケットについて考えてみたい。ペットボトルロケットは素晴らしい科学おもちゃだ。ロケットが大気中を飛ぶときと、宇宙空間を飛ぶときの原理の違いを的確に体現していると思う。それは、ペットボトルの中に水を入れてあることだ。ペットボトル中に水を入れることで、革命的ないくつかの効果があると私は思う。挙げてみると、こんな感じだ。
- 空気と水の粘性の違い->水の方が長時間にわたり一定の噴出量にしやすい。
- 気体(空気)と液体(水)の圧縮性、質量の違い->
- 空気を噴出する場合には、ロケットの前後の圧力差が推進力を支配する。
- 水を噴出する場合には、反作用力(運動量保存)が推進力を支配する。
空気のほうは温度が違うと結構違う。摂氏0度で1.293kg/m^3であり、100度で0.946kg/m^3である。もちろん、気圧が違えば、それに比例して体積は大きく変わる。
結局、空気と水とでは質量が約1000倍違う。だから、ペットボトルロケットが後ろから水を噴出する場合には、空気の場合に比べて、1000倍もの反作用力を受けるのである。つまり、ロケットは1000倍の推進力を持つことになる。ただし、空気の場合には、ペットボトル中で数気圧分圧縮されているので、質量も数倍になる。したがって、正確には1000倍の数分の一ということになるだろう。
逆に、ロケットの前後の圧力差を考えてみる。、空気の場合には、前後で数倍の圧力差が生じるだろうが(WEBで調べると5-7倍位が通常上限のようだ)、水の場合には前後での圧力差はほとんどないだろう。だから、水を噴出する際にはこれによる推進力はほとんど働かないだろう。しかし、空気を噴出する際にはこの圧力差によりロケットは進むことになる。真空中ではこの方法では推進力はほとんど働かない。
こういった違いをもとに子供(といっても高校生位か)に宇宙でのロケットの原理を説明すると面白そうだ。これら推進力の違いは、とても大きいと思う。
かつては、セルロイドを使った小さなキャップロケットの時代だった。今は、ポリエチレンテレフタラート製の大型ロケットの時代に変わった。
今日は久しぶりに雪が降った。「雪は天からの手紙である」と言ったのは、雪を研究し続けた中谷宇吉郎だった。ならば、私たちが打ち上げるペットボトルは天へと届けるロケットだ。空へ高く届くように、私たちはそれを打ち上げ続ける。いつか、私たちのロケットは天へ昇る。
 |
2000-06-07[n年前へ]
■毛髪力のガウスの法則 
ハゲの物理学 「第五の力」編
現代の物理理論では四つの力が取り扱われている。その「四つの力」を示してみると、次の
- 重力
- 電磁気力
- 弱い力
- 強い力
ところで、これら「四つの力」に加えて、さらなる「第五の力」が測定されたという報告がされることがある。しかし、(少なくともこれまでは)それらはいずれも眉唾モノの実験ばかりであった。しかし、誤解されることを承知の上で、私も「第五の力」の提案をしてみたい、と思うのだ。
と書くと、鼻で笑う人がいるかもしれない。物理が大好きな人は私を小バカにするであろうし、物理を好きでない人はとたんに興味を失うであろう。しかし、そんな方々も少しばかり私の意見に耳を傾けるべきである。少なくとも、男性にとっては、この「第五の力」は重要な問題であるはずなのだ。いや、私は決して「理論物理=男性の領域」などと言うつもりはない。もうとうそんな考えはない。しかし、この私が提案する「第五の力」に限っては女性よりも男性にとって重要な「力」なのである。
私が提案する「第五の力」は、その名も「毛髪力」である。もう、おわかりのはずだ。これぞ、男性の人生をかけた大問題、「ハゲ」に関する問題なのである。「毛髪パワー」が「第五の力」なのである。
さて、そもそも今回「毛髪力」という「第五の力」に関する理論を提唱するにあたって、素晴らしき先達の研究があったことをここに書いておきたい。それはfreddie氏による「頭髪におけるキルヒホッフの法則」という素晴らしい研究報告である。「ボクテレビ」の2000/05/25に報告されている「物理と頭髪」の中にその詳細は記されている。
freddie氏は女性の視点から、女性のウィッグに関して、
そこで、僕は束ねられた髪の毛に関する基本法則をここに記したいと思います。と記している。私はこの「頭髪におけるキルヒホッフの法則」からインスピレーションを受けて、さらに男性の視点から理論を展開したい、と思うのである。
- 頭髪におけるキルヒホッフの法則:
「髪の毛を束ねる部分に頭皮側から入る髪の本数と毛先側へ出て行く髪の本数は同じ。」
先の「頭髪におけるキルヒホッフの法則」では、「頭皮側から入る髪」とあっさり書かれているが、男性の場合「頭皮側の髪」がそもそも無い場合がある。そう、「ハゲ」である。こう、私が書くのは、「毛髪力」は私にとって、人ごとでないからだ。自慢ではないが、私の髪はストレートのサラサラである。と言うと、羨ましがる人もいるかもしれない。しかし、それは違う。女性ならともかく、男性の場合は違うのだ。そう、絶対に違うのだ。何しろ、ストレートのサラサラヘアーは「ハゲへの片道切符」なのである。「恋の片道切符」はロマンチックであるが、「ハゲの片道切符」はそうではない。断じて、違う。違うのだ。
そもそも何故、我々の「長い友達」であるはずの「髪」が消えてなくなるのだろうか?そして、さまざまな「ハゲ頭」は一体どのような理由で発生するのであろうか?これらの疑問について、明快に答えた例は未だかつてない。ましてや、それを物理学的に考察した例は未だない、と思う。そもそも、毛髪とは何であるか明快に答えられる人がいるだろうか?いや、いないはずだ。
しかし、私はその答えを今日ついに見つけたのである。それが、「毛髪力」なのだ。この「力」が全ての物理現象を決め、我々の人生の喜怒哀楽を支配しているのである。毛髪、すなわち、「髪の毛」は「毛髪力」により発生する物理現象だったのである。
例えば、電磁気力で言えば、基本をなす方程式はマックスウェルの方程式である。次に、マックスウェルの方程式の一部を積分形で示してみると、このようになる。
![]()
- Kami!Home Page:ElectricField ( http://home.att.ne.jp/gold/kamikawa/electricfield/elefield.htm)
 |
この画面を見れば、一目瞭然だと思う。次の絵との相似性を感じるはずなのだ。
 |
この絵は頭皮から伸びる毛髪を示したものだ。電荷から伸びる電気力線と毛髪は実によく似ているものなのである。電磁気力と毛髪力は実によく似ているのだ。
ここで、先程の電磁気力と同じように、毛髪力に関するマックスウェルの方程式の一部を積分形で示すと、以下のようになる。
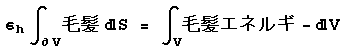
さて、さらに話を進めれば、重力であればそれは「重力子 = graviton」の交換により作用する。また、電磁気力であれば、それは「光子= photon」の交換により作用する。私は「毛髪力」に関してもこのような説明がつけられるのではないか、と考えている。
「重力子、光子」、すなわち、graviton,photonの名前の由来からすれば、その作用子は「毛髪子= moukon」と考えるのが自然だろう。私は日本語における「毛根」という言葉はこの「毛髪力」の作用子「moukon」の訛ったものではないか、とすら考えているのである。言語学的にも、「毛髪力」の妥当性が裏付けられた、と言っても良いだろう。
さて、毛髪は大抵の場合時間の経過にしたがって、少なくなっていく。いや、端的に言えば「ハゲ」ていく。毛髪力が低下していくのである。これも、先程の毛髪力のガウスの法則から考えれば、頭部内部の毛髪エネルギーが低下していると考えるのが自然である。ここで、私は、「頭部内部の毛髪エネルギーが低下」毛髪子の減少によるものだと考えている。毛髪子は何らかの変化により、他の粒子に変化するのだろう、と私は推察しているのだ。
「たいていの場合、ハゲた頭は光り輝く」ということから推察するならば、「毛髪力」は「光」に変化すると考えるのが自然である。すなわち、毛髪子は光子に変化していくのではないか、と私は現在のところ想像しているのである。毛髪力と電磁気力は表裏一体のものなのである。
 |  |
今回は、「第五の力」について論じてみた。唐突な話で判りにくいかもしれないが、この「ハゲの物理学」は私の人生と共に、まだまだ続く予定である。これから、先話がどう進んでいくかは私にも判らない。それは、私にとって吉と出るか、凶と出るか不安なところだ。実際のところ、それは誰にも判らないだろう。「毛髪力」の研究は今始まったばかりなのである。
2000-06-29[n年前へ]
■オッパイ星人の力学 
胸のヤング率編
本WEBサイトは「技術系サイト」というジャンルに分類されることが多い。が、実際にはどうも変な話題も多いように思う。しかし、私の観察によれば技術系サイトと呼ばれるところには必ずこの手の話が転がっているのである。実際、究極の技術系サイトの「Fast&First」でもというような素晴らしい話題はいっぱいあるし、同様に至高の技術系サイトである「今日の必ずトクする一言」の中でもという絶品の作品達が飾られている。
いや、つまり何が言いたいのかというと、変な話を書いてしまったことを正当化したいのである。技術系サイトには「とても身近なナゾ」への探求話が欠かせないのだから、変な話を書いたけど、勘弁しておいて欲しい、と言いたいのである。間違ってもエロサイトには分類して欲しくないのである。さて、どんな話かは下を読んで頂くことにして、もう少し言い訳を続けたい。何と言うか、この話を書き終えて何故か言い訳なしにはWEBに出せないような気持ちに、私はなっているのである。いっそのこと、この話は封印しようかとも考えた。しかし、先に示したように究極・至高の技術系サイトにもこういった?類の話があることに勇気付けられ、せっかくなので公にしてみることにした次第である。
以前、
で「できるかな?」読者の好みを調べてみた。それがこの下の円グラフである。 |
この円グラフから引っ張った部分は「エロ」である。これは、「IO = アイオー」ではない。「エロ= えろ=すけべぇ」である(前にも書いたけど)。 かように、「エロ」に興味を持つ人は多い。例を挙げるならば、「オッパイ星人」という言葉があるくらい、男の中には女性の胸に興味を持つ人が多い。私の友人の中には、ことあるごとに「おぉっ!!」と言いながら、通り過ぎる女性の胸を眺めるような輩までいるのである。しかもメガネをポケットからすばやく取り出し、サッとメガネをかけながら眺めるのである。まるで、ウルトラマンのセブンに変身する瞬間のモロボシダンなのである。「ウルトラセブンか、オマエは!」とか「モロボシダンがオッパイ星人に変身してどないすんねん!」と突っ込みたくなるほどである。
とりあえずこういう「オッパイ星人」のために、今回は「オッパイ星人の力学」について考えてみたい。具体的には、「バスト(なんか気恥ずかしいので言葉を変えた)の力学」について考えてみることにした次第である。
それでは、バストの力学について考え始めることにしよう。今回は、まずバストの基礎特性を調べ、次回にその運動力学について考えてみる予定である。
最初に、基本的な知識からだ。TVを観ていると、よく「Fカップアイドル」というような言葉を聞く。その言葉はよく耳にするのだが、実際のところその意味は知らなかった。そこで、調べてみると、ブラジャーのカップサイズは次の表のようにして決まるという。
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| アンダーバストと トップバストとの差 | 5.0 | 7.5 | 10 | 12.5 | 15 | 17.5 | 20 | 22.5 | 25 | 27.5 | 30 | 32.5 | 35 |
胸のバスト直下の部分の胸囲 = 「アンダーバスト」と、バスト部分の胸囲= 「トップバスト」の差からブラジャーのカップサイズが決まるわけだ(って今知っただけの知ったかぶりだけど)。Kカップなんてのもあるなんて驚きである。いやぁ、知らなかった。
しかし、「アンダーバストとトップバストとの差」が判っただけではバストの力学について考えるのは難しい。もう少し、取り扱いやすい量に変形させたい。そこで、次のような図を考えてみた。これは「胸部の断面図」である。上方向が人の前面方向である。
 |
バストを「半球状の物体」と仮定して、その「半球の半径 = r」を計算したいのである。そうすることで、バストの形状を計算しやすくなるのである。現実問題としては、バストがそうそう「半球状の物体」になるわけはないだろう。しかし、今回はとりあえず理想のドーム形状のバストを計算してみる、ということで許してもらいたい。
さて、上の極めて大雑把な近似をしまくりの図を見て頂くと判るように、
アンダーバスト = 4r + 4r + 2 胸のベース部分の厚さであり、
トップバスト = 2 r + 2 π r/2 + 4r +2 胸のベース部分の厚さである。したがって、
「アンダーバストとトップバストとの差」 = ( 2 r+2π r/2+4r+2胸のベース部分の厚さ)と計算してやることができる。そのようにして、計算した「胸のカップ数とr(cm)」を示したものが下の表である。ただし、実際には胸囲はそもそも下へ行くほど小さくなっているだろうから、アンダーバストはトップバストよりも胸のベース部分が35%小さいとして計算してみた。
- ( 4r+4 +2胸のベース部分の厚さ )
=2 r+2πr/2-4r
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| r | 2.8 | 4.3 | 5.7 | 7.1 | 8.5 | 10 | 11 | 13 | 14 | 16 | 17 | 19 | 20 |
これをグラフにしたものを下に示す。ほぼ直線的にバストのサイズが増加しているのが判ると思う。
 |
例えば、AAAカップだと半径2.8cmの半球状の物体だ。まるで、スーパーボールである。これなら、ブラジャーはいらないだろう。それが、Kカップともなると半径20cm程になる。ちょうどメロンを半分に切った感じだろうか?これはかなり、デカイ。
このr(cm)さえ計算できれば、あとは物体形状も体積もわかる。体積が判れば、当然のごとく重さも計算することができる。というわけで、次は重さについて考えてみよう。何しろ、バスとの運動力学を考えるならば、どの程度の質量を持つかどうか考えることは避けて通れないのである。
バストのほとんどの部分を占めるのはきっと脂肪だろう。脂肪の密度は水とほぼ同じだろう。そこで、脂肪の比重が1g/cm^3であるとして計算してやると、「胸のカップ数と胸一個あたりの重さ(g)」は以下のように計算することができる。(実はこの計算には後の松坂季美子の胸の重さに合わせるための定数、季美子定数を乗してある。)
| カップ | AAA | AA | A | B | C | D | E | F | G | H | I | J | K |
| 胸一個あたりの重さ(g) | 8.9 | 30 | 71 | 140 | 240 | 382 | 570 | 810 | 1100 | 1500 | 1900 | 2500 | 3100 |
なんと、Kカップでは「胸のカップ数と胸一個あたりの重さ(g)」が3000g= 3kg程もあるのだ。新生児が二人胸にぶら下がっているのである。この数字がホントなら大変な話だ。肩に負担がかかりんまくりである。1.5リットルのペットボトルを4本も胸にぶら下げているのだから、これは大変だ。なるほど、ブラジャーは必需品である。
上の表をグラフにしたものが下である。
 |
バストの質量は体積に比例する、すなわち、バストのサイズ( =長さ )の二乗に比例する。そこで、このような形状のグラフになるわけである。このグラフを眺めていると、Dカップ辺りを境にして、それより大きくなると胸や肩にかかる負担がシャレにならないくらいの大きさになると推測される。
ところで、地表にいる限り、当然バストも重力の影響を受ける。いや、むろん地表でなくても重力の影響は及ぼされるわけだが、そういう話は今回はおいておく。とりあえず、六本木を歩いている彼女も、ロサンゼルスにいる彼女も重力の影響を受けるのである。重力を受ければ、当然バストは重力で引っ張れる方向に垂れ下がってしまう。その様子を示したのが、次の図である。ここでは、「胴体から垂れ下がるバスト」を単純に「重りとバネで表すことができるモデル」だとしてみた。
 |
さて、一般的にバネの特性はフックの法則により
ここまで来れば、あともう一歩である。この式のkすなわち「バストに関するヤング率」を調べるだけである。「バストの垂れ具合」と「バストの重さ」を同時に計ってやれば良いのである。そうすれば、残るただ一つの変数、「バストに関するヤング率」を計算することができる。いやぁ、簡単、簡単....
といっても、実際のところここが一番苦労した。「バストの垂れ具合」と「バストの重さ」を同時に計らせてくれる人なんかどこにもいないのである。当たり前である。
そこで、ネットで検索をかけまくること数時間、ついに私は見つけたのだ。
そして、その質量 一個1kg!」
科学の徒として、私が丁寧に観察した結果、松坂季美子の「バストの垂れ具合」は約10cmであることがわかった。いや、もちろん科学の探究心のためであって、それ以外の気持ちはなかったことをここに誓っておこう。
その苦労の結晶のデータが、
- 松坂季美子はGカップ、バストの重さ=1kg、バストの垂れ具合10cm
この境界条件さえあれば、「バストに関するフックの法則」を完全に解くことができて、「バストに関するヤング率」も導き出すことができるのだ。ちょちょいのちょい、である。
その「バストに関するヤング率」を用いて計算してみた「胸のカップ数とバストの垂れ具合(cm)」を次に示してみる。
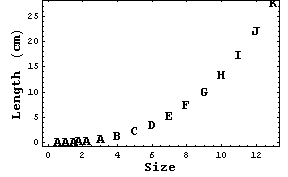 |
バストの「カップ」サイズの三乗に比例して、「バストが垂れていく様子」がよくわかると思う。この物理形状は「カップ」サイズに比例して、「バストの垂れ具合」は「カップ」サイズの三乗に比例するというデータを用いることにより、「究極のバストサイズ」を導き出せるのではないか、と私は考えているのである。が、それはまたいつかの話題と言うことにして、話を続けたい。
ところで、「バストに関するヤング率」は常に一定ではない。「おばあちゃんの垂乳根」を想像して頂けばわかるように、年をとれば「バストの垂れ具合」は大きくなるのである。
というわけで、さっきの計算結果をもっと若い条件、すなわちもっとヤングなヤング率で計算してみたのが次のグラフである。
 |
赤のもっとヤングなヤング率で計算してみた場合には、バストには張りがあって、バストの垂れ具合は小さいことがわかると思う。
さて、今回はバストの基礎特性を調べてみた。次回、この「バストに関するフックの法則」を用いて、「オッパイ星人の動力学」について考えてみたい、と思う。
追伸 : この話を書き上げた後に、恐る恐る回りの人に感想を聞いてみた。すると、
と言われてしまいました。ハイ、申し訳ありません。その通りでございます。返す言葉もありません。「こんなの作るくらいなら、
男の人のヤング率でも計算しなさいよ。」
2001-01-13[n年前へ]
■オッパイ星人の力学 第四回 
バスト曲線方程式 編
先日、父から封書が届いた。二十一世紀にもなったというのに、e-mailでもなくて封書が届いたのである。これは、やはりアレだろうか。いい年にもなってるのに、クダラナイWEBサイトを立てているデキの悪い息子を厳しく叱るためだろうか?しかも、そのクダラナイWEBサイト(しかも、有害公式認定サイト)の名前が自分の名前(hirax)だったりするからだろうか?それとも、「本が出たなら送れ」とは言われても実は送りたくなかった「あの本」を、少し前に父に送ってしまったからだろうか?いや、それとも…そんなこんなでドキドキしながら封筒を開けると、記事のコピーが二つ入っていた。他には何も入っていないのである。一体これは何の記事だろう?と思いながらそのコピーを眺めてみた。すると、まずひとつは去年の12月25日付けの毎日新聞の科学欄である。二十一世紀を専門家達が予想した記事の横に「究める」というコーナーがあって、そこに「女性の胸と男性の好みの進化的関係は?」というインタビュー記事があった。そして、その記事が蛍光ペンでマーキングしてあったのである。
これは一体、どういうことなのだ?と頭の中がグルグル&複雑な気持ちになりながら、とりあえずその記事を読んでみた。すると、この記事がとても面白い。インタビュー中の
ヒトは異性をどう選ぶのか?そんな疑問から女性のバストと弾性の好みに進化的関係があるかを研究している。という東大大学院の東海林さんの語りもとても面白いし、バストサイズを5段階に変えた女性の合成写真を使い、男子学生300人にアンケートしたという実験とか、巨乳好きの性格が父から受け継いだものであるかを調べるために、父子間で性的好みが伝達されるかを調べる、などの話もとても面白い。最高である。(中略)小さいバストほど魅力的だと母に教えられて育った。しかし、大きいバストが好きな男性がいることに気付いて驚き、「なぜ」と考えたのが研究のきっかけだった。(中略)「大きいバストが本当に普遍的に好まれるかを知りたい。控えめなバストが淘汰されてしまうとは考えたくないから」と話す。
そして、父からの封筒に入っていたもう一つの記事は宇宙科学研究所の新聞の中の宇宙基地利用研究センターの黒谷氏の「Anti-Gravity」というエッセイだった。なんでも、Anti-Gravityという化粧品があって、
それは顔の皮膚のコラーゲンに皮膚がたるまないようにするというものらしい。顔の皮膚にハリをあたえて、顔のたるみを防ぐのである。顔の皮膚のたるみ元をたどれば重力のせいだから、「anti-gravity= 無重力」化粧品ということになるわけだ。じゃぁ、このAnti-Gravityを体中に塗れば、バストやヒップが垂れるという女性の悩みもなくなるのではないか、と「無重力における生物の専門家」である黒谷氏は書いていて、参考文献に本サイトが挙げられていたのである。
うむむ、世の中には巨乳の科学について進化論的に研究している人がいたり、オッパイの力学について考え(てみたりもす)る無重力生活の専門家もいるのだ。これはマズイ。油断している場合ではない。私もオッパイ星人研究をもっと真剣にしなければならない。父はきっと私に「研究の厳しさ」を教えようとしたに違いないのである。私の父はこれまでの「オッパイ星人の力学」を読んで、美味しんぼの海原雄山風に「うわあっはっ、こんなものでオッパイ星人の力学だとは笑止千万!」位のことを言ったに違いないのである。
しかし、それだけではない。「二十一世紀、小さいバスト、大きいバスト、無重力、皮膚、オッパイのたれ」というヒントを与えてくれたのである。ここまでされて何かを書かなくて何としよう。オッパイ星人研究の手は一瞬たりとも休めてはならぬのである。そこで今回は「皮膚のハリ」や「重力」を気にしながら、「オッパイのたるみ・形状」について考えてみることにした。
さて、一体バストの形状というものはどうなっているのだろう?これまでの「オッパイ星人の力学」では
- 半球モデル
- 円錐モデル
そしてもちろん、このモデルに対して不満を持つのは私だけではなくて「これらのモデルには私は納得できません。」というメールがたくさん送られてきた。それどころか、「本当のオッパイをあなたは知らないのではないですか?」という実に失礼?なメールさえ送られて来ていたのである。「それでは、参考までに本当のオッパイの資料でも送って頂けないでしょうか?」とは私は大人なので返事をしなかったが、ちゃんとしたモデルを作らないことにはこれからもそんなメールがまだまだ来るに違いないのだ。
というわけで、今回は新しいバストの形状モデルを提唱してみたい。それは「バストの内部は液体に満ちていて、その液体を外側の皮膚が支える」という
- 水風船バストモデル
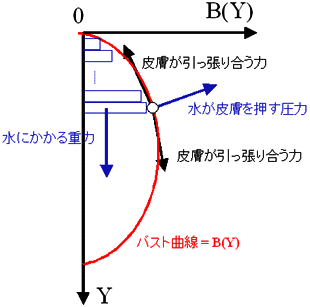
こんなモデルに基づいて、バストの形状を計算するにはどのように考えれば良いだろうか?次の図が「水風船バストモデル」における内部の水と各皮膚部分にかかる力を示してみたものである。これはバストの断面をを鉛直方向に示しており、左の黒い鉛直線が胸板であり、赤い線がバストの形状を示すバスト曲線である。(ちなみに、今回はバストを二次元の断面でのみ考えている。)
赤い線がバストの形状を示すバスト曲線
|
「水風船バストモデル」における内部の水には重力がかかり、バストの下の方にいくほど圧力がかかっている。そして、皮膚に面している内部の水はその圧力を皮膚に伝える。そして、皮膚はその圧力で変形しながら水で満ちたバストを支えるのである。この時、バストの形状= 皮膚の形状を示すバスト曲線はどんな条件を満たしているだろうか?
ここで、胸板にそって下向きにY軸をとり、バスト曲線をB(Y)で表すことにしよう。上の図をよく眺めるとわかると思うのだが、バストの形状= 皮膚の形状を示すバスト曲線をB(y)とすると、バスト曲線B(y)は実はこんな方程式を満たす。
 |
まぁ、ここでは簡単のために、係数を省略していたり、バストが本当に垂れてしまうような状況は考えていなかったりするので、ごく簡易的なバスト曲線方程式だと思って欲しい。大雑把に係数などを無視して、言葉で言ってしまえば、バスト曲線の傾きの変化はその点より上に位置するバストの重量に等しい、という感じである。自由境界におけるLaplaceの関係でも連想して頂ければわかりやすいだろうか?とにかく、この条件と適当な境界条件さえ入れてやれば、「水風船バストモデル」におけるバスト曲線B(y)は計算することができるのである。
さて、このバスト曲線方程式を一般化したり、係数をちゃんと計算したり、三次元に拡張したりということはまたいつか行うことにして、まずは適当にこのバスト曲線方程式を数値的に解いてみた。それが、例えば、次の図である。これが、「水風船バストモデル」のバストの形状の一例だ。
赤:すごくハリのあるヤングな皮膚の場合 |
この図の中でバスト形状のプロットが三種類あるのは「皮膚のハリ = 皮膚のヤング率」として三種類の値を使ってみたからだ。以前
の中でそう、もうお判りのはずだ。 「バストに関するヤング率」はまさにヤング率(Young率)なのである。実は年齢に比例する係数だったのだと書いたが、あれと同じである。今回は、年齢で変わっていくバストの皮膚のハリを「バストの皮膚のヤング率」とおいてみたのである。そういうわけで、皮膚のハリ= 皮膚のヤング率によってバストの形状は異なるわけだが、まずは眺めてみてもらいたい。以前のどうみても不自然な「半球バストモデル」等に較べて、ずっとましになっているとは思わないだろうか?特に、藍色・マゼンダのプロットなどかなり自然な形状になっていると思うのである。感受性の豊かなオッパイ星人であれば、必ずしやググッとくるハズである。
さすがに、メチャクチャ皮膚のハリがある赤色のプロットなどは松坂大輔もビックリの「超ロケット乳」になってしまっているが(といっても、この図のアスペクト比に意味はないんだけど)、今や時代は二十一世紀、宇宙へロケットで飛び出す時代だと思えば、こんな「超ロケット乳」を眺めるのもそれまた一興ではないだろうか。ぜひこの「超ロケット乳」には宇宙へ飛び出してもらいたいものである。
もちろん、世の中には「大きいことは良いことだ」という巨乳大好きオッパイ星人達もいるわけで、そんな人達のためにもう少し「大きいバスト」の場合で計算してみたものと並べて比較してみたのが次の図である。
 |
個人の好みもあると思うが、けっこう自然な「巨乳形状」が再現できている。ちなみに、今回使用した簡易的なバスト曲線方程式ではすごく巨乳だったり、皮膚のハリが無さ過ぎてあまりにバストが垂れている場合の計算はできない。簡単に言えば、Yに対してバスト曲線B(Y)が一対一対応しないためである。が、それゆえに巨乳と言っても美乳の範囲のみ考えることができるのである。
また、この「小さいバスト」の場合と「大きいバスト」の場合の比較から、「巨乳は垂れるのよっ!だから、小さい方が良いのっ!」という世の小振りなバストの女性がよく言うセリフの妥当性も確認してみたいところではなるが、そういうことは何か危険なことであるような気もしてきたので、今回は止めておきたい。
ところで、今回の話はAnti-Gravityから話が始まっているわけだが、ちなみに「水風船バストモデル」は無重力下ではどのような形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。つまり、「半球バストモデル」は「水風船バストモデル」の重力を無視した特殊な場合であり、逆に言えば「水風船バストモデル」は「半球バストモデル」にバスト内部での重力の影響を加えて一般化したものだったのである。
今回は、とりあえず新たに「水風船バストモデル」を提唱し、そのモデルにおけるバスト曲線B(y)を解くための簡易的な方程式を考察し、それを数値的に試しに解いてみた。次回は今回行った考察を用いながら、少し違うアプローチで「オッパイ星人の力学」を考えてみたいと思う。
さて、今回の話のきっかけともなった黒谷氏らの書いた本「星と生き物たちの宇宙」は原稿のごく初期の段階で実は読ませてもらっていた。その時感想を聞かれたときは、この本はメールのやりとりで構成されているので、「なるべく著者達の私的な部分を消さないままにしておいた方が面白いんじゃないか」なんて適当なことを言っていたのだった。その著者達が書いたこの本のあとがきの言葉を最後に引用して、これからの「オッパイ星人の科学」への「戒め」と「言い訳」としておきたい、と思うのだった…
科学は応用を通じて実生活に関わり、知的追求というこころの喜びにも関わる二面を持っています...多くの人に、こころを喜ばせる科学を楽しんでもらいたいですね。 H.Hirax, A.Kurotani
2001-01-16[n年前へ]
■バスト曲線その2 今日書いたメール。 
あの方程式は
>液体の圧力は水平方向ではなく表面の法線の方向に働くので
このとおり、表面の法線方向の関係に直されていますし、それが「自由境界におけるLaplace の関係」そのものですよね。
>というのは液体の圧力は水平方向ではなく表面の法線の方向に働くので、
>ヤング率が大きくなる程半球に近付くはずです。
単に液体の自由境界を計算するときと同じように解けば、あの文章の末尾に
>ちなみに「水風船バストモデル」は無重力下ではどのような
>形状をとるかと言えば、当然体積に対して表面積が最小となる「半球形状」になる。
と書いたように仰るとおり半球に近づくように一見思えます。
ここで無重力下というのは、皮膚の張力が重力に較べて十分大きい、ということなわけで「ヤング率が大きくなる」のと同じなわけです。
ところがところが、です。
「あの方程式を解くときの境界条件は胸板側の長さ・バストの体積を先に決めています。」
また、「あの座標軸の下で方程式を解く」ために、あの方程式はY,B(Y)の一対一の対応を必要としています。それが、「バストが本当に垂れてしまうような状況は考えていなかったりするので」という前提ですね。
この二つの境界条件・前提の下で、「ヤング率が大きくなる程半球に近付くはず」が本当に正しいかどうか、考えてみては如何でしょうか?
この二つの条件を除外しようとすると、方程式を作って解くのがとたんにメンドーになります。
というわけで、一般化されたバスト方程式をぜひ作って解いてみて下さい。